本文主要是介绍计组01----原反补移转换与加减乘除,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
1.原反补移的转换
以n位二进制为例
1.1 表示范围
整数:
无符号数:0 ~ 2n - 1 共可表示2n个数
原码:-(2n-1-1) ~ 2n-1-1 共可以表示2n - 1个数(0有两种表示)
反码:-(2n-1-1) ~ 2n-1-1 共可以表示2n - 1个数(0有两种表示)
补码:-2n-1 ~ 2n-1-1 共可以表示2n 个数(0只有一种表示,10……0表示-2n-1)
移码:-2n-1 ~ 2n-1-1 共可以表示2n 个数(0只有一种表示,00……0表示-2n-1)
小数(无移码):
原码:-(1 - 2-(n-1)) ~ 1 - 2-(n-1) 共可以表示2n - 1个数(0有两种表示)
反码:-(1 - 2-(n-1)) ~ 1 - 2-(n-1) 共可以表示2n - 1个数(0有两种表示)
补码:-1 ~ 1 - 2-(n-1) 共可以表示2n 个数(0只有一种表示,1.0……0表示-1)
1.2 转换
整数:
正数:原反补相同,移码为补码的高位取反.
负数:反码为原码绝对值的逐位取反;补码为反码末尾+1;移码为补码的高位取反.
小数(无移码):
正数:原反补相同。
负数:反码为原码绝对值的逐位取反;补码为反码末尾+1;
负数:原码到补码 从右边第一个1开始,左边的逐位取反 (符号位不变)
补码到负补码 从右边第一个1开始,左边的逐位取反 (符号位改变)
2.加减乘除
2.1 加减法
补码(符号位参与运算):
[x + y]补 = [x]补 + [y]补
[x - y]补 = [x]补 + [-y]补
移码:
[x + y]移 = [x]移 + [y]移 - 2-(n-1) (相加高位取反)
[x - y]移 = [x]移 + [-y]移 - 2-(n-1) (相加高位取反)
[-y]移 = [[y移]]求补
2.2 乘法
原码一位乘法: x(被乘数) * y(乘数)
符号:乘数与被乘数符号的异或
计算:
例:1.1111 * 0.1111

计算方法:先加在右移,若A0为1则 + |x|,A0为0则 + 0
注:
1.符号位为单符号位。
2.右移高位一直补0.
3.D中初始全补0.
补码一位乘法: x(被乘数) * y(乘数)
布斯法
符号:乘数与被乘数符号的异或
计算:

计算方法:先加在右移,+[-x]补 +[x]补 +0
注:
1.符号位为双符号位。
2.右移高位补符号位.
3.D中初始全补0.
4.A为带一位符号位的补码.
5.A-1为附加位,初始为0.
2.3 除法
原码除法:
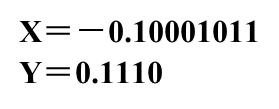

恢复余数法
左移 减 左移 减 【加 左移】(若不够减) 左移 减
加减交替法
左移 减 左移 减 【左移 加】(若不够减) 左移 减
这篇关于计组01----原反补移转换与加减乘除的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







