[论文笔记] UniFormer UniFormerV2

UniFormer & UniFormerV2 论文笔记

Author: Sijin Yu

1. Information

• Uniformer

标题: UniFormer: Unified Transformer for Efficient Spatiotemporal Representation Learning

arXiv URL: https://arxiv.org/abs/2201.04676

code: https://github.com/Sense-X/UniFormer

期刊/会议: ICLR2022

发表时间: 2022 年 01 月

• UniformerV2

标题: UniFormerV2: Spatiotemporal Learning by Arming Image ViTs with Video UniFormer

arXiv URL: https://arxiv.org/abs/2211.09552

code: https://github.com/OpenGVLab/UniFormerV2

期刊/会议: ICCV2023

发表时间: 2022 年 11 月

2. Abstract (UniFormer)

• 在高维的视频中学习丰富的时空特征表示具有挑战性, 因为在视频的每帧之间, 存在大量的局部冗余和复杂的全局冗余.

• 关于此, 最近的主流框架有: 3D CNNs 和 ViTs.

• 3D CNNs 可以高效地整合局部内容, 以降低局部冗余, 但是因为其感受野有限, 无法降低全局冗余.

• ViTs 可以通过自注意力机制降低全局冗余, 但是因为其盲目地比较所有 tokens, 无法降低局部冗余.

• 我们提出一种新式框架 Unified transFormer (UniFormer), 集成了 CNN 和 ViT 的优点, 并且在计算消耗和正确率之间取得了很好的平衡.

• 与传统的 transfomers 不同, 通过在浅层和深层分别学习局部和全局 token affinity [⚠️注: token affinity (词单元亲和力) 度量了两个 token 之间的关联性], 我们的 relation aggregator (关系聚合器) 可以同时处理时空冗余和依赖关系.

• 我们在主要的 video benchmarks 上做了实验. 在只用 ImageNet-1k 预训练的情况下, UniFormer 在 Kinetics-400 上获得了 82.9% 的准确率, 在 Kinetics-600 上获得了 84.8% 的准确率, 同时需要的 GELOPs 比其它 sota 模型少了 10 倍 [⚠️注: GELOP 指每秒十亿次浮点运算]. UniFormer 在 Something-Something V1 上获得了 60.9% 的正确率, 在 Something-Something V2 上获得了 71.2% 的正确率.

3. Methods (UniFormer)

3.1 Overview

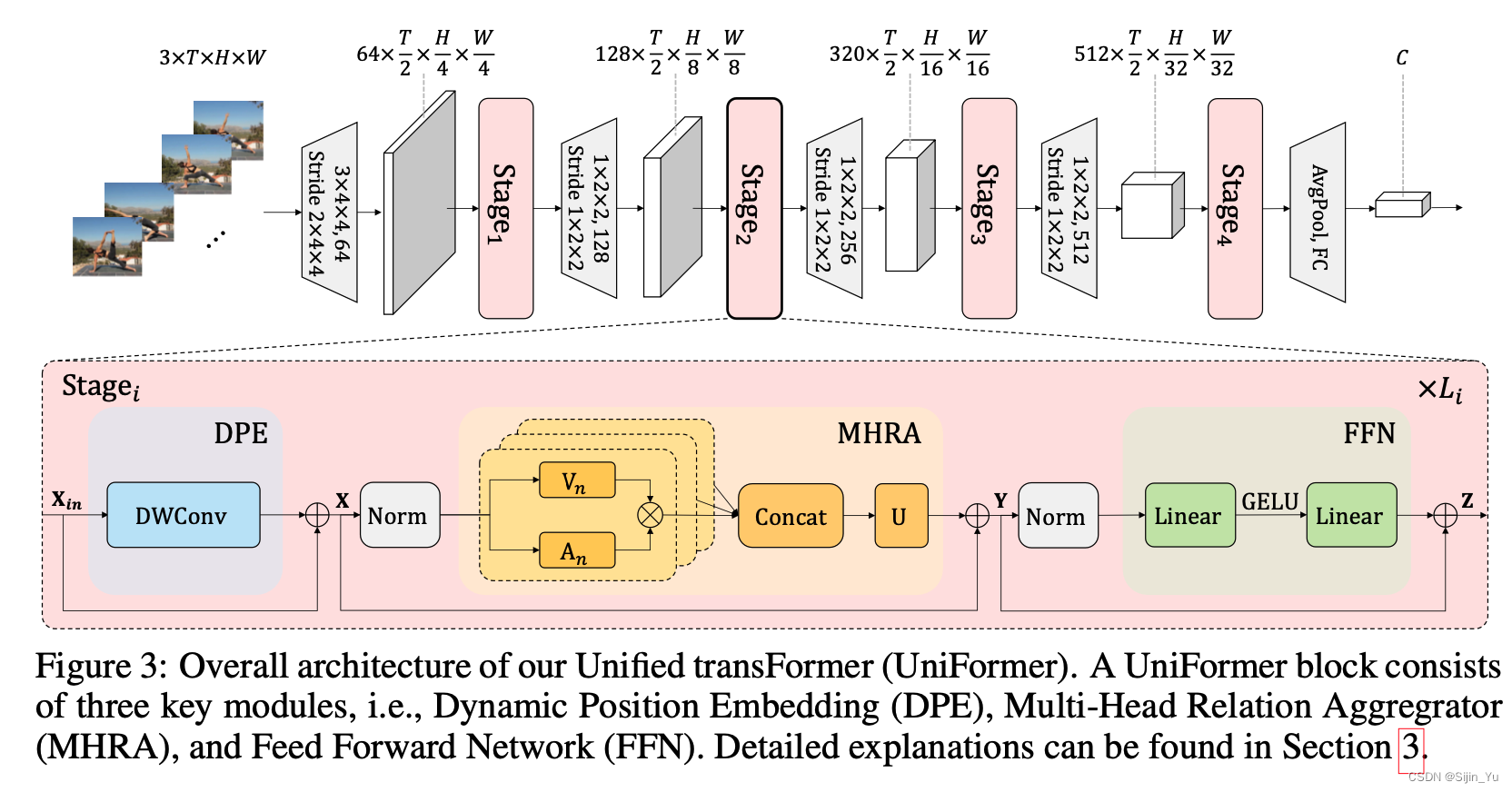
• 由 CNN 层 (灰色梯形) 和 transformer 层 (粉色圆角矩形) 组成.

• 一个 transformer 层 (Stage) 由若干个 UniFormer 块组成.

• 一个 UniFormer 块包含三个主要模块:

  • DPE: Dynamic Position Embedding, 动态位置嵌入.
  • MHRA: Multi-Head Relation Aggregator, 多头关系聚合器.
  • FFN: Feed Forward Network, 全连接层.

  具体为:
  $$\text{X}=\text{DPE}({\text{X}}_{in})+{\text{X}}_{in}\text{\hspace{1em}(1)}$$

  $$\text{Y}=\text{MHRA}(\text{Norm}(\text{X}))+\text{X}\text{\hspace{1em}(2)}$$

  $$\text{Z}=\text{FFN}(\text{Norm}(\text{Y}))+\text{Y}\text{\hspace{1em}(3)}$$

  其中, ${\text{X}}_{in}\in {\mathbb{R}}^{3\times T\times H\times W}$.

3.2 Dynamic Position Embedding (DPE)

$$\text{DPE}({\text{X}}_{in})=\text{DWConv}({\text{X}}_{in})\text{\hspace{1em}(4)}$$

$\text{DWConv}(\cdot )$ 是 0 填充的简单 3D depthwise 卷积.它的输出不改变

3.3 Multi-Head Relation Aggregator (MHRA)

• 给定一层的输入张量: $\text{X}\in {\mathbb{R}}^{C\times T\times H\times W}$.

• 将其 reshape 成一个 tokens 的序列: $\text{X}\in {\mathbb{R}}^{L\times C}$. 这里 $L=T\times H\times W$.

• 一层 MHRA 有 $N$ 个 Relation Aggregator (RA). (即 $N$ 头). 以 $R_n(\cdot )$ 指代第 $n$ 个.

• 在一个 $R_n(\cdot )$ 里的行为:
  $$R_n(\text{X})=A_n{V}_n(\text{X})\in {\mathbb{R}}^{L\times \frac{C}{N}}\text{\hspace{1em}(5)}$$

  • $V_n(\cdot )$ 是一个全连接层, 输出形状是 ${\mathbb{R}}^{L\times \frac{C}{N}}$.

  • $A_n\in {\mathbb{R}}^{L\times L}$ 表示 token affinity (词单元亲和力). 它在浅层时用于提取局部亲和力, 在深层时用于提取全局亲和力. 即: MHRA 分为 Local MHRA 和 Global MHRA.

    对于 Local MHRA:

    • 对于 tokens 序列 $\text{X}\in {\mathbb{R}}^{L\times C}$, 写成 $\text{X}=[{\text{X}}_1,\cdots ,{\text{X}}_L{]}^T$, 其中 ${\text{X}}_i\in {\mathbb{R}}^{1\times C}$ 是一个 token.

    • $A_n\in {\mathbb{R}}^{L\times L}$ 是一个矩阵, 其第 $i$ 行、第 $j$ 列的元素 (即 index 为 $(i,j)$ 的元素) 是 tokens 序列 $\text{X}$ 中的 ${\text{X}}_i$ 和 ${\text{X}}_j$ 之间的时空亲和力. 这里记作: $A_n^{local}({\text{X}}_i,{\text{X}}_j)$.

    • 给定一个 token ${\text{X}}_i$, 可以确定一个关于它的长方体 ${\Omega }_i^{t_i\times h_i\times w_i}$. 这个长方体度量了它计算局部亲和力的感受野. 具体地:
      $$t_i=\lfloor \frac{i}{H\times W}\rfloor \text{\hspace{1em}(6)}$$

      $$h_i=\lfloor \frac{i-t_i\times H\times W}{W}\rfloor \text{\hspace{1em}(7)}$$

      $$w_i=(i-t_i\times H\times W)\mathrm{mod}W\text{\hspace{1em}(8)}$$

      这里本质上是为了保证:

      给定一个目标 token ${\text{X}}_i$, 任何一个在它感受野 ${\Omega }_i^{t_i,h_i,w_i}$ 内的邻居 token ${\text{X}}_j$ 应满足:
      $$|t_i-t_j|\le \frac{t}{2}\text{\hspace{1em}(9)}$$

      $$|h_i-h_j|\le \frac{h}{2}\text{\hspace{1em}(10)}$$

      $$|w_i-w_j|\le \frac{w}{2}\text{\hspace{1em}(11)}$$

    • 令 $a_n\in {\mathbb{R}}^{t\times h\times w}$ 为可学习参数, 则

      对于在 ${\text{X}}_i$ 感受野 ${\Omega }_i^{t_i\times h_i\times w_i}$ 内的 ${\text{X}}_j$:
      $$A_n^{local}({\text{X}}_i,{\text{X}}_j)=a_n[t_i-t_j,h_i-h_j,w_i-w_j]\text{\hspace{1em}(12)}$$
      对于不在 ${\text{X}}_i$ 感受野 ${\Omega }_i^{t_i\times h_i\times w_i}$ 内的 ${\text{X}}_j$:
      $$A_n^{local}({\text{X}}_i,{\text{X}}_j)=0\text{\hspace{1em}(13)}$$

    对于 Global MHRA:

    • 矩阵 $A_n\in {\mathbb{R}}^{L\times L}$ 的 index 为 $(i,j)$ 的元素由 $A_n^{global}({\text{X}}_i,{\text{X}}_j)$ 计算.

    • 对于 Global 情况, 感受野变为 ${\Omega }^{T\times H\times W}$.

    • $Q_n(\cdot )$ 和 $K_n(\cdot )$ 是两个不同的全连接层, 类似自注意力中的存在. 它们将 ${\mathbb{R}}^C$ 映射为 ${\mathbb{R}}^{hidden}$. $hidden$ 是超参数.

    • $A_n^{global}({\text{X}}_i,{\text{X}}_j)$ 的计算规则为
      $$A_n^{global}({\text{X}}_i,{\text{X}}_j)=\frac{\exp \left(Q_n({\text{X}}_i{)}^T{K}_n({\text{X}}_j)\right)}{{\sum }_{j^{\prime }\in {\Omega }^{T\times H\times W}}\exp \left(Q_n({\text{X}}_i{)}^T{K}_n({\text{X}}_{j^{\prime }})\right)}\text{\hspace{1em}(14)}$$

• 最后, MHRA 层的行为是:
  $$\text{MHRA}(\text{X})=\text{Concat}(R_1(\text{X});R_2(\text{X});\cdots ;R_N(\text{X}))U\text{\hspace{1em}(15)}$$
  其中, $U\in {\mathbb{R}}^{C\times C}$ 是可学习的融合矩阵.

4. Experiment & Result (UniFormer)

4.1 和 SOTA 的对比

下图: 在 Kinetics-400 和 Kinetics-600 上的对比, 以低计算代价达到 SOTA 性能.

下图: 在 Something-Something V1 和 Something-Something V2 上达到 SOTA.

下图: 在计算代价和准确率之间的平衡. (横轴: 计算代价, 纵轴: 准确率)

4.2 消融实验

下图: 消融实验.

• Unified 表示是否使用 local MHRA, Joint 表示是否使用 global MHRA, DPE 表示是否使用 DPE. ✖️ 表示使用 MobileNet 块.
• Type 中的 L/G 表示四层 Stage 分别使用 Local MHRA 还是 Global MHRA.

下图: Local MHRA 中 长方体感受野的敏感性.

下图: 迁移学习的能力. 在 K400 上训练, 在 SSV1 上测试.

下图: 采样方法的敏感性. (帧数 $\times$ 时间步)

下图: Multi-clip/crop 实验.

[⚠️注: Multi-clip 指将视频按不同帧切分为多个视频, 对每个视频做分类, 然后将预测结果组合起来获得最终预测结果. Multi-clop 指将每一帧裁剪为不同的区域, 分别得到不同的多个视频, 然后将各视频的预测结果组合起来获得最终预测结果]

5. Conclusion (UniFormer)

主要创新点:

• 将 CNN 和 ViT 融合.
• 设计了 token 亲和力 $A_n$, 与自注意力有异曲同工之妙. 解决了自注意力机制盲目比较所有 token 的问题.

主要成果:

• 能同时处理局部冗余和全局冗余.
• 计算代价相对小.

6. Abstract (UniFormerV2)

• 学习具有区分性的时空特征表示是视频理解的关键问题.
• ViTs 通过自注意力展现了他们在学习长视频依赖性上的强大能力. 但不幸的是, 因为它们盲目地比较所有 tokens, 在处理局部视频冗余问题上展现出局限性.
• UniFormer 通过在 transformer 架构中整合 CNNs 和自注意力为关系聚合器 (relation aggregator), 成功地缓解了这一问题.
• 但是 UniFormer 在视频微调之前, 需要复杂的图像预训练步骤. 这限制了它的广泛应用.
• 与之相反, 大量开源的 ViTs 已经在丰富的图像监督下预训练.
• 基于这些观察, 我们通过结合预训练的 ViTs 和 UniFormer, 提出一种搭建强大视频网络族的通用范式. 我们称之为 UniFormerV2.
• 它包含了全新的 local 和 global aggregators, 并且通过集成 ViTs 和 Uniformer 的优点, 在计算代价和准确率上取得很好的平衡.
• UniFormerV2 在 8 个主流的视频 benchmarks 上获得了 SOTA 性能, 包括 K400/600/700 和 SSV1/V2. 它是第一个在 Kinetics-400 数据集上获得 90% top-1 准确率的模型.

7. Model (UniFormerV2)

7.1 Overview

• 动机: UniFormer 和 ViT 的对比

  

  • $L$ 是 Local MHRA, $G$ 是 Global MHRA, $T$ 是 Temporal MHSA.
  • SL 是有监督学习, CL 是对比学习, MIM 是 Mask Image Modeling.
  • ViTs 在图像预处理方面有优势, 而 UniFormer 在视频微调方面有优势.
  • 本模型旨在融合 ViTs 和 UniFormer 的优势.

• UniFormerV2 模型的设计和与 SOTA 的对比
  

  比起 ViTs 的主要改进:

  • 将 Temporal MHSA 改为 Loacl MHRA.
  • 将 ViT 层的输出传给 Global MHRA 并将它们在最后融合.

下图: 模型框架.

7.2 Local UniBlock

Local UniBlock 的行为:
$${\text{X}}^T=\text{LT\_MHRA}(\text{Norm}({\text{X}}^{in}))+{\text{X}}^{in}\text{\hspace{1em}(16)}$$
其中, $\text{LT\_MHRA}(\cdot )$ 表示使用局部亲和力的 MHRA. 即 $A_n({\text{X}}_i,{\text{X}}_j)$ 的计算方式为式 (12) (13).
$${\text{X}}^S=\text{GS\_MHRA}(\text{Norm}({\text{X}}^T))+{\text{X}}^T\text{\hspace{1em}(17)}$$
其中, $\text{GS\_MHRA}(\cdot )$ 表示使用全局亲和力的 MHRA. 即 $A_n({\text{X}}_i,{\text{X}}_j)$ 的计算方式为式 (14).
$${\text{X}}^L=\text{FFN}(\text{Norm}({\text{X}}^S))+{\text{X}}^S\text{\hspace{1em}(18)}$$
[⚠️注: 留意到, Local UniBlock 的输入和输出形状是完全一样的.]

7.3 Global UniBlock

Global UniBlock 的行为:
$${\text{X}}^C=\text{DPE}({\text{X}}^L)+{\text{X}}^L\text{\hspace{1em}(19)}$$
其中, $\text{DPE}(\cdot )$ 是 Dynamic Position Embedding, 同式 (4).
$${\text{X}}^{ST}=\text{C\_MHRA}(\text{Norm}(\text{q}),\text{Norm}({\text{X}}^C))\text{\hspace{1em}(20)}$$
其中, $\text{C\_MHRA}(\text{q},\cdot )$ 是互注意力风格的 MHRA. 它的第 $n$ 个关系聚合器头 (Relation Aggregator) $R_n^C(\text{q},\cdot )$ 表示如下, 其中 $\text{q}\in {\mathbb{R}}^{1\times C}$ 是一个可学习的 query. [⚠️注: $\text{q}$ 的迭代和 Multi-stage Fusion 模块有关]
$$R_n^C(\text{q},\text{X})=A_n^C(\text{q},\text{X})V_n(\text{X})\text{\hspace{1em}(21)}$$
其中, $A_n^C(\text{q},\text{X})$ 是互注意力亲和力矩阵, 用于学习 $\text{q}$ 和 $\text{X}$ 的关系.其计算如下:
$$A_n^C(\text{q},{\text{X}}_j)=\frac{\exp \left(Q_n(\text{q}{)}^T{K}_n({\text{X}}_j)\right)}{{\sum }_{j^{\prime }\in {\Omega }^{T\times H\times W}}\exp \left(Q_n(\text{q}{)}^T{K}_n({\text{X}}_{j^{\prime }})\right)}\text{\hspace{1em}(22)}$$
其中, $V_n(\cdot )$, $Q_n(\cdot )$, $K_n(\cdot )$ 都是全连接层.

同式 (15), $\text{C\_MHRA}(\text{q},\cdot )$ 的计算为:
$$\text{C\_MHRA}(\text{q},\text{X})=\text{Concat}(R_1^C(\text{q},\text{X});R_2^C(\text{q},\text{X});\cdots ;R_N^C(\text{q},\text{X}))U\text{\hspace{1em}(23)}$$
最后, 计算 ${\text{X}}^G$:
$${\text{X}}^G=\text{FFN}(\text{Norm}({\text{X}}^{ST}))+{\text{X}}^{ST}\text{\hspace{1em}(25)}$$

7.4 Multi-stage Fusion

这一模块的任务: 将 Local UniBlock 输出的 ${\text{X}}^L$ 和 Global UniBlock 输出的 ${\text{X}}^G$ 融合, 并更新 query $\text{q}$. 下图: 四种设计思路

记第 $i$ 个 Global UniBlock 的输出为 ${\text{X}}_i^G=G_i({\text{q}}_i,{\text{X}}_i^L)$.

• Sequential 方式: 更新 ${\text{q}}_i$ 为上一个 Global UniBlock 的输出, 即:
  $${\text{q}}_1\leftarrow \text{Random}()$$

  $${\text{q}}_i={\text{X}}_{i-1}^G$$

  $${\text{X}}_i^G=G_i({\text{q}}_i,{\text{X}}_i^L)=G_i({\text{X}}_{i-1}^G,{\text{X}}_i^G)$$

  $$\text{F}={\text{X}}_N^G$$

• Parallel 方式: 随机初始化所有的 ${\text{q}}_i$, concat 所有 ${\text{X}}_i^G$ 并映射到对应的形状, 即:
  $${\text{q}}_1,{\text{q}}_2,\cdots ,{\text{q}}_N\leftarrow \text{Random}()$$

  $${\text{X}}_i^G=G_i({\text{q}}_i,{\text{X}}_i^L)$$

  $$\text{F}=\text{Concat}({\text{X}}_1^G;{\text{X}}_2^G;\cdots ;{\text{X}}_N^G)U^F$$

  其中, $U^F\in {\mathbb{R}}^{N\times C}$ 是可学习的.

• Hierarchical KV 方式: 随机初始化所有的 ${\text{q}}_i$, 但将上一个 Global UniBlock 的输出作为当前 Global UniBlock 的输入之一, 即:
  $${\text{q}}_1,{\text{q}}_2,\cdots ,{\text{q}}_N\leftarrow \text{Random}()$$

  $${\text{X}}_i^G=G_i({\text{q}}_i,[{\text{X}}_{i-1}^G,{\text{X}}_i^L])$$

  $$\text{F}={\text{X}}_N^G$$

• Hierarchical Q 方式: 随机初始化所有的 ${\text{q}}_i$, 但将上一个 Global UniBlock 的输出作为当前 Global UniBlock 的 $\text{q}$ 之一, 即:
  $${\text{q}}_1,{\text{q}}_2,\cdots ,{\text{q}}_N\leftarrow \text{Random}()$$

  $${\text{X}}_i^G=G_i(\text{[}{\text{X}}_{i-1}^G,q_i],{\text{X}}_i^L])$$

  $$\text{F}={\text{X}}_N^G$$

实验表明, Sequential 方式和 Hierarchical Q 方式最有效 (见消融实验部分), 模型采用 Sequential 方式作为基准.

8. Experiment & Result (UniFormerV2)

8.1 和 SOTA 的对比

下图: 在 K400 上的性能比较.

下图: 在 K600/700 上的性能比较.

下图: 在 MiT V1 上的性能比较.

下图: 在 SSV2 上的性能比较.

原文在 SSV1, ActivityNet, HACS 上也做了实验, 均达到了 SOTA.

8.2 消融实验

9. Conclusion (UniFormerV2)

主要创新点:

• 将 UniFormer 的设计放入 ViT 框架中.
• 为 ${\text{X}}^G$ 的融合设计了四种方式.

10. 总结

UniFormer 设计了多头关系聚合器 (MHRA), 很好地处理了视频数据的局部冗余和全局冗余; UniFormerV2 在此基础上, 将 UniFormer 中大获成功的 MHRA 设计成块, 设计了 Local UniBlock 和 Global UniBlock, 并且设计了 Global Cross MHRA, 在 Multi-stage Fusion 中提出四种方式, 结合了 ViTs 的优点, 大大提高了视频理解的性能.