CGCS2000、WGS84和ITRF框架坐标之间的差异和转换方法

本文主要是介绍CGCS2000、WGS84和ITRF框架坐标之间的差异和转换方法，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

2000国家大地坐标系（简称为CGCS2000）是我国最新的国家大地坐标系统，于2008年7月1日在我国正式启用，其优越性已逐步得到体现。WGS84坐标系是美国国防部制图局建立起的坐标系，从建立之初到现在经过了四次精化，并在后三次精化中与ITRF相应的框架和历元对齐。

CGCS2000采用的ITRF97框架、2000.0历元的三维地心坐标系统，地球上的板体是在不断运动的，不同时刻位于地球不同板块上站点的实际位置在不断变化，因此同一个地点，当下的位置会与CGCS2000基准时刻的位置不同。如基于当前的ITRF97框架、2009历元坐标值与CGCS2000坐标的相比，最大差0.6m。

随着CGCS2000坐标系的广泛应用，在实际生产当中，我们经常用到WGS84与CGCS2000以及其他ITRF框架之间的坐标转换,本文通过详细介绍ITRF框架以及对这两种坐标系的定义、实现方法及相互关系，指出这两种坐标系之间的差异和ITRF框架之间的转换问题

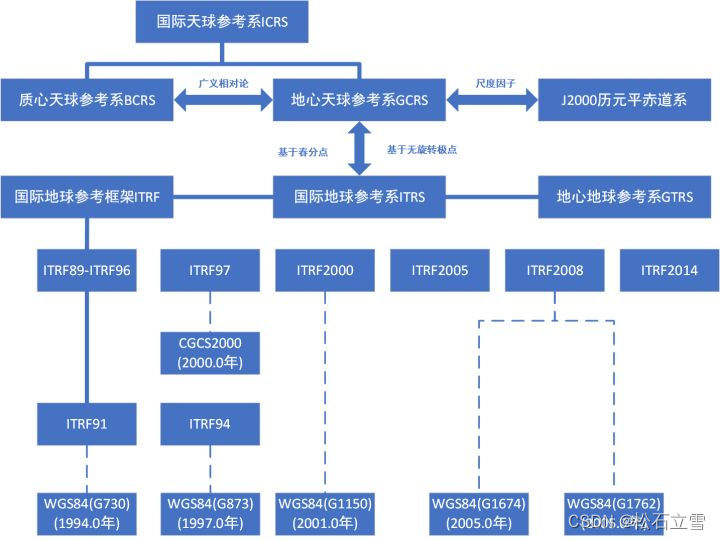
ITRF框架

地球形状每时每刻都在变化。研究地球板块的运行时，需要一个参考框架用于表述其运动情况。国际地面参考系统（International Terrestrial Reference System，ITRS）描述了如何创建适合使用的参考系应用于地球表面或接近表面的测量过程。这是以很多的物理标准做为叙述，创建出一组可能的现实化标准的相同过程。ITRS定义了一个大地测量的座标系统，作为SI的测量系统。国际地球参考系（Internationa Terrestrial Reference Frame, ITRF）是国际地表参考系统的实现，其综合地表上一组观测点的坐标信息而形成。

基于ITRF，可以用于研究地球的板块构造、区域沉降或负载，或者在研究宇宙中地球旋转时用于描述地球。地球的旋转是在基于恒星建立的天体参考框架（International Celestial Reference Frame，ICRF）中测量的。ITRF和ICRF之间的关系就是地球方向参数（Earth Orientation Parameters, EOP）.ITRF和ICRF为比较不同地点的观测和结果提供了一个共同的参考。

目前，四种主要的大地测量技术全球导航卫星系统（Global Navigation Satellite System，GNSS）、甚长基线干涉（Very Long Baseline interferometry, VLBI）、卫星激光测距（Satellite Laser ranging, SLR）多普勒卫星跟踪和无线电定位系统（DORIS），然而这四种技术均无法单独提供完整的参考框架参数，因此ITRF综合四种技术的优点，提供了当前最为准确的地球参考框架。

ITRS定义为

1）原点为地心，并且是指包括海洋和大气在内的整个地球的质心。
2）长度单位为米（m），并且是在广义相对论框架下定义。
3）Z轴从地心指向BIH（国际时间局）1984.0定义的协议地球极(Conventional Terrestrial Pole，CTP)。
4）X轴从地心指向BIH1984.0定义的零度子午面（BIH Zero Meridian）和CTP赤道的交点。
5）Y轴与XOZ平面垂直而构成右手坐标系。
6）时间演变基准是使用满足无整体旋转NNR条件的板块运动模型，用于描述地球各块体随时间的变化。

IERS每年将全球站的观测数据进行综合处理和分析，得到一个ITRF框架，并以IERS年报和IERS技术备忘录的形式发布。现已发布的ITRF系列有ITRF88、ITRF89、ITRF90、ITRF91、ITRF92、ITRF93、ITRF94、ITRF96、ITRF2000、ITRF2005、ITRF2008，ITRF2014和ITRF2020全球参考框架。

CGCS2000坐标系

2000国家大地坐标系，是我国当前最新的国家大地坐标系，英文名称为China Geodetic Coordinate System 2000，英文缩写为CGCS2000。CGCS2000的实现精度是：在参考历元2000.0，水平坐标与高程坐标的精度分别好于1cm和3cm，水平速度的精度约3mm/a。

CGCS2000采用ITRF97框架，历元为2000.0，投影方式多采用高斯-克吕格投影。国家大地坐标系的定义包括坐标系的原点、三个坐标轴的指向、尺度以及地球椭球的4个基本参数的定义。

原点为包括海洋和大气的整个地球的质量中心；
Z轴由原点指向历元2000.0的地球参考极的方向，该历元的指向由国际时间局给定的历元为1984.0的初始指向推算，定向的时间演化保证相对于地壳不产生残余的全球旋转，
X轴由原点指向格林尼治参考子午线与地球赤道面（历元2000.0）的交点，
Y轴与Z轴、X轴构成右手正交坐标系。
采用广义相对论意义下的尺度。
地球椭球参数如下

参数名	标记符号	数值	单位
长半轴	a	6378137	m
扁率	1/f	298.257222101	-
地心引力常数	GM	3.986004418 *10¹⁴	m³/s²
自转角速度	ω	7.292115 *10^-5	rad/s
短半轴	b	6356752.31414	m
极曲率半径	c	6399593.62586	m
第一偏心率	e	0.0818191910428	-

WGS84坐标系

WGS84是为GPS全球定位系统使用而建立的坐标系统。其初次WGS84的精度为1～2cm，由全球地心参考框架、地球重力场模型、WGS84水准面等组成，主要由NGA(美国国家智能化地理空间局)负责维护。

WGS84的坐标原点为地球质心
Z轴指向BIH（国际时间服务机构）1984.0定义的协议地球极（CTP)方向
X轴指向BIH1984.0的零子午面和CTP赤道的交点
Y轴与Z轴、X轴垂直构成右手坐标系。
其地球椭球参数为（仅扁率与CGCS2000不同）

参数名	标记符号	数值	单位
长半轴	a	6378137.0	m
扁率	1/f	298.257223563	-
地心引力常数	GM	3.986004418 *10¹⁴	m³/s²
自转角速度	ω	7.292115 *10^-5	rad/s

通过遍布世界的卫星观测站观测到的坐标建立，其初次WGS84的精度为1-2m，之后经过5次实现，精度原来越高：

1）WGS84(G730)，1994年6月29日，精度~10cm，对应ITRF91，历元1994.0，10站；
2）WGS84(G873)，1997年1月29日，精度~5cm，对应ITRF94，历元1997.0，12站；
3）WGS84(G1150)，2002年1月20日，精度~1cm，对应ITRF2000，历元2001.0，26站；
4）WGS84(G1674)，2012年2月8日，精度<1cm，对应ITRF2008，历元2005.0；
5）WGS84(G1762)，2013年10月16日，精度<1cm，对应ITRF2008，历元2005.0。
6）WGS84(G2139)，2021年1月3号

在这里插入图片描述二者扁率变化引起的变化：

扁率变化df不引起大地经度变化；
扁率变化df引起大地纬度的变化范围为0(赤道和两极至0.105mm(B＝45°)；
扁率变化df引起大地高的变化范围为0(赤道)到0.105mm(两极)；
扁率变化df引起椭球面上正常重力变化范围为0(两极)到0.016×10-8ms-2(赤道)。

不同测站不同框架不同历元坐标对比（单位：m）
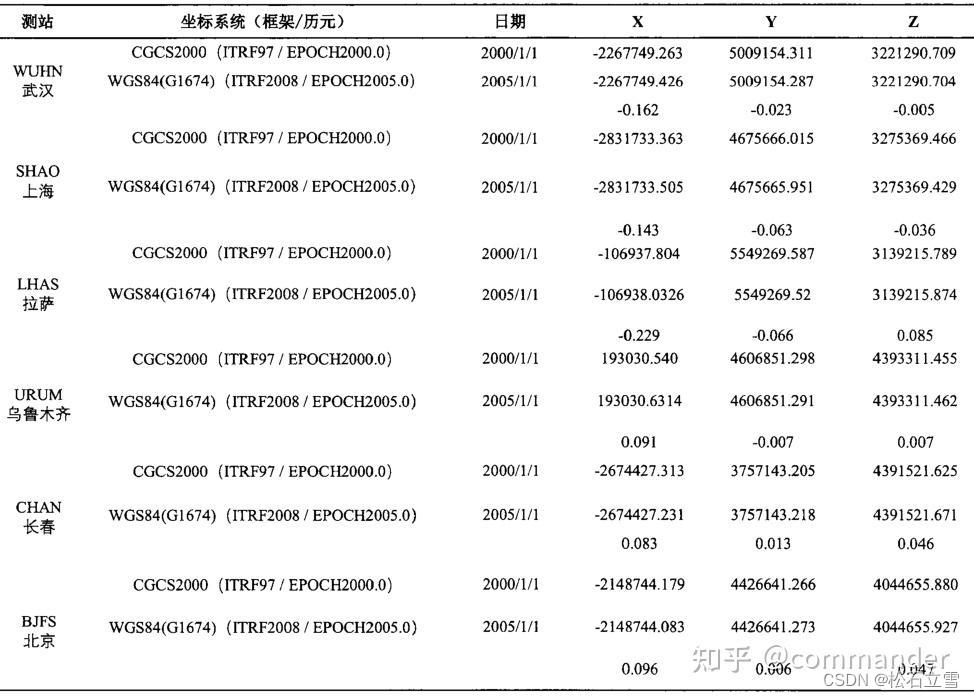
在这里插入图片描述

ITRF框架之间的转换和历元归算

由于不同的观测历元以及各ITRF框架参数不尽相同，因此相同点在每个ITRF之间的坐标也有差别，这就需要进行测站坐标的历元归算和ITRF框架之间的坐标转换。

转换的标准关系是七个参数的欧几里得相似性：三个平移分量、一个缩放因子和三个旋转角，分别指定为T1，T2，T3，D，R1，R2，R3，其一阶微分形式分别为 $\dot T1，\dot T2，\dot T3，\dot D，\dot R1，\dot R2，\dot R3$ ；

X1和X2分别是目标框架和原框架下的三维坐标，二者之间的关系遵循以下方程式

$X2=X1+T+DX1+RX1\\ \ \\ X1=\begin{pmatrix} x_1\\y_1\\z_1 \end{pmatrix} \ X2=\begin{pmatrix} x_2\\y_2\\z_2\end{pmatrix} \\ T=\begin{pmatrix} T1\\T2\\T3 \end{pmatrix} \ R=\begin{pmatrix} \ 0&-R3&R2\\ R3&0&-R1\\ -R2&R1&0\end{pmatrix}$

上述公式假定在给定的固定坐标系内是线性的。原点的偏移量在几百米左右，缩放和旋转的量级在 $10^{-5}$ 的水平。一般来说，X1，X2，T，D，R都是时间的函数，因此上式中的改写为微分形式为
$\dot X2=\dot X1+\dot T+\dot DX1+D\dot X1+\dot RX1+R\dot X1$