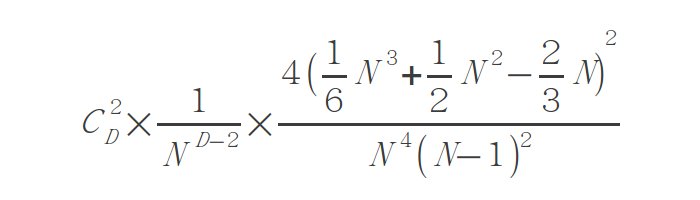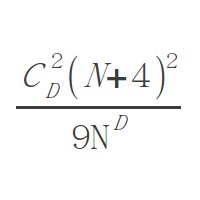本文主要是介绍【HDU】4873 ZCC Loves Intersection 数学,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
传送门:【HDU】4873 ZCC Loves Intersection
题目大意:给你一个D维的空间,每个维度都有一条线段平行与该维度属于的轴(如X,Y,Z轴),且线段的端点坐标取值范围0~N-1,保证左端点严格小于右端点(除该维度,其他维度的值两端点均相等)。现在告诉你每条线段的左右端点的坐标都是随机的,0~N-1随机到的概率是完全相等的!现在如果两条线段如果相交于一点,你可以获得一点能量。你需要回答D条线段的坐标随机后能得到的能量的期望值。
题目分析:
这次多校真的是被高中生虐惨了,也不知道怎么说,还是自己太弱了,其实怎么说呢,可能是我太懦弱了吧,总是不敢去想,到最后竟然还松懈了?!我真的是太不负责任了!唉,这题比赛的时候写不出来,其实也没怎么看,那时一直在讨论其他的题,但是却一点思路都没有= =唉唉唉。。。。
这题赛后看了下题解= =||看不懂怎么破,算了题意倒是看懂了 ,那么自己推公式吧= =||,推着推着竟然还真的出来了。。。。。只能呵呵了。。果然太弱。。。
这题赛后交上去看了下跑的时间,,,,真是出乎意料。。。C++15ms。。G++直接0ms,第一倒是有点意外。。。。
先来说说这题吧,其实如果两个线段要相交,得先满足一个前提条件:两条线段D维中必须有D-2维是相同的,多了是不行的。为什么,如果有多于2维是不同的,那么就会出现类似三维的情况(仔细想想,无法直观的描述+ —— +)。
然后我们就需要枚举剩下两维的情况了,假设该两维的坐标轴为X轴,Y轴。
那么这样平行于X轴的线段在Y=0的时候一共有N*(N-1)/2种情况((0,1),(0,2),...,(0,N-1),(1,2),(1,3),...(1,N-1),...(N-2,N-1))所以在0~N-1上平行于X轴的线段一共有N*N*(N-1)/2种,同理平行于Y轴的线段一共有N*N*(N-1)/2种,那么同时考虑两条线段的情况一共有N^4*(N-1)^2种。
现在我们假设平行于Y轴的线段Ly的包括端点Y = 0。那么平行于X轴的线段Lx有多少种情况会和该线段相交?
现在我们只考虑Lx在Y = 0时的情况数。考虑Ly包括Y = 0时在列X = 0上,那么一共有N-1一种情况((0,1),(0,2),...,(0,N-1)),如果X = 1,那么一共有(N-1) + (N-2)种情况((0,1),(0,2),...(0,N-1),(1,2),(1,3),...,(1,N-1)),如果X = 2,那么一共有2*(N-2)+(N-3)种情况((0,2),(0,3)...(0,N-1),(1,2),(1,3),...,(1,N-1),(2,3),(2,4),...,(2,N-1)),...,如果X = N-1,那么一共有(N-1)*(N-(N-1))+(N-N)种情况((0,N-1),(1,N-1),(2,N-1),...,(N-2,N-1))。
这样我们为了能得到一个通式,那么对X=0时的转化一下:N-1 = 0*(N-0)+(N-1)。
这样Ly包括Y = 0,Lx在Y = 0时的情况数cnt
=0*(N-0)+2*(N-1)+3*(N-2)+4*(N-3)+...+N*(N-(N-1))
=(2+3+4+...+N)*N-(2*1+3*2+4*3+...+N*(N-1))
=(2+N)*(N-1)*N/2-(1^2+2^2+3^2+...+(N-1)^2)-(1+2+3+...+(N-1))
有1^2+2^2+3^2+...+N^2= N*(N+1)*(2*N+1)/6
所以cnt = (N*N*N/6+N*N/2-2*N/3)*(N-1)。其中N-1是Ly 包括端点Y = 0的情况数。
同理当Lx在Y = 1时,Ly包括端点Y = 1的情况数为(N-1)+(N-2);当Lx在Y = 2时,Ly包括端点Y = 2的情况数为2*(N-2)+(N-3);...;当Lx在Y = N-1时,Ly包括端点Y = N-1的情况数为(N-1)*(N-(N-1))+(N-N)。
是不是很熟悉?
没错,所有相交的情况数就是cnt^2=((N*N*N/6+N*N/2-2*N/3)*(N-1))^2。
那么考虑多维,如果这两个线段要相交,其余D-2维必须保证相同,那么这件事情发生的概率是:(1/N)^(D-2)。
并且我们很容易知道任意两条线段发生相交的组合数为D*(D-1)/2。
至此,我们可以得到得到能量的期望值为:
化简后可得:
(顺便学习了用LibreOffice Math。。。好难玩,,要把公式搞过来不知道怎么办只能靠截图然后用图片编辑器搞过来- -”)
由于所有的数相乘会爆long long ,所以我们需要高精度,但是题目又要求我们约分,该怎么约分好呢?
我们可以将所有的乘项拆开来!然后拿分子的所有项去和分母的所有项约分,期间通过gcd得到公约数即可。
这样我们就可以对约分后的数展开高精度乘法了(我就只用高精度乘了单精度去计算了)。
如果分母都是1,那么就不用输出/和分母的1了(题目要求)。
至此,终于全部搞定(泪湿了)。。。
代码如下:
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <time.h>
#include <stdlib.h>
using namespace std ;#define REP( i , n ) for ( int i = 0 ; i < n ; ++ i )
#define REPF( i , a , b ) for ( int i = a ; i <= b ; ++ i )
#define REPV( i , a , b ) for ( int i = a ; i >= b ; -- i )
#define CLR( a , x ) memset ( a , x , sizeof a )typedef long long LL ;const int MAXN = 30005 ;
const int MAXE = 200000 ;
const int MAXQ = 200000 ;
const int INF = 0x3f3f3f3f ;
const int TOP = 1000000000 ;int N , D ;
LL a[MAXN] ;int gcd ( int a , int b ) {return a ? gcd ( b % a , a ) : b ;
}void print ( int A[] , int B[] , int only_one ) {int top ;top = 0 ;CLR ( a , 0 ) ;a[0] = 1 ;REP ( i , 4 ) {REPF ( j , 0 , top ) {a[j] *= A[i] ;if ( j && a[j - 1] >= TOP ) {a[j] += a[j - 1] / TOP ;a[j - 1] %= TOP ;}if ( a[top] >= TOP )++ top ;}}printf ( "%d" , ( int ) a[top] ) ;-- top ;REPV ( i , top , 0 )printf ( "%09d" , ( int ) a[i] ) ;if ( only_one ) {printf ( "\n" ) ;return ;}//---------------------printf ( "/" ) ;//---------------------top = 0 ;CLR ( a , 0 ) ;a[0] = 1 ;REPF ( i , 0 , D ) {REPF ( j , 0 , top ) {a[j] *= B[i] ;if ( j && a[j - 1] >= TOP ) {a[j] += a[j - 1] / TOP ;a[j - 1] %= TOP ;}if ( a[top] >= TOP )++ top ;}}printf ( "%d" , ( int ) a[top] ) ;-- top ;REPV ( i , top , 0 )printf ( "%09d" , ( int ) a[i] ) ;printf ( "\n" ) ;
}void solve () {if ( D == 1 ) {printf ( "%d\n" , 0 ) ;return ;}int A[4] = { N + 4 , N + 4 , D , D - 1 } ;int B[100] = { 18 } ;int tmp ;REPF ( i , 1 , D )B[i] = N ;REP ( i , 4 )REPF ( j , 0 , D )if ( ( tmp = gcd ( A[i] , B[j] ) ) > 1 )A[i] /= tmp , B[j] /= tmp ;int only_one = 1 ;REPF ( i , 0 , D )if ( B[i] != 1 )only_one = 0 ;print ( A , B , only_one ) ;
}int main () {while ( ~scanf ( "%d%d" , &N , &D ) )solve () ;return 0 ;
}这篇关于【HDU】4873 ZCC Loves Intersection 数学的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!