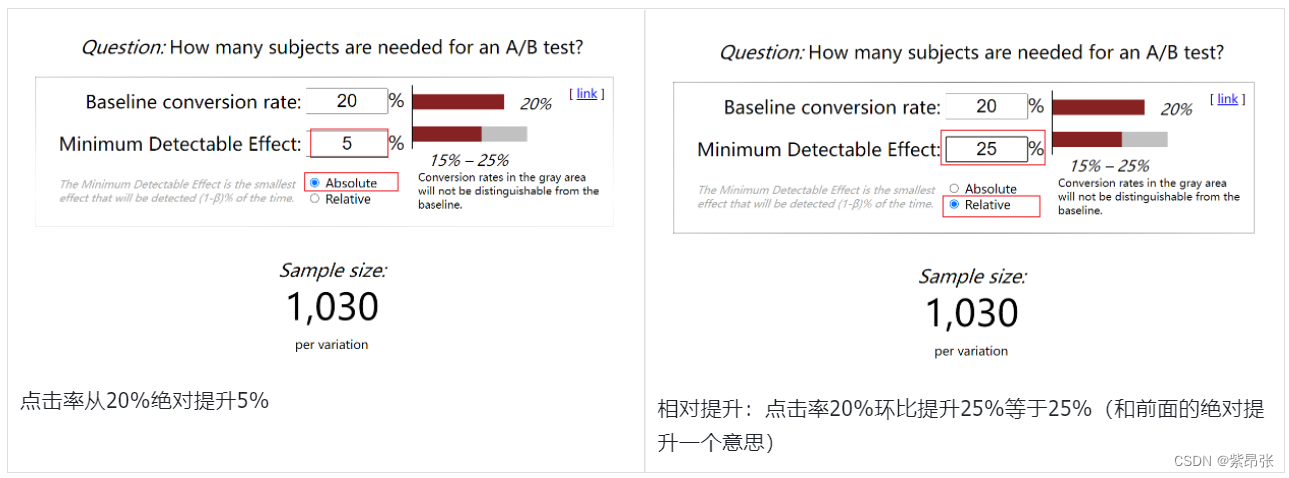
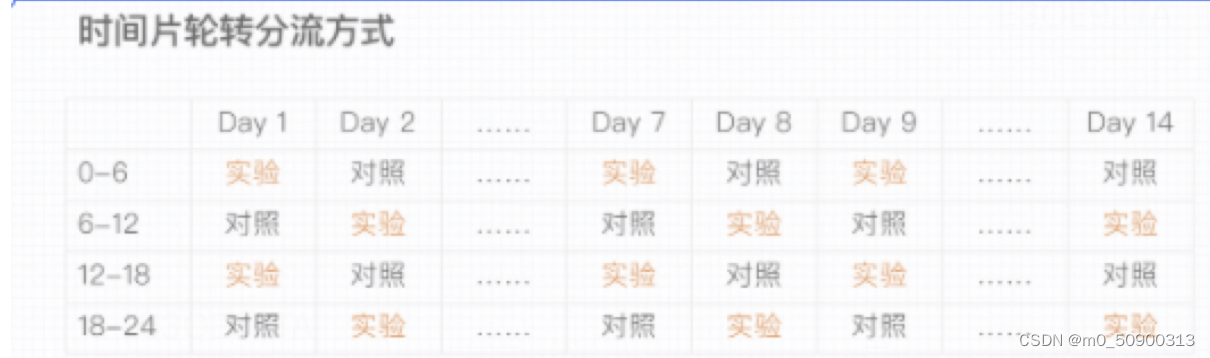
本文主要是介绍abtest,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!

公司:云眼,专门做abtest
### 简介
#
# A/B 测试是数据分析师和数据科学家需要经常完成的工作,非常重要。如果你在工作中有一些实践经验,那学习起来就会更加游刃有余。
#
# 本项目设定了一家电子商务网站运行 A/B 测试的情境。你的目标是通过这个项目来帮助公司分析和决定他们是否应该使用新的页面,保留旧的页面,或者应该将测试时间延长,之后再做出决定。
#
#### I - 概率
#
# 先导入数据。
import pandas as pd
import numpy as np
import random
import matplotlib.pyplot as plt
get_ipython().run_line_magic('matplotlib', 'inline')random.seed(42)
# `1.` 导入 `ab_data.csv` 数据,并将其存储在 `df` 中。 你可以直接进行以下问题的回答,或者 **做教室里的测试 1** 。
#
# a. 导入数据集,查看前几行数据:
df = pd.read_csv('ab_data.csv')
df.head()
# b. 查看数据集的行数。
df.count()
df.shape()# c. 查看数据集中的用户数量(不同的user_id数)。
session_counts = df['user_id'].value_counts(ascending=False)
multi_users = session_counts[session_counts > 1].count()print('There are %s users that appear multiple times in the dataset' % (multi_users))# d. 转化用户的占比。
df.converted.mean()# e. 请计算数据中 `new_page` 与 `treatment` 不匹配的次数。提示:在一个合理的实验设计里,控制组(control)
# 应该对应旧页面(old_page),实验组(treatment) 对应新页面(new_page)。#方法1
df.query('landing_page == "new_page" and group == "control"').count()[0] + df.query('landing_page == "old_page" and group == "treatment"').count()[0]#方法2
pd.crosstab(df['group'], df['landing_page'])
# 把左上和右下相加 结果和上面是一样的 # f. 是否有任何行空缺数值? 下面两种方法
df.info()
df.isnull().sum()# `2.` 对于 **treatment** 和 **new_page** 不匹配的行或 **control** 与 **old_page** 不匹配的行,我们不能确定该行是否接收到了新页面还是旧页面。如何处理这些行?你可以返回教室里的页面先做
# **测试 2** 。
#
# a. 现在,参照测试2的答案去创建一个符合要求的新数据集。将新 dataframe 存储在 **df2** 中。# 过滤出new page 和 control 的数据
npcontrol = df[(df.landing_page == "new_page") & (df.group == "control")]# 过滤出 old page 和 treatment 的数据
optreatment = df[(df.landing_page == "old_page") & (df.group == "treatment")]#合并结果集
inaccurate = pd.concat([npcontrol, optreatment])inaccurate_index = inaccurate.index# 创建df2 去掉不需要的数据
df2 = df.drop(inaccurate_index)
# 再次检查一下 上面的 3893行数据是否已被移除
df2[((df2['group'] == 'treatment') == (df2['landing_page'] == 'new_page')) == False].shape[0]# `3.` 根据 **df2** 来回答以下问题,或者做教室里的 **测试3** 。
#
# a. **df2** 中的用户数量(不同的 **user_id**) ?
df2['user_id'].nunique()
df2['landing_page'].unique()# b. **df2** 中有一个重复的 **user_id** 。它是什么?
df2[df2.duplicated('user_id')]
df2['user_id'].duplicated().sum()
# c. 这个重复 **user_id** 的行信息是什么?
df2[df2.user_id == 773192]
# d. 删除一行重复行,但仍然存储 dataframe 为 **df2**。
df2.drop(labels = 1899, axis=0, inplace=True)
df2['converted'].mean()# b. `control` 组用户的转化率是多少?
df2[df2['group'] == "control"]['converted'].mean()
# c. `treatment` 组用户的转化率是多少?
df2[df2['group'] == "treatment"]['converted'].mean()
# d. 一个用户收到新页面的概率是多少?
(df2.landing_page == "new_page").mean()
# e. 分析到这里,你是否认为有足够的数据支持来证明旧页面或者新页面可以带来更高的转化率?
#
# **在这里写出你的答案。**
根据上述比例,从治疗组和对照组转换的数值反馈出的的差异很小,因此,我们无法得出新的页面会带来更好的转化率第二部分:
#第二部分:
# ### II - A/B 测试
#
# 因为每个事件都对应有一个时间记录(time stamp 时间戳),所以技术上你可以实现每次观察都连续运行假设检验。
#
# 然而,问题的难点在于,什么时候停止你的试验:是在发现其中一组的试验效果足够好时立即停止?还是在这样的观察结果又持续发生了一段时间再停止?需要运行多长时间才能确认两个页面没有带来用户转化率的显著差异?
#
# 这些问题是 A/B 测试中最难的部分。如果你对下面提到的一些知识点比较生疏,请先回顾课程中的“描述统计学”部分的内容。# `1.` 现在,你需要根据我们提供的数据做出决策:你假设旧页面效果更佳,除非在一类错误在5%以内,新页面被证明更好。基于此,你的零假设和备择假设是什么? 你可以用文字表述或用 **$p_{old}$** 与 **$p_{new}$** (即,旧页面转化率与新页面转化率)来陈述你的假设。
#
# **在这里给出你的答案。**H 0 :p new −p old <=0
H0:pnew−pold<=0H 1 :p new −p old >0
H1:pnew−pold>0# `2.` 假定在零假设中,不管是新页面还是旧页面, $p_{new}$ 与 $p_{old}$ 都有相同的转化成功的概率,也就是说, $p_{new}$ 与 $p_{old}$ 是相等的。此外,我们还假设它们都等于**ab_data.csv** 中的 **转化率(converted)**。 <br>
#
# 现在,在新旧页面上执行抽样分布,并计算 **转化(converted)** 差异。记住,每个页面的样本大小要与 **ab_data.csv** 相同。计算零假设中10000次迭代计算的估计值。 <br>
#
# 使用下面的单元格提供这个模拟试验的内容。如果不太理解如何进行模拟,不要担心,你可以通过回答下面的问题来理清思路。同时,你可以在教室里的 **测试 5** 里验证你的答案是否正确。<br>
#
# a. 在零假设中,$p_{new}$ **转化率** 是多少?
p_new = df2['converted'].mean()
p_newp_old = df2['converted'].mean()
p_old# c. $n_{new}$ 是多少?
n_new = df2.query('group == "treatment"')['user_id'].count()
n_new = int(n_new)
n_new# d. $n_{old}$?是多少?
n_old = df2.query('group == "control"')['user_id'].count()
n_old = int(n_old)
n_old# e. 在零假设中,使用 $p_{new}$ (新页面的转化率)模拟 $n_{new}$ 个新页面的转化,并将这些 $n_{new}$ 个 1 和 0 存储
# 在 **new_page_converted** 中。new_page_converted = np.random.binomial(1, p_new, n_new)
new_page_converted
new_page_converted.shape# f. 在零假设中,使用 $p_{old}$ (旧页面的转化率)模拟 $n_{old}$ 个旧页面的转化,并将这些 $n_{old}$ 个 1 和 0 存储在 **old_page_converted** 中。# 此处尝试使用 np.random.binomial 来回答,对于不了解这个函数的同学 可以用下列代码进行熟悉使用
# 给定10次抛硬币试验,可产生10个数据点:from numpy import randomx = random.binomial(n=10, p=0.5, size=10)print(x)# 可视化binomial分布的特点
from numpy import random
import matplotlib.pyplot as plt
import seaborn as snssns.distplot(random.binomial(n=10, p=0.5, size=1000), hist=True, kde=True)plt.show()# 正态分布与二项分布之间的差异
# 主要区别在于正态分布是连续的,而二项式是离散的,
# 但是如果有足够的数据点,它将与具有特定位置和范围的正态分布非常相似。# 在本例中只有 0和 1 两种情况 所以用二项分布功能
old_page_converted = np.random.binomial(1, p_old,n_old)
old_page_converted# g. 根据 e 和 f,计算 $p_{new}$ 和 $p_{old}$ 的差异值($p_{new}$ - $p_{old}$)。# h. 由于单个数值不能形成分布图形,请参考以上a-g的过程,模拟 10,000 个 $p_{new}$ 与 $p_{old}$ 差异值($p_{new}$ - $p_{old}$),将这 10,000 个值存储在 **p_diffs** 中。test = sum(np.random.binomial(2, 0.5, 100000) == 2) / 100000
print(test)p_diffs = []for i in range(10000):new_page_converted = np.random.binomial(1, p_new, n_new)old_page_converted = np.random.binomial(1, p_old, n_old)new_page_p = new_page_converted.mean()old_page_p = old_page_converted.mean()p_diffs.append(new_page_p - old_page_p)# 上述工具略微不同。但是结果都非常相似。两种结果的差额都在0 附件,最大差别也就上下浮动0.004左右。# j. **p_diffs**列表的数值中,有多少比例的数值会大于 **ab_data.csv** 中观察到的实际**转化率差异** ?actual_diff = (df2[df2['group'] == "treatment"]['converted'].mean()) - (df2[df2['group'] == "control"]['converted'].mean())
actual_diffp_diffs = np.array(p_diffs)
(p_diffs > actual_diff).mean()# k. 用文字解释一下你刚才在 **j.** 中计算出来的结果。在数据研究中,这个值是什么? 根据这个数值,请判断新旧页面的转化率是否有显著差异。
#
# **在这里给出你的答案。**# actual_diff 实际差异 表示根据我们的数据,新页和旧页的转换率之间的差异。# p-diffs表示基于10000个模拟样本的新页面和旧页面的转换率之间的模拟差异。# 90.5的百分比在科学上称为p值,它确定了在原假设为真的情况下获得我们观察到的统计数据的概率。# l. 我们也可以使用一个内置程序 (built-in)来实现类似的结果。使用内置程序可能很容易就能取得结果,但上面的内容仍然很重要,
# 它可以训练你具有正确的数据统计思维。
# 填写下面的内容来计算每个页面的转化次数,以及收到每个页面的用户数。计算新旧页面出现的次数,
# 也就是数据中 `n_old` 与 `n_new` 分别出现的行数。这篇关于abtest的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!