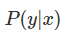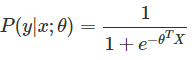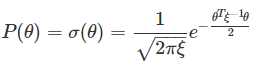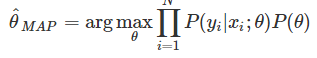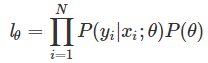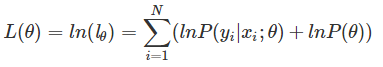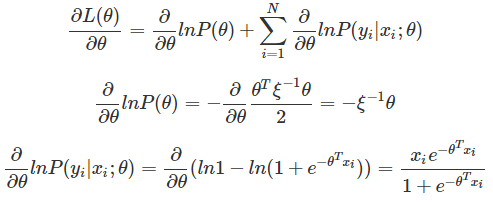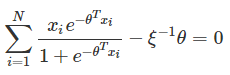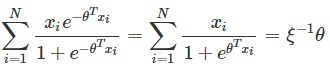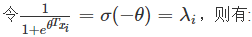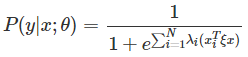本文主要是介绍再谈Fisher Vector,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
原文链接:http://bucktoothsir.github.io/blog/2014/11/24/9-th/
Fisher Vector(1)
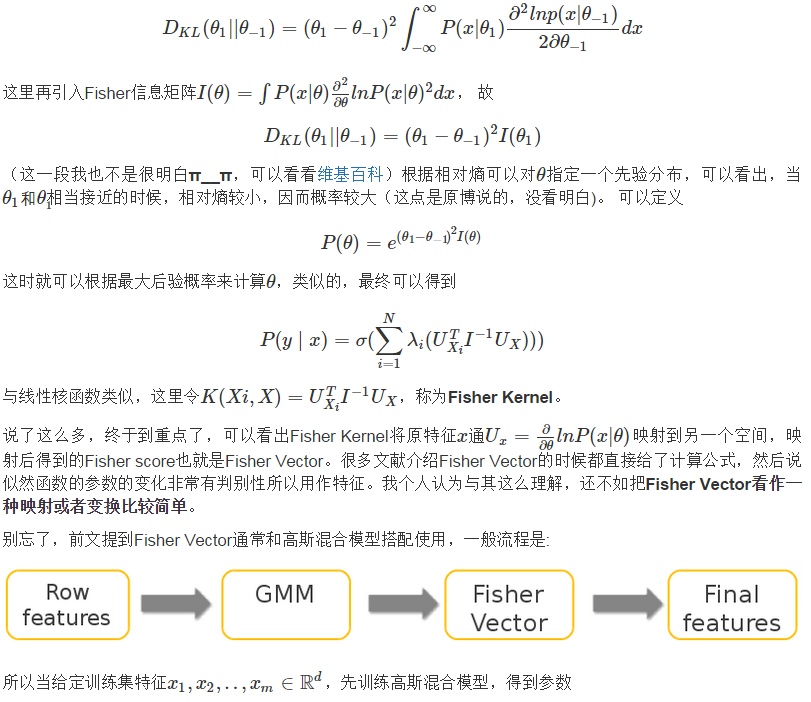
在高斯混合模型中,我提到了特征处理的一般流程:
事实上高斯混合模型完成的是k-means的任务,那么通过高斯混合模型聚类后,也用一般的基于距离的方法进行feature encoding么?不是的,高斯混合模型通常和Fisher Vector一起使用(而Kmeans一般与Bag of Words一起使用,BOW模型一般也是上述流程框图)。现在就来对Fisher Vector做个简单介绍。
Kernel Trick
要理解Fisher Vector, 也要先了解下Kernel。知乎上关于Kernel的问题我比较赞同第三个答案。Kernel不是一种神秘的东西,只是一种计算的trick。 在CV界中亘古不变的主题分类中,假设要训练一个 (−1,1) 的二分类器,则当有一个新样本的时候,则其属于一类 y 的概率为:
可以看出这是一个判别模型,利用logistic function对其建模(为什么使用logistic function可以参考Andrew Ng的机器学习讲义):
我们的目标是找到最好的θ(θ是向量),如果样本很多的话,可以通过最大似然估计找到一组最佳的θ^来达到最好的分类效果。但是在样本较少的情况下,可假设θ的先验概率分布服从均值0的高斯分布,即θ~N(0,ξ),ξ可通过统计样本得到,那么有
利用最大后验概率来估计,假设一共有N个样本xi(i=1,2,3,…,N),且相互独立,则
对lθ两边取ln对数,则:
对θ求导:
令 ∂L(θ)∂θ=0 ,有
求解过程如下:
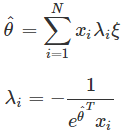
将结果带入 P(y|x;θ),最终得到:
令K(xi,x)=xTiξx为核函数,该核函数为线性核。
Fisher Vector(2)



这篇关于再谈Fisher Vector的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!