34. 二叉树中和为某一值的路径

本文主要是介绍34. 二叉树中和为某一值的路径，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

---

comments: true
difficulty: 中等
edit_url: https://github.com/doocs/leetcode/edit/main/lcof/%E9%9D%A2%E8%AF%95%E9%A2%9834.%20%E4%BA%8C%E5%8F%89%E6%A0%91%E4%B8%AD%E5%92%8C%E4%B8%BA%E6%9F%90%E4%B8%80%E5%80%BC%E7%9A%84%E8%B7%AF%E5%BE%84/README.md

面试题 34. 二叉树中和为某一值的路径

题目描述

给你二叉树的根节点 root 和一个整数目标和 targetSum ，找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。

叶子节点 是指没有子节点的节点。

 

示例 1：

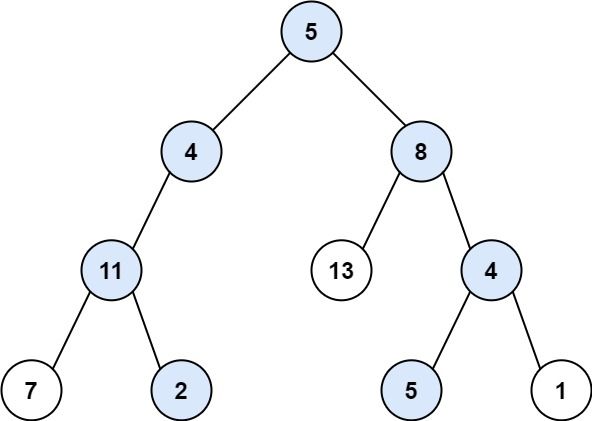
输入：root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出：[[5,4,11,2],[5,8,4,5]]

示例 2：

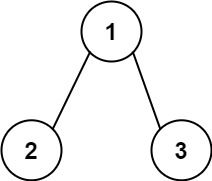
输入：root = [1,2,3], targetSum = 5
输出：[]

示例 3：

输入：root = [1,2], targetSum = 0
输出：[]

 

提示：

• 树中节点总数在范围 [0, 5000] 内
• -1000 <= Node.val <= 1000
• -1000 <= targetSum <= 1000

注意：本题与主站 113 题相同：https://leetcode.cn/problems/path-sum-ii/

解法

方法一：递归

从根节点开始，递归遍历每个节点，每次递归时，将当前节点值加入到路径中，然后判断当前节点是否为叶子节点，如果是叶子节点并且路径和等于目标值，则将该路径加入到结果中。如果当前节点不是叶子节点，则递归遍历其左右子节点。递归遍历时，需要将当前节点从路径中移除，以确保返回父节点时路径刚好是从根节点到父节点。

时间复杂度 $O(n^2)$，空间复杂度 $O(n)$。其中 $n$ 是二叉树的节点数。

Python3

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:def pathSum(self, root: TreeNode, target: int) -> List[List[int]]:def dfs(root, s):if root is None:return#加入节点的同时，检查路径是否满足t.append(root.val)s -= root.valif root.left is None and root.right is None and s == 0:#root不能为空ans.append(t[:]) #t会动态改变dfs(root.left, s)dfs(root.right, s)t.pop() #这种写法，回溯时不需要s+=root.valans = []t = []dfs(root, target)return ans

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = Noneclass Solution(object):def findPath(self, root, sum):""":type root: TreeNode:type sum: int:rtype: List[List[int]]"""def dfs(root):nonlocal sif root is None:returnt.append(root.val)s-=root.valif root.left is None and root.right is None and s==0:ans.append(t[:])dfs(root.left)dfs(root.right)t.pop()s+=root.valans = []t=[]s=sumdfs(root)return ans

Java

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {private List<Integer> t = new ArrayList<>();private List<List<Integer>> ans = new ArrayList<>();public List<List<Integer>> pathSum(TreeNode root, int target) {dfs(root, target);return ans;}private void dfs(TreeNode root, int s) {if (root == null) {return;}t.add(root.val);s -= root.val;if (root.left == null && root.right == null && s == 0) {ans.add(new ArrayList<>(t));}dfs(root.left, s);dfs(root.right, s);t.remove(t.size() - 1);}
}

C++

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<vector<int>> pathSum(TreeNode* root, int target) {vector<vector<int>> ans;vector<int> t;function<void(TreeNode * root, int s)> dfs = [&](TreeNode* root, int s) {if (!root) {return;}t.push_back(root->val);s -= root->val;if (!root->left && !root->right && !s) {ans.push_back(t);}dfs(root->left, s);dfs(root->right, s);t.pop_back();};dfs(root, target);return ans;}
};

Go

/*** Definition for a binary tree node.* type TreeNode struct {*     Val int*     Left *TreeNode*     Right *TreeNode* }*/
func pathSum(root *TreeNode, target int) (ans [][]int) {t := []int{}var dfs func(*TreeNode, int)dfs = func(root *TreeNode, s int) {if root == nil {return}t = append(t, root.Val)s -= root.Valif root.Left == nil && root.Right == nil && s == 0 {ans = append(ans, slices.Clone(t))}dfs(root.Left, s)dfs(root.Right, s)t = t[:len(t)-1]}dfs(root, target)return
}

TypeScript

/*** Definition for a binary tree node.* class TreeNode {*     val: number*     left: TreeNode | null*     right: TreeNode | null*     constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {*         this.val = (val===undefined ? 0 : val)*         this.left = (left===undefined ? null : left)*         this.right = (right===undefined ? null : right)*     }* }*/function pathSum(root: TreeNode | null, target: number): number[][] {const ans: number[][] = [];const t: number[] = [];const dfs = (root: TreeNode | null, s: number): void => {if (!root) {return;}const { val, left, right } = root;t.push(val);s -= val;if (!left && !right && s === 0) {ans.push([...t]);}dfs(left, s);dfs(right, s);t.pop();};dfs(root, target);return ans;
}

Rust

// Definition for a binary tree node.
// #[derive(Debug, PartialEq, Eq)]
// pub struct TreeNode {
//   pub val: i32,
//   pub left: Option<Rc<RefCell<TreeNode>>>,
//   pub right: Option<Rc<RefCell<TreeNode>>>,
// }
//
// impl TreeNode {
//   #[inline]
//   pub fn new(val: i32) -> Self {
//     TreeNode {
//       val,
//       left: None,
//       right: None
//     }
//   }
// }
use std::cell::RefCell;
use std::rc::Rc;
impl Solution {fn dfs(root: &Option<Rc<RefCell<TreeNode>>>,mut target: i32,t: &mut Vec<i32>,ans: &mut Vec<Vec<i32>>,) {if let Some(node) = root.as_ref() {let node = node.borrow();t.push(node.val);target -= node.val;if node.left.is_none() && node.right.is_none() && target == 0 {ans.push(t.clone());}Self::dfs(&node.left, target, t, ans);Self::dfs(&node.right, target, t, ans);t.pop();}}pub fn path_sum(root: Option<Rc<RefCell<TreeNode>>>, target: i32) -> Vec<Vec<i32>> {let mut ans = vec![];Self::dfs(&root, target, &mut vec![], &mut ans);ans}
}

JavaScript

/*** Definition for a binary tree node.* function TreeNode(val, left, right) {*     this.val = (val===undefined ? 0 : val)*     this.left = (left===undefined ? null : left)*     this.right = (right===undefined ? null : right)* }*/
/*** @param {TreeNode} root* @param {number} target* @return {number[][]}*/
var pathSum = function (root, target) {const ans = [];const t = [];const dfs = (root, s) => {if (!root) {return;}const { val, left, right } = root;t.push(val);s -= val;if (!left && !right && !s) {ans.push([...t]);}dfs(left, s);dfs(right, s);t.pop();};dfs(root, target);return ans;
};

C#

/*** Definition for a binary tree node.* public class TreeNode {*     public int val;*     public TreeNode left;*     public TreeNode right;*     public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
public class Solution {private List<IList<int>> ans = new List<IList<int>>();private List<int> t = new List<int>();public IList<IList<int>> PathSum(TreeNode root, int target) {dfs(root, target);return ans;}private void dfs(TreeNode root, int s) {if (root == null) {return;}t.Add(root.val);s -= root.val;if (root.left == null && root.right == null && s == 0) {ans.Add(new List<int>(t));}dfs(root.left, s);dfs(root.right, s);t.RemoveAt(t.Count - 1);}
}

Swift

/*** Definition for a binary tree node.* public class TreeNode {*     public var val: Int*     public var left: TreeNode?*     public var right: TreeNode?*     public init() { self.val = 0; self.left = nil; self.right = nil; }*     public init(_ val: Int) { self.val = val; self.left = nil; self.right = nil; }*     public init(_ val: Int, _ left: TreeNode?, _ right: TreeNode?) {*         self.val = val*         self.left = left*         self.right = right*     }* }*/class Solution {private var t = [Int]()private var ans = [[Int]]()func pathSum(_ root: TreeNode?, _ target: Int) -> [[Int]] {dfs(root, target)return ans}private func dfs(_ root: TreeNode?, _ s: Int) {guard let root = root else {return}t.append(root.val)let remainingSum = s - root.valif root.left == nil && root.right == nil && remainingSum == 0 {ans.append(Array(t))}dfs(root.left, remainingSum)dfs(root.right, remainingSum)t.removeLast()}
}

这篇关于34. 二叉树中和为某一值的路径的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---