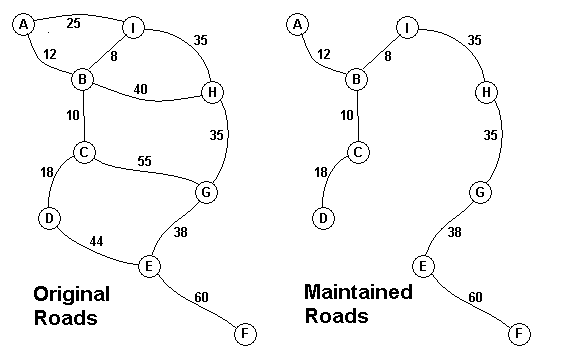
NYOJ 434 POJ 1251 Jungle Roads(最小生成树)

本文主要是介绍NYOJ 434 POJ 1251 Jungle Roads(最小生成树)，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

链接：click here

题意：

题目大意在相通n个岛屿的所有桥都坏了，要重修，重修每一个桥所用的时间不同，求重修使每个岛屿都间接或直接与其他岛屿相同时所用的的最短时间（只有修完一个桥后才可修下一个桥）。简言之就是求最小生成树。

对于数据，数据输入的第一行n代表岛屿的个数，当为0是结束程序，接着n-1行开始时为这岛屿的编号，用大写字母表示，接着是一个整数m，表示与该岛屿连接的字典序大于该岛屿编号的个数，然后该行输入m对数据，每对数据的第一个字母表示与该岛屿连通的岛屿的编号，第二个数字表示要重修两岛屿之间桥所需要的时间，输出数据见样例及原题。

代码：（prim）

 
#include <math.h>
#include <queue>
#include <deque>
#include <vector>
#include <stack>
#include <stdio.h>
#include <ctype.h>
#include <string.h>
#include <stdlib.h>
#include <iostream>
#include <algorithm>using namespace std;
#define Max(a,b) a>b?a:b
#define Min(a,b) a>b?b:a
#define mem(a,b) memset(a,b,sizeof(a))
int dir[4][2]= {{1,0},{-1,0},{0,1},{0,-1}};
const double eps = 1e-6;
const double Pi = acos(-1.0);
static const int inf= ~0U>>2;
static const int maxn = 502;
int mapp[30][30];
int prim(int n)
{int visit[30]= {0};int dis[30];int sum,i,j,k,min;sum=0;for(i=0; i<n; ++i)dis[i]=mapp[0][i];visit[0]=1;for(i=1; i<n; ++i){min=inf;k=0;for(j=0; j<n; ++j){if(!visit[j]&&min>dis[j]){min=dis[j];k=j;}}visit[k]=1;if(min!=inf)sum+=min;for(j=0; j<n; ++j){if(!visit[j]&&dis[j]>mapp[k][j])dis[j]=mapp[k][j];}}return sum;
}
int main()
{int n,len,k,i,j;char str[5],st[5];while(scanf("%d",&n),n){for(i=0; i<n; ++i)for(j=0; j<i; ++j)mapp[i][j]=mapp[j][i]=inf;for(i=1; i<n; ++i){scanf("%s%d",str,&k);while(k--){scanf("%s%d",st,&len);mapp[str[0]-'A'][st[0]-'A']=mapp[st[0]-'A'][str[0]-'A']=len;}}int ans=prim(n);printf("%d\n",ans);}return 0;
}

当然此题稀疏图更好用Kruskal算法实现，在次不写了，网络代码：

/*
Kruskal算法的基本思想
假设WN=(V,{E})是一个含有n个顶点的连通网，则按照克鲁斯卡尔算法构造最小生成树的过程为：
先构造一个只含n个顶点，而边集为空的子图，
若将该子图中各个顶点看成是各棵树上的根结点，则它是一个含有n棵树的一个森林。
之后，从网的边集E中选取一条权值最小的边，若该条边的两个顶点分属不同的树，则将其加入子图，
也就是说，将这两个顶点分别所在的两棵树合成一棵树；
反之，若该条边的两个顶点已落在同一棵树上，则不可取，而应该取下一条权值最小的边再试之。
依次类推，直至森林中只有一棵树，也即子图中含有n-1条边为止。
*/
#include<iostream>
#include<cstdlib>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
using namespace std;
const int inf = ( 1 << 20 ) ;
int p[27];        //    并查集，用于判断两点是否直接或间接连通
struct prog {int u;int v;int w;
}map[80];//存储边的信息，包括起点/终点/权值
bool cmp ( prog a , prog b)
{//排序函数，将边根据权值从小到大排return a.w<b.w;
}
int find(int x)
{//并查集的find，不解释return x==p[x]?x:p[x]=find(p[x]);
}
int main()
{int n;while ( cin >> n , n ) {int i , j ;for  ( i = 0 ; i < 27  ; i ++ )p[i] = i ;//并查集初始化int k = 0 ;for ( i = 0 ; i < n - 1 ; i ++ ){//构造边的信息char str[3];int m;cin >> str >> m ;for ( j = 0 ; j < m ; j ++ ,k ++ ){char str2[3];int t;cin >> str2 >> t ;map[k].u=(str[0]-'A');map[k].v=(str2[0]-'A');map[k].w=t;}}sort ( map , map + k , cmp );//将边从小到大排序int ans=0;        //所要求的答案for ( i = 0 ; i < k ; i ++ ){int x = find(map[i].u);int y = find(map[i].v);if( x!=y){//如果两点不在同一连通分量里，则将两点连接，并存储该边ans+=map[i].w;p[x]=y;}}cout<<ans<<endl;}return 0;
}