本文主要是介绍HDU | Labyrinth,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
Labyrinth
参考博客:http://blog.csdn.net/lttree/article/details/26590299
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=4826
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K
(Java/Others) Total Submission(s): 855 Accepted Submission(s): 388Problem Description
度度熊是一只喜欢探险的熊,一次偶然落进了一个m*n矩阵的迷宫,该迷宫只能从矩阵左上角第一个方格开始走,只有走到右上角的第一个格子才算走出迷宫,每一次只能走一格,且只能向上向下向右走以前没有走过的格子,每一个格子中都有一些金币(或正或负,有可能遇到强盗拦路抢劫,度度熊身上金币可以为负,需要给强盗写欠条),度度熊刚开始时身上金币数为0,问度度熊走出迷宫时候身上最多有多少金币?Input
输入的第一行是一个整数T(T < 200),表示共有T组数据。
每组数据的第一行输入两个正整数m,n(m<=100,n<=100)。接下来的m行,每行n个整数,分别代表相应格子中能得到金币的数量,每个整数都大于等于-100且小于等于100。Output
对于每组数据,首先需要输出单独一行”Case #?:”,其中问号处应填入当前的数据组数,组数从1开始计算。
每组测试数据输出一行,输出一个整数,代表根据最优的打法,你走到右上角时可以获得的最大金币数目。Sample Input
2
3 4
1 -1 1 0
2 -2 4 2
3 5 1 -90
2 2
1 1
1 1Sample Output
Case #1:
18
Case #2:
4Source 2014年百度之星程序设计大赛 - 资格赛
写这道题的时候是在LeetCode上看到的,被分类在了线性DP一栏,刚学DP,所以做一些简单的总结。
这道题咋一看是走迷宫的题目~~ 事实上我也是这么想的…..
不过被放在线性DP这里,才发现用搜索会超时的~
这里仔细列出整个动归的过程。
首先我们可以知道,一个格子是有可能从左边、上边、右边三个方向到达的。
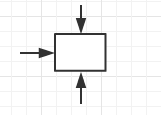
而我们需要从左上角走到右上角,进行阶段划分,我们将每一列作为一个阶段。每一列的每一行对应一个状态。
于是,第0行我们将获取到m个状态。也就是从左上角分别走到对应位置能获得的金币数量,这比较简单,一定是从最上面累加下来。于是dp[i][0]可求。
考虑dp[i][j]的情况,dp[i][j]有可能从三个方向求得,如下图
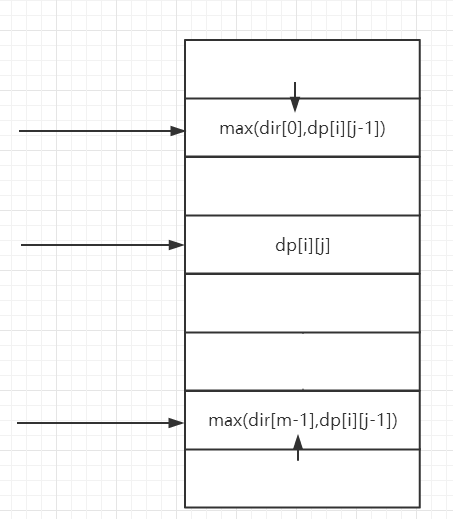
可以设置两个数组dir1和dir2,分别从最上面和最下面开始往下/上 扫描。
对于每一点的最大值,可以由max(dir[i-1],dp[i][j-1])+dp[i][j]决定。
也就是只考虑从左边和上边过来的情况。这样将问题缩减到2个方向。
所以必然是取左边或者上边已经取到的最大值,+这一点的金币数量。
从下往上的情况也相同。
于是可以得出从上或者从下过来的每一点的最大值。
再对整列进行扫描,可以得到当前列可能获取到的最大值。
于是,最终结果是dp[0][n-1],到达右上角
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#define N 101int map[N][N];
int dir1[N],dir2[N];int max(int a,int b){return a>b?a:b;
}int main(){int t,n,m,count=0;scanf("%d",&t);while(t--){scanf("%d%d",&m,&n);memset(map,0,sizeof(map));memset(dir1,0,sizeof(dir1));memset(dir2,0,sizeof(dir2));for(int i=0;i<m;i++){for(int j=0;j<n;j++){scanf("%d",&map[i][j]);}}//预处理第一行for(int i=1;i<m;i++)map[i][0]+=map[i-1][0];//从第二行开始for(int j=1;j<n;j++){//计算由上而下的最大值dir1[0]=map[0][j-1]+map[0][j];for(int i=1;i<m;i++) dir1[i]=max(dir1[i-1],map[i][j-1])+map[i][j];//计算由下而上的最大值dir2[m-1]=map[m-1][j-1]+map[m-1][j];for(int i=m-2;i>=0;i--)dir2[i]=max(dir2[i+1],map[i][j-1])+map[i][j];//计算这些点的最大值for(int i=0;i<m;i++) {map[i][j]=max(dir1[i],dir2[i]);}}printf("Case #%d:\n%d\n",++count,map[0][n-1]);}}这篇关于HDU | Labyrinth的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



