热题系列章节6

本文主要是介绍热题系列章节6，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

297. 二叉树的序列化与反序列化

序列化是将一个数据结构或者对象转换为连续的比特位的操作，进而可以将转换后的数据存储在一个文件或者内存中，同时也可以通过网络传输到另一个计算机环境，采取相反方式重构得到原数据。

请设计一个算法来实现二叉树的序列化与反序列化。这里不限定你的序列 / 反序列化算法执行逻辑，你只需要保证一个二叉树可以被序列化为一个字符串并且将这个字符串反序列化为原始的树结构。

示例:

你可以将以下二叉树：

    1/ \2   3/ \4   5序列化为 "[1,2,3,null,null,4,5]"

示: 这与 LeetCode 目前使用的方式一致，详情请参阅 LeetCode 序列化二叉树的格式。你并非必须采取这种方式，你也可以采用其他的方法解决这个问题。

说明: 不要使用类的成员 / 全局 / 静态变量来存储状态，你的序列化和反序列化算法应该是无状态的。

解题思路
思路：深度优先搜索

根据题目，我们可以了解到。其实二叉树序列化，是将二叉树按照某种遍历方式以某种格式保存为字符串。在本篇幅当中，我们使用的方法是使用深度优先搜索来达到这个目的。

在这里，我们使用的深度优先搜索的思路，用递归实现，在此过程中，我们使用先序遍历的方式来进行解决。

我们使用递归的时候，只需要关注单个节点，剩下就交给递归实现。使用先序遍历的是因为：先序遍历的访问顺序是先访问根节点，然后遍历左子树，最后遍历右子树。这样在我们首先反序列化的时候能够直接定位到根节点。

这里有个需要注意的地方，当遇到 null 节点的时候，要进行标识。这样在反序列化的时候才能够分辨出这里是 null 节点。

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = Noneclass Codec:def serialize(self, root):"""Encodes a tree to a single string.:type root: TreeNode:rtype: str"""if root == None:return 'null,'left_serialize = self.serialize(root.left)right_serialize = self.serialize(root.right)return str(root.val) + ',' + left_serialize + right_serializedef deserialize(self, data):"""Decodes your encoded data to tree.:type data: str:rtype: TreeNode"""def dfs(queue):val = queue.popleft()if val == 'null':return Nonenode =  TreeNode(val)node.left = dfs(queue)node.right = dfs(queue)return nodefrom collections import dequequeue = deque(data.split(','))return dfs(queue)# Your Codec object will be instantiated and called as such:
# codec = Codec()
# codec.deserialize(codec.serialize(root))

224. 基本计算器

给你一个字符串表达式 s ，请你实现一个基本计算器来计算并返回它的值。

注意:不允许使用任何将字符串作为数学表达式计算的内置函数，比如 eval() 。

示例 1：
输入：s = “1 + 1”
输出：2

示例 2：
输入：s = " 2-1 + 2 "
输出：3

示例 3：
输入：s = “(1+(4+5+2)-3)+(6+8)”
输出：23

解题方法
栈
这个题没有乘除法，也就少了计算优先级的判断了。众所周知，实现计算器需要使用一个栈，来保存之前的结果，把后面的结果计算出来之后，和栈里的数字进行操作。

使用了res表示不包括栈里数字在内的结果，num表示当前操作的数字，sign表示运算符的正负，用栈保存遇到括号时前面计算好了的结果和运算符。

操作的步骤是：

如果当前是数字，那么更新计算当前数字；
如果当前是操作符+或者-，那么需要更新计算当前计算的结果res，并把当前数字num设为0，sign设为正负，重新开始；
如果当前是(，那么说明后面的小括号里的内容需要优先计算，所以要把res，sign进栈，更新res和sign为新的开始；
如果当前是)，那么说明当前括号里的内容已经计算完毕，所以要把之前的结果出栈，然后计算整个式子的结果；
最后，当所有数字结束的时候，需要把结果进行计算，确保结果是正确的。

提示：
1 <= s.length <= 3 * 105
s 由数字、‘+’、‘-’、‘(’、‘)’、和 ’ ’ 组成
s 表示一个有效的表达式
‘+’ 不能用作一元运算(例如， “+1” 和 “+(2 + 3)” 无效)
‘-’ 可以用作一元运算(即 “-1” 和 “-(2 + 3)” 是有效的)
输入中不存在两个连续的操作符
每个数字和运行的计算将适合于一个有符号的 32位 整数

class Solution:def calculate(self, s: str) -> int:""":type s: str:rtype: int"""res, num, sign = 0, 0, 1stack = []for c in s:if c.isdigit():num = 10 * num + int(c)elif c == "+" or c == "-":res = res + sign * numnum = 0sign = 1 if c == "+" else -1elif c == "(":stack.append(res)stack.append(sign)res = 0sign = 1elif c == ")":res = res + sign * numnum = 0res *= stack.pop()res += stack.pop()res = res + sign * numreturn res

460. LFU缓存

题目：请你设计并实现一个满足 LRU (最近最少使用) 缓存 约束的数据结构。实现LRUCache类：

LRUCache(int capacity) 以正整数作为容量capacity初始化 LRU 缓存
int get(int key) 如果关键字key存在于缓存中，则返回关键字的值，否则返回-1 。
void put(int key, int value) 如果关键字key已经存在，则变更其数据值value；如果不存在，则向缓存中插入该组key-value。如果插入操作导致关键字数量超过capacity，则应该 逐出 最久未使用的关键字。
函数get和put必须以O(1)的平均时间复杂度运行。
示例
输入[“LRUCache”, “put”, “put”, “get”, “put”, “get”, “put”, “get”, “get”, “get”][[2], [1, 1], [2, 2], [1], [3, 3], [2], [4, 4], [1], [3], [4]]
输出[null, null, null, 1, null, -1, null, -1, 3, 4]
解释LRUCache lRUCache = new LRUCache(2);lRUCache.put(1, 1); // 缓存是 {1=1}lRUCache.put(2, 2); // 缓存是 {1=1, 2=2}lRUCache.get(1); // 返回 1lRUCache.put(3, 3); // 该操作会使得关键字 2 作废，缓存是 {1=1, 3=3}lRUCache.get(2); // 返回 -1 (未找到)lRUCache.put(4, 4); // 该操作会使得关键字 1 作废，缓存是 {4=4, 3=3}lRUCache.get(1); // 返回 -1 (未找到)lRUCache.get(3); // 返回 3lRUCache.get(4); // 返回 4

LRUCache cache = new LRUCache( 2 /* capacity */ );cache.put(1, 1);
cache.put(2, 2);
cache.get(1);       // returns 1
cache.put(3, 3);    // evicts key 2
cache.get(2);       // returns -1 (not found)
cache.put(4, 4);    // evicts key 1
cache.get(1);       // returns -1 (not found)
cache.get(3);       // returns 3
cache.get(4);       // returns 4

标题题解
该题目的核心主要是get与put函数。get函数的要求非常简单就是通过key获取相应的value，hash表即可满足题目要求。put函数主要超过capacity的时候需要把最久未使用的关键字删除，再添加新的key-value。这里显然需要对key进行排序，自然想到的就是Python3中collections中的OrderedDict。代码如下：

class LRUCache:def __init__(self, capacity: int):#定义一个dictself.capacity=capacity#定义一个有序字典self.LRU_dic=collections.OrderedDict()#使用一个变量记录dic的数据量self.used_num=0def get(self, key: int) -> int:if key in self.LRU_dic:#如果被使用了利用move_to_end移动到队尾，保证了LRU_dic是按使用顺序排序的self.LRU_dic.move_to_end(key)return self.LRU_dic.get(key)else:return -1def put(self, key: int, value: int) -> None:if key in self.LRU_dic:         self.LRU_dic[key]=valueself.LRU_dic.move_to_end(key)else:#判断当前已有数量是否超过capacityif self.used_num==self.capacity:#删除首个key，因为首个key是最久未使用的self.LRU_dic.popitem(last=False)self.used_num-=1self.LRU_dic[key]=valueself.used_num+=1

然后，直接调用包通常不是面试的时候考察的主要能力。因此需要根据一些数据结构来实现OrderedDict类似的功能。
可以发现哈希表肯定是需要的，能存储key,value相关信息。这里一个主要的需求是一个序的数据结构能在头部与尾部都实现O(1)时间复杂度的操作。list也能满足这个要求，但是list对于元素的查询、更新以及有排序操作的支持不是很友好。显然这里使用双向链表比较合适。下面详细介绍一下哈希表与双向链表。数据结构清楚了实现就比较容易了。
先介绍下双向链表。

pre表示前向指针，key,value就是键值，next表示下一步指针指的节点。初始化只有head与tail两个节点，这里把新使用的节点放到链表尾部，头部链表节点就是最久未使用的节点。

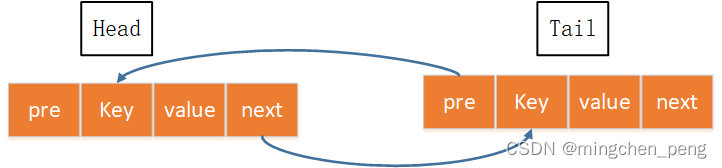
因为使用过的key需要把相应的链表节点移动到队尾，因此需要实现类似OrderedDict的move_to_end这个函数的功能。如果超出capacity的时候要删除最久未使用的节点也就是删除head.next节点，也需要实现一个表头节点删除的功能。定义完链表，hash表就好实现了key，对应给定的key，value对应的是双向链表中的节点。这样通过key就能在O(1)时间定位到双向链表中的节点。代码实现如下：

class LRUCache:class D_link:def __init__(self,key=0,value=0):self.key=keyself.value=valueself.pre=Noneself.next=Nonedef __init__(self, capacity: int):#定义一个dictself.capacity=capacityself.LRU_dic={}#使用一个变量记录dic的数据量self.used_num=0#初始化双向链表self.head=LRUCache.D_link()self.tail=LRUCache.D_link()self.head.next=self.tailself.tail.pre=self.headdef get(self, key: int) -> int:if key in self.LRU_dic:node=self.LRU_dic.get(key)#因为访问过需要移动到链表尾self.move_to_end(node)return node.valueelse:return -1def put(self, key: int, value: int) -> None:if key in self.LRU_dic:#更新LRU_dic的value         node= self.LRU_dic[key]node.value=valueself.move_to_end(node)else:#判断当前已有数量是否超过capacityif self.used_num==self.capacity:#删除双链表最前面的Nodedel_key=self.del_head()self.used_num-=1#从LRU_dic中删除Keydel self.LRU_dic[del_key]new_node=LRUCache.D_link(key,value)#在链表尾部插入self.insert_node(new_node)self.LRU_dic[key]=new_nodeself.used_num+=1def move_to_end(self,node):#首先把node取出来pre_node=node.prepost_node=node.nextpre_node.next=post_nodepost_node.pre=pre_nodetail_pre=self.tail.pretail_pre.next=nodenode.pre=tail_prenode.next=self.tailself.tail.pre=nodedef del_head(self):key=self.head.next.keypost_node=self.head.next.nextself.head.next=post_nodepost_node.pre=self.headreturn keydef insert_node(self,node):pre_tail=self.tail.prepre_tail.next=nodenode.pre=pre_tailnode.next=self.tailself.tail.pre=node

计算复杂度
时间复杂度,题目要求就是O(1)，这里也是O(1)
空间复杂度，因为链表长度要求是在capacity下的，因此空间复杂度为O(capacity)

==========================================================================

这道题蕴含了LRU缓存算法的实现原理，该算法被广泛应用于资源信息如图片的缓存，提供了一种灵活的缓存策略。在理解这道题之前，需要了解HashMap的原理。HashMap提供了key-value的存储方式，并提供了put和get方法来进行数据存取。但是HashMap是无序的，而现实中我们希望有顺序地去存储key-value时，就需要使用LinkedHashMap了，其中LinkedHashMap的实现也就是利用了双向链表+哈希表。Python的collection模块有一个双向队列deque可以辅助我们较轻松地完成此题，但为了学习，我们打算手写一遍一些算法的实现，以理清细节。

算法思路：

创建一个Node类，用于保存键、值以及前后指针的属性

class Node:def __init__(self, key, val):self.key = keyself.val = valself.pre = Noneself.nxt = None

创建一个DList类，其中具备头节点和尾节点，并拥有添加节点和删除节点两个方法。

class DLinked:def __init__(self, head=None, tail=None):self.head = headself.tail = tail# 双向链表添加节点的方法def add(self, node):passdef remove(self, node):pass

get(key)：如果key存在于保存信息的哈希表hashTable中，则将其在链表中移除并重新加入到表头，并同时返回该值；其中表头的元素代表着最新的元素；反之，如果key不存在，则直接返回-1.

def get(key):# 先取出节点# 如果不存在 则返回Nonenode = self.hashTable.get(key, None)if node:# 双向链表实例val = node.valself.dlinked.remove(node)# 并添加到表头self.dlinked.add(node)return valreturn -1

put(key, value)：如果key存在于保存信息的哈希表中，同样地将相应的节点移除并重新添加到表头，同时更新value值；如果不存在且达到了缓存的最大容量capacity，则将最近最少使用的元素，也就是表尾的元素删除，并也将其从hashTable中删除，将当前key, value分别加入到dlinked以及hashTable中；如果不存在且未达到最大容量，则直接加入即可。

def put(key, value):node = self.hashTable.get(key, None)# 如果存在if node:self.dlinked.remove(node)node.val = valueself.dlinked.add(node)return# 如果不存在且达到了最大容量if self.capacity == len(self.hashTable):# 获取节点tailNode = self.dlinked.tail# 删除# 删除节点方法返回一个 keyoldKey = self.dlinked.remove(tailNode)del self.hashTable[oldKey]# 加入节点# 加入方法返回新加这个节点node = self.dlinked.add(Node(key, value))self.hashTable[key] = node# 否则 直接加入else:node = self.dlinked.add(Node(key, value))self.hashTable[key] = nodereturn		

剩下的工作就是完善双向链表的add与remove方法。

首先是add方法，如果链表没有表头，则直接将节点设为头部，否则加入表头：

def add(self, node):# 如果双向链表没有头节点if self.head == None:self.head = node# 同时如果没有尾节点if self.tail == None:self.tail = nodeelse:# 将节点加入表头self.head.pre = nodenode.nxt = self.headnode.pre = Noneself.head = nodereturn self.head

remove方法稍微复杂一些，需要根据删除的节点在原双向链表的位置进行判断，分别是表头、表中间和表尾处：

def remove(self, node):# 首先获取要删除节点的前后指针pre, nxt = node.pre, node.nxt# 如果只有一个节点if pre is None and nxt is None:self.head = Noneself.tail = Nonereturn node.key# 如果是头节点 且有后续节点if pre is None:nxt.pre = Noneself.head = nxt# 如果是尾节点 且有前续节点elif nxt is None:pre.nxt = Noneself.tail = pre# 中间节点else:pre.nxt = nxtnxt.pre = pre# 返回被删除节点的键return node.key

138. 复制带随机指针的链表

给你一个长度为 n 的链表，每个节点包含一个额外增加的随机指针 random ，该指针可以指向链表中的任何节点或空节点。

构造这个链表的 深拷贝。 深拷贝应该正好由 n 个 全新 节点组成，其中每个新节点的值都设为其对应的原节点的值。新节点的 next 指针和 random 指针也都应指向复制链表中的新节点，并使原链表和复制链表中的这些指针能够表示相同的链表状态。复制链表中的指针都不应指向原链表中的节点 。

例如，如果原链表中有 X 和 Y 两个节点，其中 X.random --> Y 。那么在复制链表中对应的两个节点 x 和 y ，同样有 x.random --> y 。

返回复制链表的头节点。

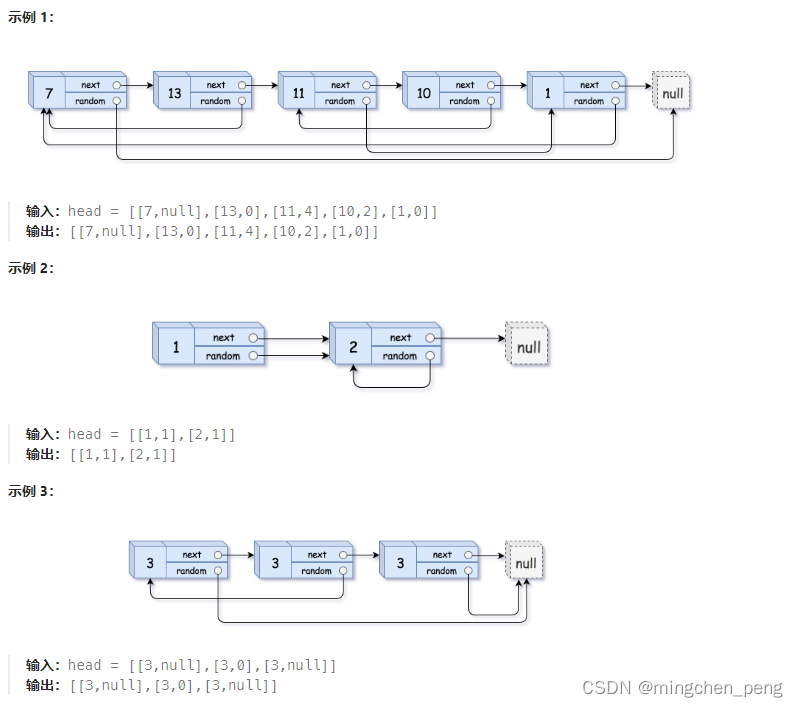
用一个由 n 个节点组成的链表来表示输入/输出中的链表。每个节点用一个 [val, random_index] 表示：

val：一个表示 Node.val 的整数。
random_index：随机指针指向的节点索引（范围从 0 到 n-1）；如果不指向任何节点，则为 null 。
你的代码 只 接受原链表的头节点 head 作为传入参数。

"""
# Definition for a Node.
class Node(object):def __init__(self, val, next, random):self.val = valself.next = nextself.random = random
"""
class Solution(object):def copyRandomList(self, head):""":type head: Node:rtype: Node"""#133变种题， 图换成链表mapping = dict()p = headwhile p:mapping[p] = Node(p.val, None, None)p = p.nextfor key, val in mapping.items(): #key是老结点， val是新节点if key.next:val.next = mapping[key.next]if key.random and key.random in mapping:val.random = mapping[key.random]return mapping[head] if head else head

136. 只出现一次的数字

给你一个 非空 整数数组 nums ，除了某个元素只出现一次以外，其余每个元素均出现两次。找出那个只出现了一次的元素。

你必须设计并实现线性时间复杂度的算法来解决此问题，且该算法只使用常量额外空间。
示例 1 ：
输入：nums = [2,2,1]
输出：1

示例 2 ：
输入：nums = [4,1,2,1,2]
输出：4

示例 3 ：
输入：nums = [1]
输出：1

提示：
1 <= nums.length <= 3 * 104
-3 * 104 <= nums[i] <= 3 * 104
除了某个元素只出现一次以外，其余每个元素均出现两次。

异或计算有以下三个性质
任何数和0做异或计算，结果仍然是原来的数
任何数和其自身做异或计算，结果是0
异或计算满足交换联合结合律，a 异或 b 异或 c = a 异或 （b异或 c）

class Solution:def singleNumber(self, nums: List[int]) -> int:single  = 0for num in nums:single ^= numreturn single

剑指 Offer 36. 二叉搜索树与双向链表

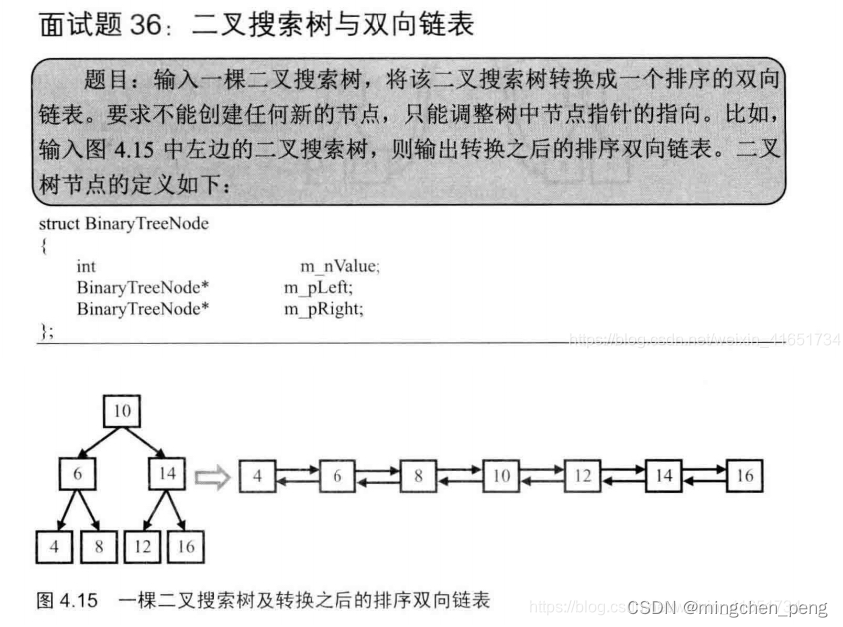
输入一棵二叉搜索树，将该二叉搜索树转换成一个排序的循环双向链表。要求不能创建任何新的节点，只能调整树中节点指针的指向。

为了让您更好地理解问题，以下面的二叉搜索树为例：

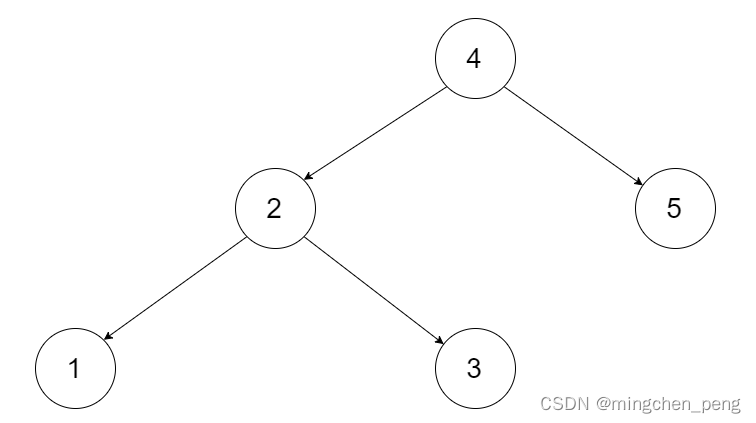
我们希望将这个二叉搜索树转化为双向循环链表。链表中的每个节点都有一个前驱和后继指针。对于双向循环链表，第一个节点的前驱是最后一个节点，最后一个节点的后继是第一个节点。

下图展示了上面的二叉搜索树转化成的链表。“head” 表示指向链表中有最小元素的节点。

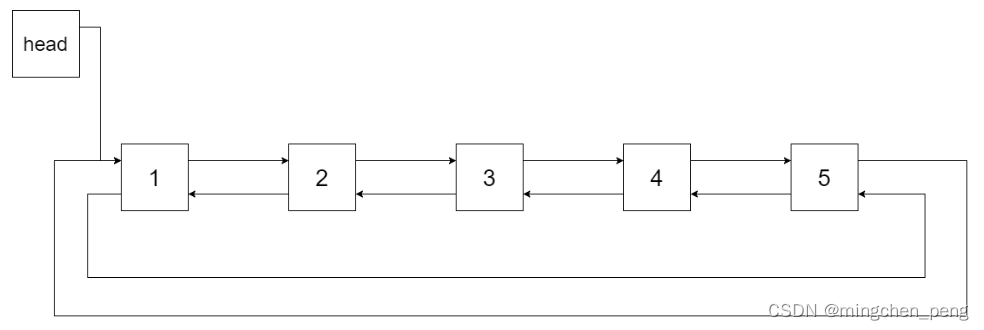
特别地，我们希望可以就地完成转换操作。当转化完成以后，树中节点的左指针需要指向前驱，树中节点的右指针需要指向后继。还需要返回链表中的第一个节点的指针。

"""
# Definition for a Node.
class Node:def __init__(self, val, left=None, right=None):self.val = valself.left = leftself.right = right
"""
class Solution:def treeToDoublyList(self, root: 'Node') -> 'Node':def dfs(cur):if not cur: returndfs(cur.left) # 递归左子树if self.pre: # 修改节点引用self.pre.right, cur.left = cur, self.preelse: # 记录头节点self.head = curself.pre = cur # 保存 curdfs(cur.right) # 递归右子树if not root: returnself.pre = Nonedfs(root)self.head.left, self.pre.right = self.pre, self.headreturn self.head

11. 盛最多水的容器

给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。

找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

返回容器可以储存的最大水量。

说明：你不能倾斜容器。

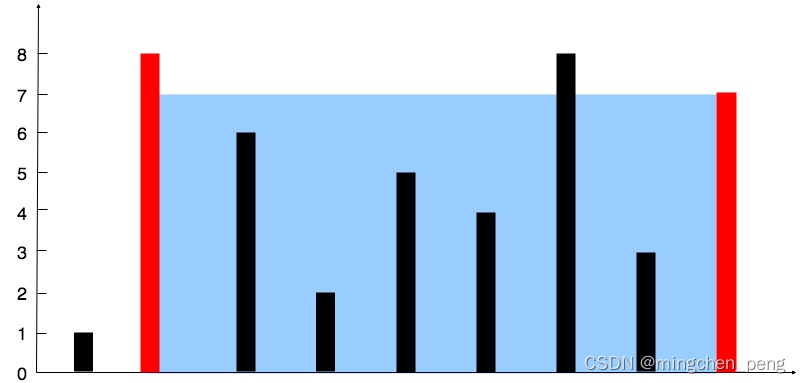
输入：[1,8,6,2,5,4,8,3,7]
输出：49
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

示例 2：
输入：height = [1,1]
输出：1

提示：
n == height.length
2 <= n <= 105
0 <= height[i] <= 104

class Solution:def maxArea(self, height: List[int]) -> int:l,r = 0, len(height) -1res = 0while l < r:if height[l] <= height[r]:res = max(res, height[l]*(r-l))l += 1else:res = max(res, height[r]*(r-l))r -= 1return res

498. 对角线遍历

给定一个含有 M x N 个元素的矩阵（M 行，N 列），请以对角线遍历的顺序返回这个矩阵中的所有元素，对角线遍历如下图所示。

输入:
[[ 1, 2, 3 ],[ 4, 5, 6 ],[ 7, 8, 9 ]
]输出:  [1,2,4,7,5,3,6,8,9]解释:

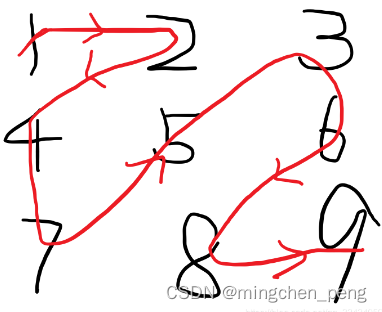
思路：

由观察可以得知，一共有两种走法，向右上方走和向左下方走。（第一个元素也是向右上方走）

再由二维数组的特性可以得知，向右上方走实际上等于 x -= 1, y += 1, 向左下方走实际上等于 x+= 1, y -= 1。

然后再判断什么时候应该转弯：

1. 当向右上方走的时候，有两种情况会造成碰壁，因而需要转弯，

   CASE 1： 碰到上方的壁 （x无法再 - 1），但还没碰到右方的壁（y可以+1）

                 在这种情况下，下一步的坐标为y += 1， 比如上方示例图里的 1 -》 2。
   

   CASE 2： 碰到右方的壁 （y 不能 + 1）

                 在这种情况下，下一步的坐标为x += 1， 比如示例图里的 3 -》 6
   

2. 向左下方走同理：

   CASE1. 碰左壁但未碰下壁：x += 1

   CSSE2. 碰下壁：y += 1

class Solution(object):def findDiagonalOrder(self, matrix):""":type matrix: List[List[int]]:rtype: List[int]"""# 向右上方走，x -= 1, y += 1# 向左下角走，x += 1, y -= 1m = len(matrix)if not m :return []n = len(matrix[0])if not n :return []cnt = 0x, y = 0, 0res = list()direction = "right"while(cnt < m * n):cnt += 1# print direction, x, y, matrix[x][y]res.append(matrix[x][y])if direction == "right":#向右上方走if x >= 1 and y < n - 1: # 不用调换方向x -= 1y += 1continueelse:direction = "left" #调换方向if x == 0 and y < n - 1: #碰上壁y += 1elif  y == n - 1: #碰右壁x += 1else: # 向左下方走if x < m - 1 and y >= 1: # 不用调换方向x += 1y -= 1continueelse:direction = "right" #调换方向if x == m - 1: # 碰下壁y += 1elif y == 0 and x < m - 1: #碰左壁x += 1 # print resreturn res

402. 移掉K位数字

给定一个以字符串表示的非负整数 num，移除这个数中的 k 位数字，使得剩下的数字最小。

注意:
num 的长度小于 10002 且 ≥ k。
num 不会包含任何前导零。

示例 1 :
输入: num = “1432219”, k = 3
输出: “1219”
解释: 移除掉三个数字 4, 3, 和 2 形成一个新的最小的数字 1219。

示例 2 :
输入: num = “10200”, k = 1
输出: “200”
解释: 移掉首位的 1 剩下的数字为 200. 注意输出不能有任何前导零。

示例 3 :
输入: num = “10”, k = 2
输出: “0”
解释: 从原数字移除所有的数字，剩余为空就是0。

解题思路
思路：单调栈
先审题，题目给定一个由字符串表示的非负整数 num，要求移除 k 位数字，使得剩下的数字最小。

其中提及需注意的点如下：

num 不含前导零；
num 的长度小于 10002 且大于等于 k。
那么现在的问题就是，如何确定移除的数字，使得剩余数字最小？

先说下数字比较的问题。当比较非负整数大小时，在不含前导零的情况下，且数字位数相同时，我们需要逐位对比数字的大小，然后确定整体数字的大小。例如：
比较相同位数的 123 和 132
123
132

首位 1 相同，但第二位中 132 的 3 大于 123 中的 2，所以 132 > 123。
也即是说，当两个数字位数相同（两数不等）的情况下，由高位决定大小。
回到本题，现在我们要考虑移除 k 位数字，要想最终得到数字最小，那么我们应该从移除高位较大的数字，保留较小的数字。以示例 1 来进行说明：

输入: num = “1432219”, k = 3
输出: “1219”
解释: 移除掉三个数字 4, 3, 和 2 形成一个新的最小的数字 1219。

这里 k 为 3，需要移除 3 位数字。这里说明下移除 1 位的情况（因为后续的情况思路也是相同的）。

在前面的分析中我们可知，两个数字位数相同（两数不等）的情况，高位决定大小。例子中 “1432219”，我们可以移除任意一个数字，而得到的剩余数字的位数都是相同的。在这里，输出中先将 4 移除，保留剩下的数字，即是优先移除高位较大的数字。

题目中给定的数字是以字符串表示的，那么假设我们将数字用列表的形式表示，现在我们要找高位较大的数字时，做法如下：
从左到右遍历列表，当找到 i （ i > 0 ），使得 n u m [ i − 1 ] > n u m [ i ] ，那么这里我们就可以确定，在这个区间中 n u m [ i − 1 ] 是较大的数字，考虑将其移除。若还需继续移除数字，以同样的做法进行。

这里需要注意，若无法找到 i ii 满足上面的条件时，则表示这个序列是（不严格的）单调递增的，那么可以从序列后面开始移除。

这里不严格的单调递增，表示序列数字可能存在相等的情况。

单调栈
在这里，我们可以考虑使用单调栈的思路来实现上面的策略。

具体的思路如下：
定义栈，从左往右开始遍历字符串；
进行比较，如果遍历的数字小于栈顶的元素，那么进行出栈。
当满足以下条件时，停止出栈：
出栈元素的次数达到 k 次；
栈为空；
栈顶元素不再大于遍历的数字。
若不满足上面的条件时，继续入栈直至遍历结束。
当遍历结束后，这里还需要注意一些问题：

当出栈的数字个数小于 k 时，也即是移除的数字个数不够时，由于此时的栈是单调不减的，那么直接从尾部移除剩下的数字；
如果剩余数字存在前导零的情况时，我们要将前导零删除；
如果最终数字为空时，返回字符串 ‘0’。

class Solution:def removeKdigits(self, num: str, k: int) -> str:# 定义栈stack = []# 开始遍历for digit in num:# 数组 num 的长度一定是大于或等于 k 的# 如果栈顶数字大于遍历数字时，出栈while k > 0 and stack and stack[-1] > digit:stack.pop()k -= 1# 否则入栈stack.append(digit)# 若此时栈为单调递增栈，但是还未移除完 k 位数字# 直接从栈顶移除数字，这里 python 直接用列表切片ans = stack[:-k] if k > 0 else stack# 注意前导 0 的情况return ''.join(ans).lstrip('0') or '0'

79. 单词搜索

给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中，返回 true ；否则，返回 false 。

单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。

示例 1：

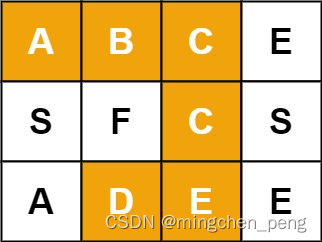
输入：board = [[“A”,“B”,“C”,“E”],[“S”,“F”,“C”,“S”],[“A”,“D”,“E”,“E”]], word = “ABCCED”
输出：true
示例 2：

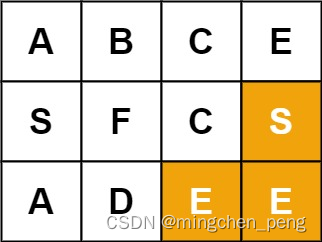
输入：board = [[“A”,“B”,“C”,“E”],[“S”,“F”,“C”,“S”],[“A”,“D”,“E”,“E”]], word = “SEE”
输出：true
示例 3：

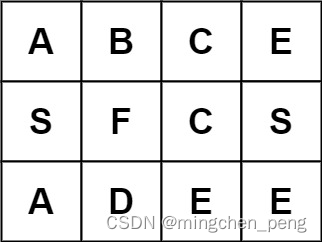
输入：board = [[“A”,“B”,“C”,“E”],[“S”,“F”,“C”,“S”],[“A”,“D”,“E”,“E”]], word = “ABCB”
输出：false

class Solution:def exist(self, board: List[List[str]], word: str) -> bool:m,n = len(board), len(board[0])def dfs(i, j , k):if not 0<=i <m or not 0<=j <n or  board[i][j] != word[k]:return Falseelif k == len(word)-1:return Trueelse:board[i][j] = ''res = dfs(i+1, j , k + 1) or dfs(i-1, j , k+1) or dfs(i, j-1 , k+1) or dfs(i, j+1 , k+1)board[i][j] = word[k]return resfor i in range(m):for j in range(n):if dfs(i, j , 0):return Truereturn False

958. 二叉树的完全性检验

难度中等

给定一个二叉树的 root ，确定它是否是一个 完全二叉树 。

在一个 完全二叉树 中，除了最后一个关卡外，所有关卡都是完全被填满的，并且最后一个关卡中的所有节点都是尽可能靠左的。它可以包含 1 到 2h 节点之间的最后一级 h 。

示例 1：

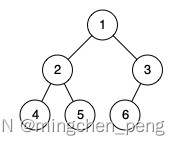
输入：root = [1,2,3,4,5,6]
输出：true
解释：最后一层前的每一层都是满的（即，结点值为 {1} 和 {2,3} 的两层），且最后一层中的所有结点（{4,5,6}）都尽可能地向左。
示例 2：

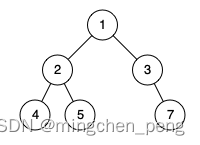
输入：root = [1,2,3,4,5,null,7]
输出：false
解释：值为 7 的结点没有尽可能靠向左侧。
提示：
树的结点数在范围 [1, 100] 内。
1 <= Node.val <= 1000

# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None
#
# 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
#
# 
# @param root TreeNode类 
# @return bool布尔型
#
class Solution:def isCompleteTree(self , root: TreeNode) -> bool:# write code here# 判断完全二叉树：层序遍历，设置flag 判断当前节点是否存在if not root:return node_lst = []node_lst.append(root)flag = Falsewhile node_lst:layer_node = []while node_lst:cur = node_lst.pop(0)if not cur:flag =  Trueelse:if flag:return Falselayer_node.append(cur.left)layer_node.append(cur.right)node_lst.extend(layer_node)return True

这篇关于热题系列章节6的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---