[信号与系统]有关滤波器的一些知识背景

本文主要是介绍[信号与系统]有关滤波器的一些知识背景，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

前言

最近在看FIR和IIR，本文作为前置，需要在理解这两种滤波器之前阅读。

本文内容会详细讲述一下有关滤波器的技术要求。

选频滤波器的频率响应

选频滤波器（Selective Frequency Filter）的频率响应是描述该滤波器在不同频率下对信号的放大或衰减特性的曲线。频率响应是一个复数函数，它包含了幅度响应和相位响应两个方面：

1. 幅度响应（Magnitude Response）：

• 描述滤波器对不同频率信号的增益或衰减。
• 用于确定哪些频率分量通过滤波器时会被放大或减小。

2. 相位响应（Phase Response）：

• 描述滤波器对不同频率信号的相位偏移。
• 重要用于了解信号在经过滤波器后各频率分量的相对时间延迟变化。

频率响应通常用复数形式表示：

$H(f)=A(f)e^{j\theta (f)}$

其中:

• $H(f)$是滤波器在频率f处的响应
• $A(f)$是幅度响应，表示滤波器在频率$f$处的增益
• $\theta (f)$是相位响应，表示滤波器在频率f处引入的相位偏移，即各频率成分通过滤波器后再时间上的延后情况。

幅度响应和相位响应的图示

理想低通滤波器逼近的误差容限

幅度响应

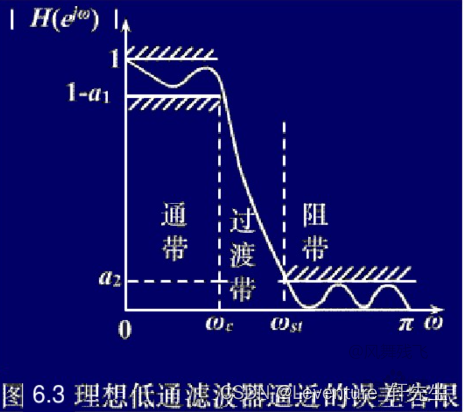
幅度响应图通常表示为频率的函数，以展示滤波器在各个频率点的增益。常见的形式是：

• 通带（Passband）：信号通过滤波器时，频率分量几乎不被衰减的频率范围。
• 阻带（Stopband）：信号通过滤波器时，频率分量被显著衰减的频率范围。
• 过渡带（Transition Band）：从通带到阻带的过渡频率范围。

对于此图：

• $w_c$ : 通带截止频率
• $w_{st}$:阻带截止频率
• ${\alpha }_1$:通带容限
• ${\alpha }_2$:阻带容限

相位响应

相位响应图表示为频率的函数，以展示滤波器在各个频率点的相位偏移。理想的相位响应是线性的，这意味着所有频率分量的相对时间延迟是相同的，信号不会失真。

以下是一个低通滤波器的频率响应示例，它在通带内保持恒定增益，在阻带内快速衰减。

• 幅度响应示例图

|              -----------
|            /|          |
|          /  |          |
|        /    |          |
|      /      |          |
|    /        |          |
|  /          |          |
|/------------|----------
0   f_c      f_s

• 相位响应示例图

|
|
|
|
|\
| \
|  \
|   \
|    \
|     \
|      \
|       \
0        f

在这些图中：

• $f_c$是截止频率cutoff frequency），它是通带和过渡带的分界点。
• $f_s$是采样频率的一半（对于数字滤波器来说），它是奈奎斯特频率。

重要概念

• 通带纹波（Passband Ripple）：在通带内，滤波器增益的变化范围。理想情况下，通带内应保持恒定增益。
• 阻带衰减（Stopband Attenuation）：在阻带内，滤波器对信号衰减的程度。阻带衰减越大，滤波器对不希望通过的频率分量的抑制能力越强。
• 群延迟（Group Delay）：信号各频率分量通过滤波器后的延迟差异。群延迟一致性好意味着滤波器对信号的时间域特性影响小。

关于IIR和FIR的区别中，我们知道FIR滤波器通带的相位延迟比IIR更有优势，因为FIR的相位延迟是线性的，更好优化。

这篇关于[信号与系统]有关滤波器的一些知识背景的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---