树：赫夫曼树赫夫曼编码

2024-06-21 02:38
文章标签 编码 夫曼 树赫

本文主要是介绍树：赫夫曼树赫夫曼编码，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1，赫夫曼树

1.1，赫夫曼树基本介绍及相关概念

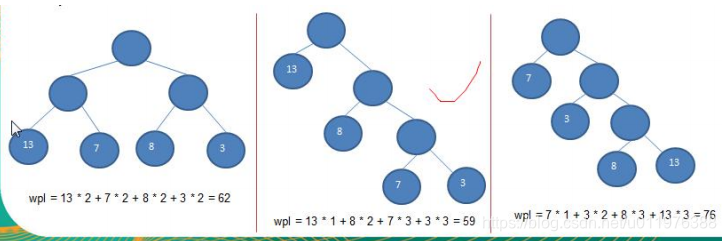
  • 给定n个权值作为n个叶子节点，构造一颗二叉树，若该树的**带权路径长度(WPL)**达到最小，称这样的的二叉树为最优二叉树，也称为赫夫曼树，或者哈夫曼树、霍夫曼树
  • 赫夫曼树是带权路径长度最短的数，权值较大的节点离根较近
  • 路径和路径长度：在一棵树中，从一个节点往下可以达到的孩子和孙子节点之间的通路，称为路径；通路中分支的数量称为路径长度；若规定根节点的层数为1，则从根节点到第L层节点的路径长度为L - 1
  • 节点的权及带权路径长度：若将树中的节点赋给一个有意义的值，则该值称为节点的权；从根节点到该节点的路径长度与该权值的乘积称为该节点的带权路径长度
  • 树的带权路径长度：树的带权路径长度规定为所有叶子节点的带权路径长度之和，记为WPL（Weighted path length），权值越大的节点离根节点越近的二叉树才是最优二叉树，如图：
    在这里插入图片描述

1.2，赫夫曼树基本思想及示意图

  • 首先对要处理的数组从小到大进行排序，每一个数据都可以转换为一个节点，每一个节点都可以看为一个最简单的二叉树（不带左右子节点的二叉树）
  • 从转换好的有序节点集合中，取出两个最小的节点组成一颗二叉树
  • 在这颗新二叉树中，左右子节点分别为取出的两个节点，父节点为这两个子节点的带权路径和
  • 二叉树生成完成后，从节点集合中移除两个最小子节点，并将生成的二叉树父节点加入到集合中
  • 之后再次对集合排序并重复以上操作，直到集合中只有一个元素，这样说明赫夫曼树已经生成完成，可以对该树进行输出查看
  • 对一个数组{13，7，8，3，29，6，1}生成的赫夫曼树如图：
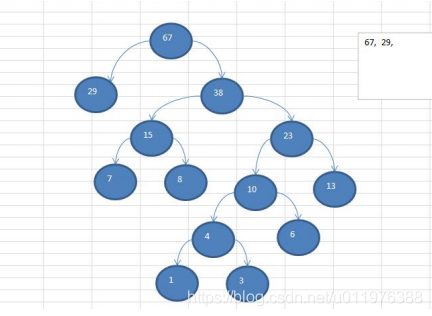
    在这里插入图片描述
  • 先对数组进行排序：{1，3，6，7，8，13，29}
  • 取出前两个元素：{1，3}，生成一个新的二叉树，父节点为两个节点的带权路径和即：data = 1 * 1 + 3 * 1 = 4
  • 将两个节点从数组中移除，并添加父节点到数组中后重新排序，则新的数组元素为：{4，6，7，8，13，29}，其中节点4存在{1，3}两个子节点
  • 以此类推，最终会生成上面的赫夫曼树

1.3，赫夫曼树代码实现

package com.self.datastructure.tree.huffman;import lombok.Data;
import lombok.ToString;import java.util.ArrayList;
import java.util.Collections;
import java.util.List;/*** 赫夫曼树** @author PJ_ZHANG* @create 2020-03-26 10:36**/
public class HuffmanTree {public static void main(String[] args) {int[] array = {13, 7, 8, 3, 29, 6, 1};Node root = huffmanTree(array);preShowDetails(root);}/*** 生成赫夫曼树基本规则:* * 将数组的每个元素封装为Node, 并添加到集合中* * 对集合元素进行排序, 注意此处需要实现Comparable类, 并重写compareTo()* * 取前两个元素作为一个最简单的二叉树(不带子节点的)* * 以这两个元素作为一节点的左右两个子元素, 且该节点的权为这两个节点带权路径长度之和* * 将该父节点添加到集合中, 并对集合重新排序, 继续循环执行, 依次类推** @param array*/public static Node huffmanTree(int[] array) {// 转换为一个listList<Node> lstData = new ArrayList<>(10);for (int data : array) {lstData.add(new Node(data));}// 循环处理for (;lstData.size() > 1;) {// 对数组进行排序Collections.sort(lstData);// 获取前两个节点Node leftNode = lstData.get(0);Node rightNode = lstData.get(1);// 根据前两个节点带权路径构建第三个节点Node parentNode = new Node(leftNode.getData() + rightNode.getData());// 构建左右节点parentNode.setLeftNode(leftNode);parentNode.setRightNode(rightNode);// 移除前两个节点lstData.remove(leftNode);lstData.remove(rightNode);// 添加新构建的节点到集合中lstData.add(parentNode);}return lstData.get(0);}public static void preShowDetails(Node node) {if (null == node) {return;}System.out.print(node.getData() + "  ");if (null != node.getLeftNode()) {preShowDetails(node.getLeftNode());}if (null != node.getRightNode()) {preShowDetails(node.getRightNode());}}@Datastatic class Node implements Comparable<Node> {private int data;private Node leftNode;private Node rightNode;public Node(int data) {this.data = data;}@Overridepublic String toString() {return "Node: [data = " + data;}/*** 进行数据比较, 满足数据升序排序* @param node* @return*/@Overridepublic int compareTo(Node node) {return this.data - node.getData();}}}

2，赫夫曼编码

2.1，赫夫曼编码基本介绍

  • 赫夫曼编码也称为霍夫曼编码，是一种编码方式，属于一种程序算法
  • 赫夫曼编码是赫夫曼树在电讯通讯中的经典应用之一
  • 赫夫曼树广泛的应用于数据文件压缩，压缩率在20%~90%之间
  • 赫夫曼编码是可变字长编码（VLC）的一种，Huffman与1952年提出的一种编码方法，称为最佳编码

2.2，赫夫曼编码原理剖析

2.2.1，定长编码

  • 定长编码是将传递文本首先按照ASCII码转换为数字类型，再对数字类型二进制化后进行传递，传递的信息即为原始文本直译，流程如下：
  • 如有原始文本：

i like like like java do you like a java

  • 原始文本转换为ASCII码后如下：

105 32 108 105 107 101 32 108 105 107 101 32 108 105 107 101 32 106 97 118 97 32 100 111 32 121 111 117 32 108 105 107 101 32 97 32 106 97 118 97

  • ASCII码二进制化后如下：

01101001 00100000 01101100 01101001 01101011 01100101 00100000 01101100 01101001 01101011 01100101 00100000 01101100 01101001 01101011 01100101 00100000 01101010 01100001 01110110 01100001 00100000 01100100 01101111 00100000 01111001 01101111 01110101 00100000 01101100 01101001 01101011 01100101 00100000 01100001 00100000 01101010 01100001 01110110 01100001

  • 按照二进制传递消息，传递消息长度为 359（包括空格）

2.2.2，变长编码

  • 定长编码是对原始文本的直译，传递信息较大，因此可以用变长编码进行重组
  • 同样一串原始文本，变长编码会对文本内容进行统计，统计各个字符的个数：

// 字符统计
d:1 y:1 u:1 j:2 v:2 o:2 l:4 k:4 e:4 i:5 a:5 :9
// 二进制赋值
0= , 1=a, 10=i, 11=e, 100=k, 101=l, 110=o, 111=v, 1000=j, 1001=u, 1010=y, 1011=d

  • 字符统计完成后，根据字符所占个数，从大到小以二进制进行递增赋值。如空格出现次数最多，则赋值为0，其次是a，赋值01，再次i，赋值10，依次类推
  • 按照上面的方式，会对传递的编码进行组合，最终组合的传递文本肯定远小于定长编码
  • 但是变长编码存在问题：前缀重合。即存在部分字符的二进制表达式是其他字符的前缀，在解析中可能会存在混乱，如01和0101，不能确定是两个01还是一个完整的0101
  • 根据上面问题，提出了前缀编码概念，即字符的编码不能是其他字符编码的前缀，赫夫曼编码就是一种前缀编码

2.2.3，赫夫曼编码

  • 同变长编码，赫夫曼编码同样会统计字符所占个数，并以该个数作为节点的权值构建赫夫曼树
  • 则按照字符统计频次：d:1 y:1 u:1 j:2 v:2 o:2 l:4 k:4 e:4 i:5 a:5 :9构建的赫夫曼树如下：
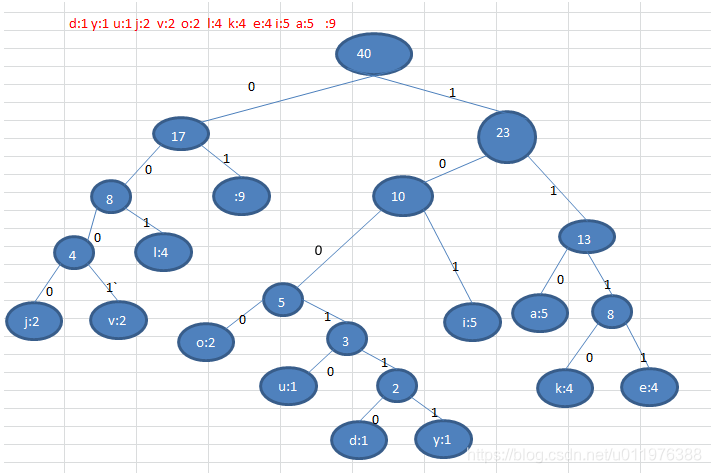
    在这里插入图片描述
  • 同时，将父节点左侧分叉定义为0，右侧分叉定义为1，每一个叶子节点所对应的赫夫曼编码为节点路径对应值的组合：

o: 1000 u: 10010 d: 100110 y: 100111 i: 101
a : 110 k: 1110 e: 1111 j: 0000 v: 0001
l: 001 : 01

  • 按照上面的赫夫曼编码，原始文本字符串对应的编译后的编码应该为：

1010100110111101111010011011110111101001101111011110100001100001110011001111000011001111000100100100110111101111011100100001100001110

  • 字符长度为 133，直译字符长度为359，压缩比例超过60%
  • 同时，生成赫夫曼树后，每一个原始数组有效节点在赫夫曼树都以叶子节点存在，所以前缀不可能重复
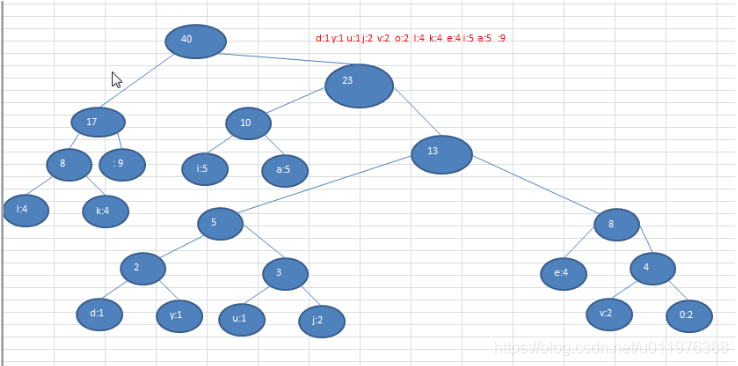
  • 最后需要注意一个问题：赫夫曼树根据排序方式不同，虽然赫夫曼树的WPL完成相等，但生成的赫夫曼树会有些许差别。比如对于权值一样的节点排序，如果存在新生成父节点与原始节点权值相等，再排序时，将父节点放在前面与放在后面生成的赫夫曼树是不一致的；以上树为例，存在另外一种赫夫曼树组合方式
    在这里插入图片描述

2.3，赫夫曼编码 — 数据压缩解压

2.3.1，数据压缩逻辑

  • 先对需要传递的文本进行字符统计，并以单个字符出现的频次进行排序
  • 对排序生成的数组构建赫夫曼树，此处注意排序方式不同，构建的数不同，但树的WPL是一致的
  • 对赫夫曼树的每一个叶子节点，即有效数据节点进行路径统计，左侧节点路径代表为0，右侧节点路径代表为1，从根节点开始，每一个叶子节点都有唯一的路径表达，且符合前缀表达式
  • 将传递文本根据ASCII码进行拆分，并将每一个字符转换为对应的路径，最终生成一个二进制数字串
  • 此时生成的二进制串是远大于需要传递的文本长度的，需要对需要传递的串每八位进行截取，并生成一个byte类型的数字，最终转换成为一个byte[]，此时这个字节数组以及上上一步生成的路径映射Map是真正需要传递出去的数据
  • 代码在解压部分一块附上

2.3.2，数据解压逻辑

  • 对于解压部分来说，解压就是顺着压缩的步骤反向走一遍
  • 首先，解压初始化入参是能接受到压缩后传递的byte[]数组和路径映射Map
  • 先对byte[]数组二进制化，转换为二进制数字串，也就是每一个ASCII字符在赫夫曼树中对应路径组成的二进制数字串
  • 然后对路径映射Map进行反转，传递的是字符 -> 路径的映射，转换为路径 -> 字符的映射，转换完成后，可以直接通过路径获取目标字符，重组数据串
  • 因为二进数数组串满足前缀表达式，所以按二进制数字串的每一个字符依次向后移动，从反转后的Map中根据截取路径获取有效字符
    • 获取到后，拼接到结果串中，并以下一个字符作为起点，继续向后截取
    • 如果获取不到，则继续扩入一个字符进行获取
    • 依次类推，直接截取到二进制数字串结尾，获取到所有有效数据

2.3.3，压缩解压代码

package com.self.datastructure.tree.huffmancode;import lombok.Data;
import org.apache.commons.collections.CollectionUtils;import java.util.*;/*** 霍夫曼编码** @author PJ_ZHANG* @create 2020-04-07 15:16**/
public class HuffmanCode {public static void main(String[] args) {String content = "i like like like java do you like a java";// 数据压缩// 先将传递字符串转换为byte数组, 并对每一种ASCII码出现频率进行统计// 根据频率大小构造赫夫曼树, 并将每一个叶子节点对应的编码值进行Map映射// 将原始字符串转换为赫夫曼编码字符串, 此时转换为一串二进制数字// 将这一串二进制数字转换为byte数组, 并准备进行传递// 最终传递需要赫夫曼树的Map映射和二进制数子串的byte数组// 路径映射,Map<Byte, String> pathMap = new HashMap<>(16);// 最终获取到的结果如下// [-88, -65, -56, -65, -56, -65, -55, 77, -57, 6, -24, -14, -117, -4, -60, -90, 28]byte[] encodeBytes = encode(content, pathMap);System.out.println("最终生成的十进制传输数据: " + Arrays.toString(encodeBytes));// 数据解压// 将传递的byte[]数组, 转换为赫夫曼编码的二进制数字串// 将二进制数组串, 对照赫夫曼编码字典, 重新转换为字符串byte[] decodeBytes = decode(encodeBytes, pathMap);System.out.println("解析内容完成: " + new String(decodeBytes));}/*** 反编译文本内容* 反编译文本内容与编译文本内容相反** @param encodeBytes 传递的十进制数字串* @param pathMap 字符到频次映射* @return*/private static byte[] decode(byte[] encodeBytes, Map<Byte, String> pathMap) {// 首先转换十进制传递数组为二进制数字串// 反编译的二进制串: 1010100010111111110010001011111111001000101111111100100101001101110001110000011011101000111100101000101111111100110001001010011011100String binaryStr = decodeBinaryStr(encodeBytes);// 转换二进制数字串为原始字符的字节数组byte[] bytes = decodeContent(binaryStr, pathMap);return bytes;}/*** 反编译二进制数字串成功后, 开始进行截取映射字典, 生成byte数组, 以便后续进行文本解析** @param binaryStr 二进制数字串* @param pathMap 字符和路径映射* @return*/private static byte[] decodeContent(String binaryStr, Map<Byte, String> pathMap) {// 反转字符和路径映射, 处理为路径映射字符Map<String, Byte> path2ByteMap = reverseMap(pathMap);// 根据路径一段段截取二进制数字串, 并拼凑为有效的byte码byte[] resultBytes = doDecodeContent(binaryStr, path2ByteMap);return resultBytes;}/*** 反编译为最终需要的字节码* @param binaryStr 二进制自己串* @param path2ByteMap 路径到字符的映射* @return*/private static byte[] doDecodeContent(String binaryStr, Map<String, Byte> path2ByteMap) {// 截取的每一个数字, 添加到集合中List<Byte> lstBytes = new ArrayList<>(10);for (int i = 0; i < binaryStr.length();) {int count = 1;for (;;) {// 以count作为一个标识位, 一直向后移动, 多括进一个字符// 如果路径到字符映射中, 包含该路径, 则匹配成功, 并添加该字符到集合String currStr = binaryStr.substring(i, i + count);if (null != path2ByteMap.get(currStr)) {// 添加字符到集合中lstBytes.add(path2ByteMap.get(currStr));break;}count++;}// 匹配成功后, i直接进count位, 进行下一组数据处理i += count;}// 转换集合为数组byte[] bytes = new byte[lstBytes.size()];int index = 0;for (Byte currByte : lstBytes) {bytes[index++] = currByte;}return bytes;}/*** 反转字符串, 反转为<value, key>形式** @param pathMap* @return*/private static Map<String,Byte> reverseMap(Map<Byte, String> pathMap) {Map<String, Byte> path2ByteMap = new HashMap<>(16);for (Map.Entry<Byte, String> entry : pathMap.entrySet()) {path2ByteMap.put(entry.getValue(), entry.getKey());}return path2ByteMap;}/*** 反编译为二进制数字串* @param encodeBytes 十进制字符* @return 二进制数字串*/private static String decodeBinaryStr(byte[] encodeBytes) {StringBuilder sb = new StringBuilder();boolean isNeedSub = true;for (int i = 0; i < encodeBytes.length; i++) {if (i == encodeBytes.length - 1 && encodeBytes[i] > 0) {isNeedSub = false;}sb.append(decodeDecimal(isNeedSub, encodeBytes[i]));}return sb.toString();}/*** 转换* @param isNeedSub 是否需要截取* @param encodeByte 当前需要转换的数据* @return*/private static String decodeDecimal(boolean isNeedSub, int encodeByte) {String str = "";// 此处负数通过二进制转换会转换为标准的32位, 但是正数不会补0// 所以需要对数据转换后再截取, 转换方式为与256进行或运算// 256的二进制为: 1 0000 0000, 无论任务数字与256进行或运算后, 绝对能保证第九位的1, 则后八位有效// 转换完成后, 截取后八位作为有效数据// 注意: 最后一位需要处理的数据不一定满8位, 所以不满八位的情况下一定为正数, 需要原样处理// 满八位后, 可能为负数, 需要进行判断是否截取, 在调用方法中已经加标识位判断if (isNeedSub) {encodeByte |= 256;str = Integer.toBinaryString(encodeByte);str = str.substring(str.length() - 8);} else {str = Integer.toBinaryString(encodeByte);}return str;}/*** 编译文本内容** @param content 文本内容* @param pathMap 字符Byte到赫夫曼码的映射* @return*/private static byte[] encode(String content, Map<Byte, String> pathMap) {// 获取到字节码byte[] bytes = content.getBytes();// 统计频次, 以频次作为构建赫夫曼节点的权值Map<Byte, Integer> timeMap = new HashMap<>(16);statisticsTime(bytes, timeMap);// 转换频次映射Map为ListList<Node> lstNode = transformMap2List(timeMap);// 转换为赫夫曼树Node huffmanTree = encodeHuffmanTree(lstNode);// 根据赫夫曼树, 生成字符的映射路径encodeByte2Path(huffmanTree, pathMap);// 根据传递内容, 拼接赫夫曼编码的二进制串, 按照上面传递的字符, 长度应该为133// 另外不同方式方式构建的赫夫曼树, 获得的串不一致// 比如形同time值的不同数据, 放在list的不同位置, 拼出来的树不一样, 但带权路径一样String binaryStr = encodeBinaryStr(bytes, pathMap);// 构建完成二进制串后, 对二进制串每8位生成一个十进制数据进行传递, 并转换为byte// 此处主要为了减少传递数据byte[] resultData = encodeResultData(binaryStr);return resultData;}/*** 对二进制数字串, 每8位构造一个十进制数据, 并传递出去,* 这一步构造的数据, 是真正需要传递出去的数据** @param binaryStr* @return*/private static byte[] encodeResultData(String binaryStr) {// 获取长度int length = (binaryStr.length() + 7) / 8;int count = 0;int index = 0;byte[] bytes = new byte[length];// 截取长度进行处理for (int i = 0; i < length; i++) {String currStr = "";if (i == length - 1) {currStr = binaryStr.substring(count);} else {currStr = binaryStr.substring(count, count + 8);count += 8;}// 截取完成后, 转为byte型byte currData = (byte) Integer.parseInt(currStr, 2);bytes[index++] = currData;}return bytes;}/*** 拼接二进制数字串* @param bytes 传递字符串转换后的byte* @param pathMap byte到二进制路径的映射* @return*/private static String encodeBinaryStr(byte[] bytes, Map<Byte, String> pathMap) {StringBuilder sb = new StringBuilder();for (byte b : bytes) {sb.append(pathMap.get(b));}return sb.toString();}/*** 根据赫夫曼树, 构建路径映射** @param huffmanTree 赫夫曼树* @param pathMap 路径映射*/private static void encodeByte2Path(Node huffmanTree, Map<Byte, String> pathMap) {StringBuilder sb = new StringBuilder();if (null != huffmanTree.getLeftNode()) {// 左侧拼接0appendPath(huffmanTree.getLeftNode(), "0", sb, pathMap);}if (null != huffmanTree.getRightNode()) {// 右侧拼接1appendPath(huffmanTree.getRightNode(), "1", sb, pathMap);}}/*** 拼接路径** @param node 当前节点* @param pathCode 路径值* @param sb 拼接字符* @param pathMap 映射字符*/private static void appendPath(Node node, String pathCode, StringBuilder sb, Map<Byte, String> pathMap) {StringBuilder newSB = new StringBuilder(sb);newSB.append(pathCode);if (null != node.getLeftNode()) {appendPath(node.getLeftNode(), "0", newSB, pathMap);}if (null != node.getRightNode()) {appendPath(node.getRightNode(), "1", newSB, pathMap);}// 遍历只处理叶子节点, 生成的虚拟父节点, data值为nullif (null != node.getData()) {pathMap.put(node.getData(), newSB.toString());}}/*** 转换为赫夫曼树** @param lstNode 构造的字符节点集合* @return 赫夫曼树根节点*/private static Node encodeHuffmanTree(List<Node> lstNode) {for (;CollectionUtils.isNotEmpty(lstNode) && lstNode.size() > 1;) {// 每一次循环排序一次, 保证取到的前两个二叉树为最小数据Collections.sort(lstNode);// 构造父节点, 并设置左右子节点Node leftNode = lstNode.get(0);Node rightNode = lstNode.get(1);Node parentNode = new Node();parentNode.setTime((byte) (leftNode.getTime() + rightNode.getTime()));parentNode.setLeftNode(leftNode);parentNode.setRightNode(rightNode);// 从集合中移除前两个节点lstNode.remove(leftNode);lstNode.remove(rightNode);// 添加新节点lstNode.add(parentNode);}return lstNode.get(0);}/*** 转换映射频次为List, 方便后续赫夫曼树转换** @param timeMap* @return*/private static List<Node> transformMap2List(Map<Byte, Integer> timeMap) {List<Node> lstNode = new ArrayList<>(10);for (Map.Entry<Byte, Integer> entry : timeMap.entrySet()) {Node node = new Node(entry.getKey(), entry.getValue());lstNode.add(node);}return lstNode;}/*** 统计每一个字符出现的频次** @param bytes* @param pathMap*/private static void statisticsTime(byte[] bytes, Map<Byte, Integer> timeMap) {for (byte currByte : bytes) {Integer time = timeMap.get(currByte);time = null == time ? 1 : ++time;timeMap.put(currByte, time);}}@Datastatic class Node implements Comparable<HuffmanCode.Node> {private Byte data; // 字符private int time; // 字符频次private Node leftNode;private Node rightNode;public Node(Byte data, int time) {this.data = data;this.time = time;}@Overridepublic String toString() {return "Node: [data = " + data + ", time = " + time + "] ";}/*** 进行数据比较, 满足数据升序排序* @param node* @return*/@Overridepublic int compareTo(Node node) {return this.getTime() - node.getTime();}}}

2.4，赫夫曼编码 — 文件压缩解压

2.4.1，文件压缩逻辑

  • 赫夫曼编码是基于字节数组进行编码，编码为二进制数字串后再转换为字节数组进行输出
  • 因为所有文件都可以通过输入流转换为字节数组，所以在理论上是都可以通过赫夫曼编码进行压缩的
  • 将原始文件读到内存中经过赫夫曼编码逻辑生成路径映射Map及赫夫曼编码的字节数组，并将这两个对象写入目标文件即为压缩后的文件
  • 代码在解压中附上

2.4.2，文件解压逻辑

  • 接文件压缩，文件压缩将路径映射Map及赫夫曼编码的字节数组写入压缩文件，再文件解压时需要读取文件内这两部分内容
  • 读取到两个对象后，通过赫夫曼编码解压部分代码进行内容解析，解析生成一个原始文件对应的byte[]
  • 将这个byte[]对象直接通过输出流输出为一个新文件，即文件解压

2.4.3，压缩解压代码

package com.self.datastructure.tree.huffmancode;import java.io.*;
import java.util.HashMap;
import java.util.Map;/*** 文件压缩_赫夫曼编码** @author PJ_ZHANG* @create 2020-04-08 11:24**/
public class FileHuffmanCode {public static void main(String[] args) {// 文件压缩// 首先压缩方式与文本基本一致, 读取到文件的所有字节码后// 构造赫夫曼树, 生成路径映射// 构造二进制数字串之后转为byte[]数组// 写出byte[]数组和路径映射到文件中, 该文件即为压缩文件compress("F:\\123.bmp", "F:\\123.zip");System.out.println("压缩完成...");// 文件解压// 解压是先从第一布的压缩文件路径中读取到写出的byte[]数组和路径映射// 之后对byte[]数组进行二进制数字串转换再多最后的源文件字节数组转换// 最后写出字节数组到目标文件中, 视为对压缩文件的解压decompress("F:\\123.zip", "F:\\1234.bmp");System.out.println("解压完成...");}/*** 文件解压** @param srcFilePath* @param desFilePath*/private static void decompress(String srcFilePath, String desFilePath) {FileInputStream is = null;ObjectInputStream ois = null;FileOutputStream os = null;try {is = new FileInputStream(srcFilePath);ois = new ObjectInputStream(is);// 按顺序读取赫夫曼码映射和赫夫曼编码转换后的字节数组Map<Byte, String> pathMap = (Map<Byte, String>) ois.readObject();byte[] bytes = (byte[]) ois.readObject();// 解压为真是的字节数组byte[] needBytes = ContentHuffmanCode.decode(bytes, pathMap);// 写出去os = new FileOutputStream(desFilePath);os.write(needBytes);os.flush();} catch (Exception e) {e.printStackTrace();} finally {try {is.close();ois.close();os.close();} catch (Exception e) {e.printStackTrace();}}}/*** 文件压缩** @param srcFilePath 文件源路径* @param desFilePath 文件目标路径*/private static void compress(String srcFilePath, String desFilePath) {// 初始化输入输出流FileInputStream is = null;FileOutputStream os = null;ObjectOutputStream oos = null;try {// 读取文件字节码is = new FileInputStream(srcFilePath);byte[] bytes = new byte[is.available()];is.read(bytes);// 构造赫夫曼编码路径映射及转换后的字节码Map<Byte, String> pathMap = new HashMap<>(16);byte[] huffmanBytes = ContentHuffmanCode.encode(bytes, pathMap);// 写数据到目标文件中, 作为压缩文件os = new FileOutputStream(desFilePath);oos = new ObjectOutputStream(os);oos.writeObject(pathMap);oos.writeObject(huffmanBytes);oos.flush();} catch (Exception e) {e.printStackTrace();} finally {try {is.close();os.close();oos.close();} catch (IOException e) {e.printStackTrace();}}}}

这篇关于树：赫夫曼树赫夫曼编码的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/1079978。

相关文章

C++ | Leetcode C++题解之第393题UTF-8编码验证

C++ | Leetcode C++题解之第393题UTF-8编码验证

题目： 题解： class Solution {public:static const int MASK1 = 1 << 7;static const int MASK2 = (1 << 7) + (1 << 6);bool isValid(int num) {return (num & MASK2) == MASK1;}int getBytes(int num) {if ((num &
阅读更多...
C语言 | Leetcode C语言题解之第393题UTF-8编码验证

C语言 | Leetcode C语言题解之第393题UTF-8编码验证

题目： 题解： static const int MASK1 = 1 << 7;static const int MASK2 = (1 << 7) + (1 << 6);bool isValid(int num) {return (num & MASK2) == MASK1;}int getBytes(int num) {if ((num & MASK1) == 0) {return
阅读更多...
form表单提交编码的问题

form表单提交编码的问题

浏览器在form提交后，会生成一个HTTP的头部信息"content-type"，标准规定其形式为Content-type: application/x-www-form-urlencoded; charset=UTF-8        那么我们如果需要修改编码，不使用默认的，那么可以如下这样操作修改编码，来满足需求： hmtl代码：   <meta http-equiv="Conte
阅读更多...
4-4.Andorid Camera 之简化编码模板（获取摄像头 ID、选择最优预览尺寸）

4-4.Andorid Camera 之简化编码模板（获取摄像头 ID、选择最优预览尺寸）

一、Camera 简化思路 在 Camera 的开发中，其实我们通常只关注打开相机、图像预览和关闭相机，其他的步骤我们不应该花费太多的精力 为此，应该提供一个工具类，它有处理相机的一些基本工具方法，包括获取摄像头 ID、选择最优预览尺寸以及打印相机参数信息 二、Camera 工具类 CameraIdResult.java public class CameraIdResult {
阅读更多...
Python字符编码及应用

Python字符编码及应用

字符集概念 字符集就是一套文字符号及其编码的描述。从第一个计算机字符集ASCII开始，为了处理不同的文字，发明过几百种字符集，例如ASCII、USC、GBK、BIG5等，这些不同的字符集从收录到编码都各不相同。在编程中出现比较严重的问题是字符乱码。 几个概念 位：计算机的最小单位二进制中的一位，用二进制的0，1表示。 字节：八位组成一个字节。（位与字节有对应关系） 字符：我们肉眼可见的文字与符号。
阅读更多...
在Eclipse环境下修改Tomcat编码的问题

在Eclipse环境下修改Tomcat编码的问题

问题： 由于BMS需要设置UTF-8编码，要不就会出现中文乱码问题； 一、项目保持UTF-8格式； 二、由于可能会多次移除项目、加载项目，不想每次都要修改tmp0\conf 原因： 如果在eclipse中配置了tomcat后，其实，tomcat所用的所有tomcat配置文件，都不是catalina_home/config下面的xml文件，而是在eclipse所创建的Serve
阅读更多...
在Unity环境中使用UTF-8编码

在Unity环境中使用UTF-8编码

为什么要讨论这个问题         为了避免乱码和更好的跨平台         我刚开始开发时是使用VS开发,Unity自身默认使用UTF-8 without BOM格式,但是在Unity中创建一个脚本,使用VS打开,VS自身默认使用GB2312(它应该是对应了你电脑的window版本默认选取了国标编码,或者是因为一些其他的原因)读取脚本,默认是看不到在VS中的编码格式,下面我介绍一种简单快
阅读更多...
霍夫曼编码/译码器

霍夫曼编码/译码器

赫夫曼树的应用 1、哈夫曼编码 　　在数据通信中，需要将传送的文字转换成二进制的字符串，用0，1码的不同排列来表示字符。例如，需传送的报文为“AFTER DATA EAR ARE ART AREA”，这里用到的字符集为“A，E，R，T，F，D”，各字母出现的次数为{8，4，5，3，1，1}。现要求为这些字母设计编码。要区别6个字母，最简单的二进制编码方式是等长编码，固定采用3位二进制，可分别用
阅读更多...
Base64编码 及 在HTML中用Base编码直接显示图片或嵌入其他文件类型

Base64编码 及 在HTML中用Base编码直接显示图片或嵌入其他文件类型

1.为什么要用到BASE64编码的图片信息      Base64是网络上最常见的用于传输8Bit字节代码的编码方式之一。Base64 主要不是加密，它主要的用途是把一些二进制数转成普通字符用于网络传输。由于一些二进制字符在传输协议中属于控制字符，不能直接传送需要转换一下。最常见的用途是作为电子邮件或WebService附件的传输编码.  2.base64编码定义  　　目前的internet
阅读更多...
批量文件编码转换用python实现的utf8转gb2312,vscode设置特殊文件的默认打开编码

批量文件编码转换用python实现的utf8转gb2312,vscode设置特殊文件的默认打开编码

批量文件编码转换用python实现的utf8转gb2312, 任意编码之间的相互转换都是可以的.改一下下面的参数即可 convert.py文件内容如下 import osimport globimport chardet#检测文件编码类型def detect_file_encoding(file_path):with open(file_path, 'rb') as f:data = f
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2