归并排序的应用—计算逆序对的个数

本文主要是介绍归并排序的应用—计算逆序对的个数，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

归并排序的应用—计算逆序对的个数

- 什么是逆序对
- 题目的思路
题目

如果你还不会归并排序，那么请你先学会它，再来看本篇文章效果更佳。

什么是逆序对

逆序对的定义：在一个数列中，如果前面的数字大于后面的数字，那么这两个数字就构成了一个逆序对。

在这里插入图片描述

比如数列是这样的。

如果找数字4 能够匹配成的逆序对，那么就有下列的这几对

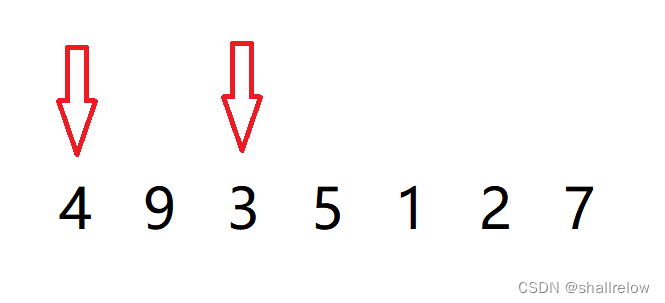
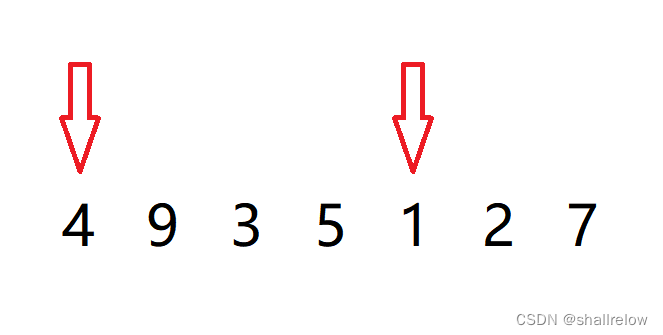
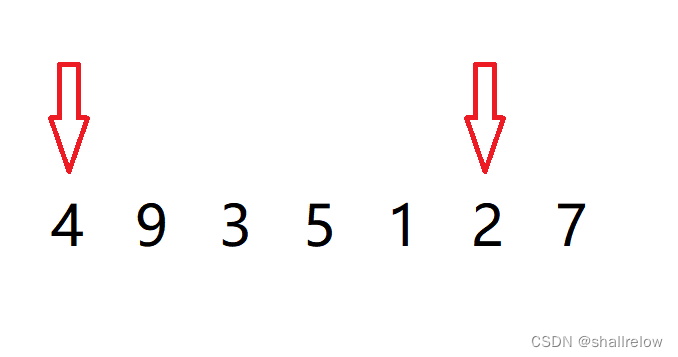
在这里插入图片描述

在这里插入图片描述
如果找数字 9 匹配的，那么它后面的数字都比9小，所以后面的数字都可以和9组成逆序对。

题目的思路

在讲解题目之前我们需要知道一个理论知识。

在这里插入图片描述
假设我们有两组序列。

其中红色区域内的数字无论怎么在红色区域内部 “动”，绿色区域内与它匹配的逆序对都不会改变。

比如红色区域有一个 9，那么它在红色区域内的任意一个地方，绿色区域与它匹配的逆序对的数量都是固定的。

接着我们还需要一个理论知识。

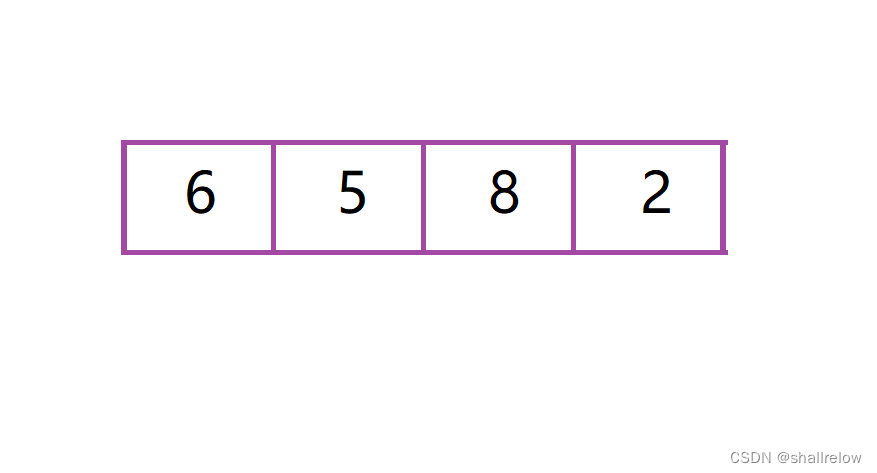
在这里插入图片描述
比如我需要算这个序列的逆序对。

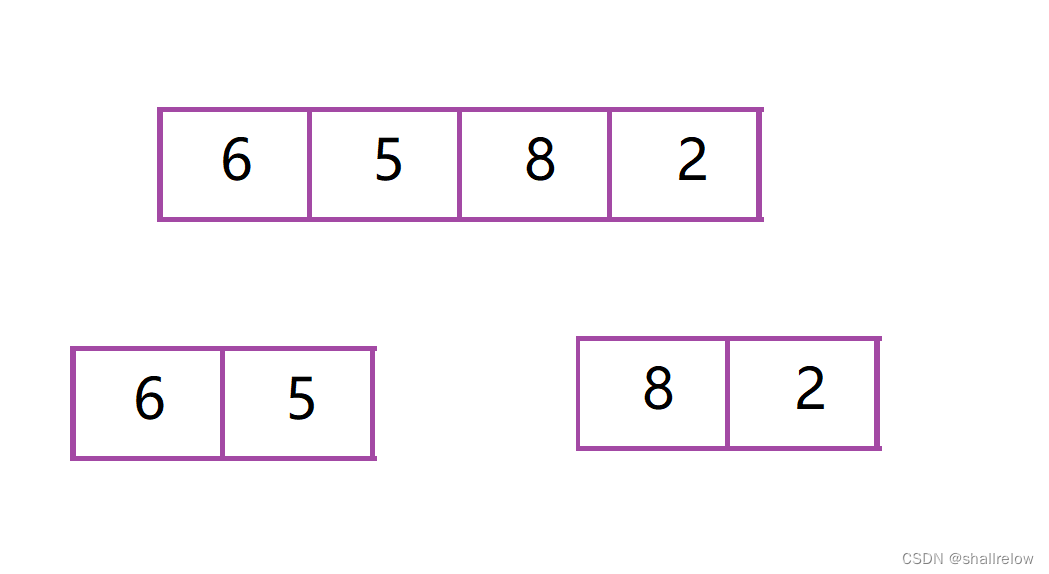
在这里插入图片描述
我们可以分别计算这两个区间内部的逆序对。

很明显都是1。

在算完了 6 和 5 的逆序对后，这两个数字的位置就可以任意更换了，2 和 8 也同理。

怎么变都不会影响，它们与其他区间的逆序对。

所以我们可以让他们都变为一个有序的序列。
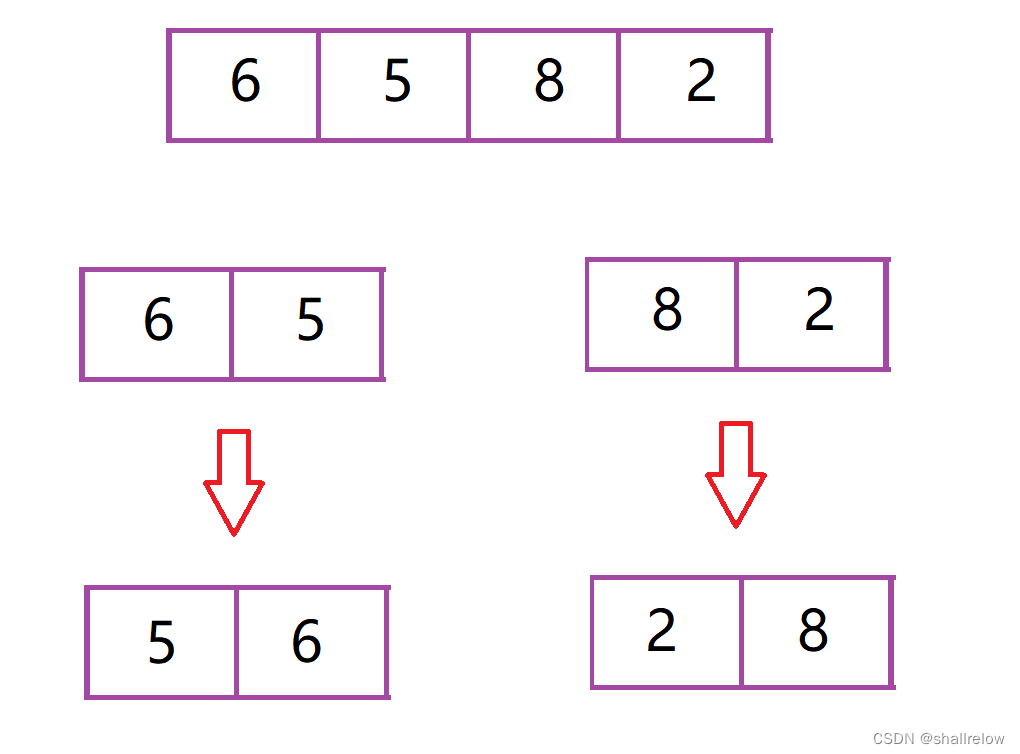
在这里插入图片描述
接着我们需要知道两个有序数列怎么求它们的逆序对的个数。

还记得我们归并排序中 “合” 的过程吗？

我们需要通过一个临时数组来达到排序的效果。

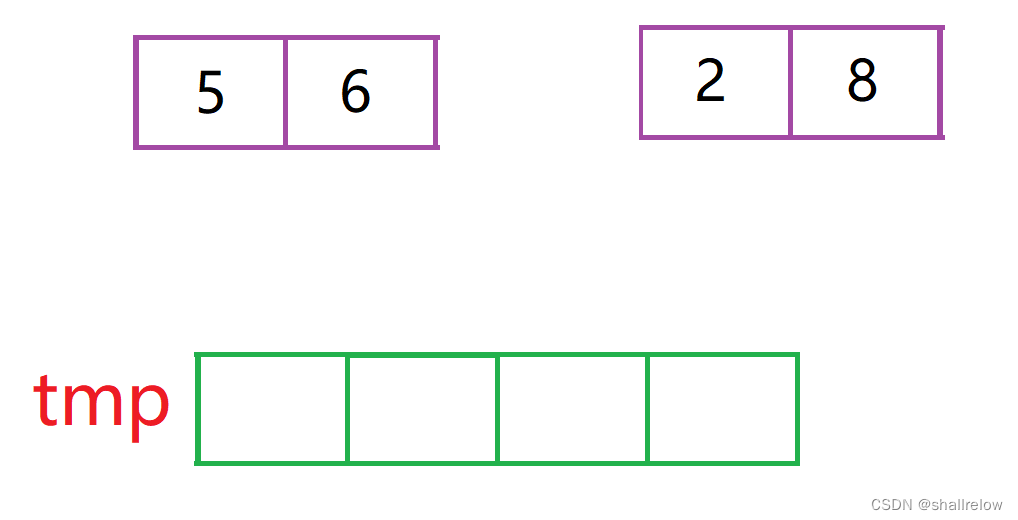
在这里插入图片描述
也就是在这个过程，就是计算逆序对个数的核心。

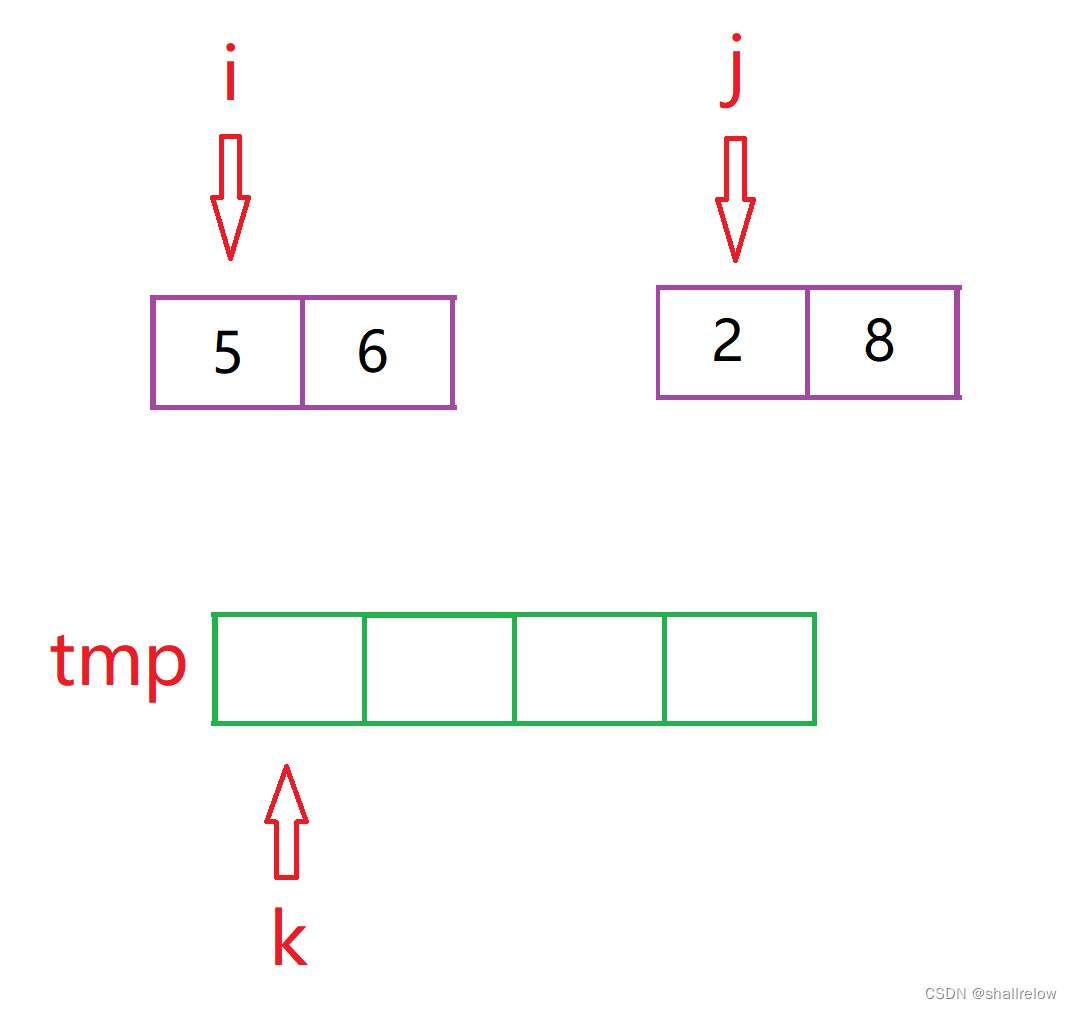
在这里插入图片描述
归并排序中合的时候会比较下标i 和 j 的值，小的放在临时数组中。。

此时如果是右边的序列，也就是 j 的那边如果小了，那么此时 i 到右边区间尾的这段数字都会比此时的 j 下标的数字要小。

比如此时图中的 2会放到临时数组中。

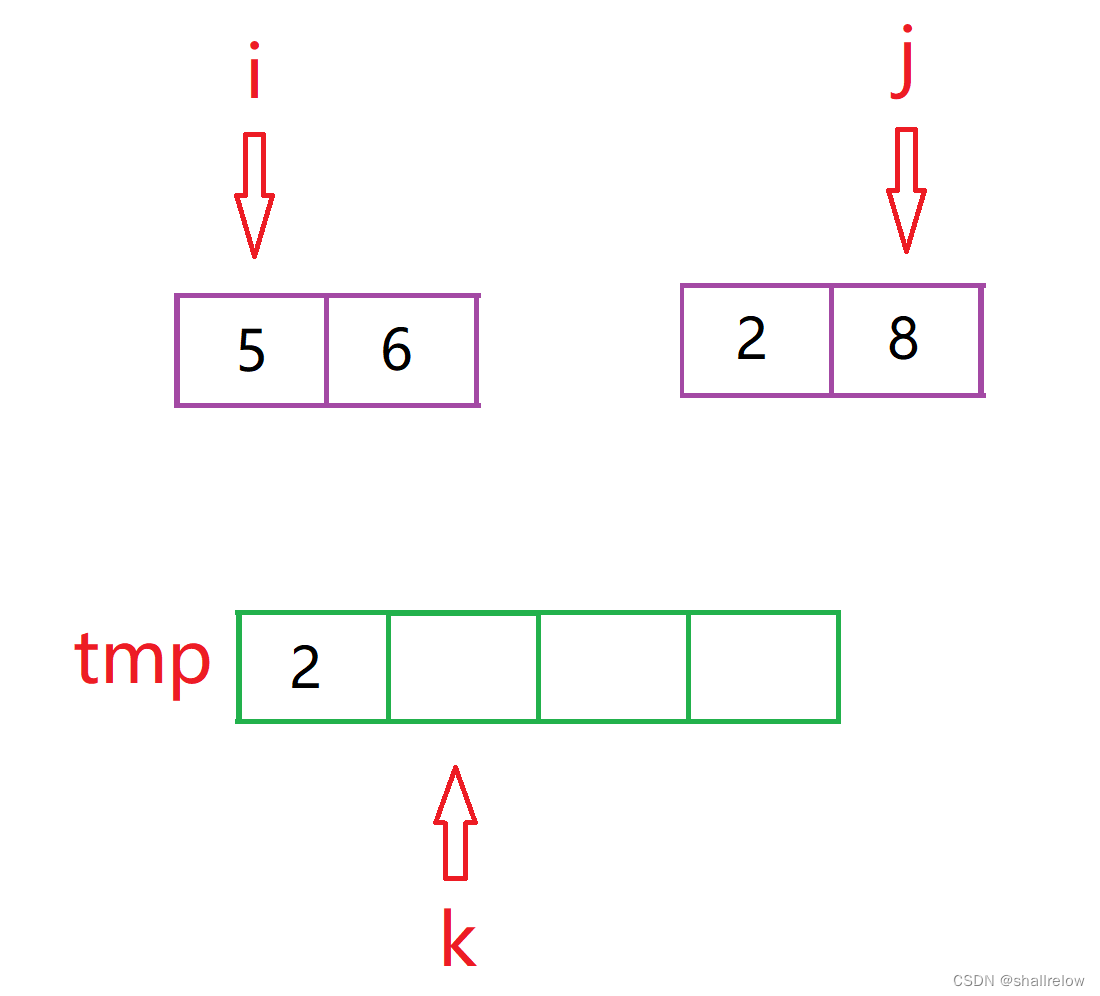
在这里插入图片描述
此时就说明了，下标 i 的数字及后面的数字一定是比 2 要大的，那么这些数字都可以和 2 组成逆序对。

此时逆序对的数量应该是 mid - i + 1。
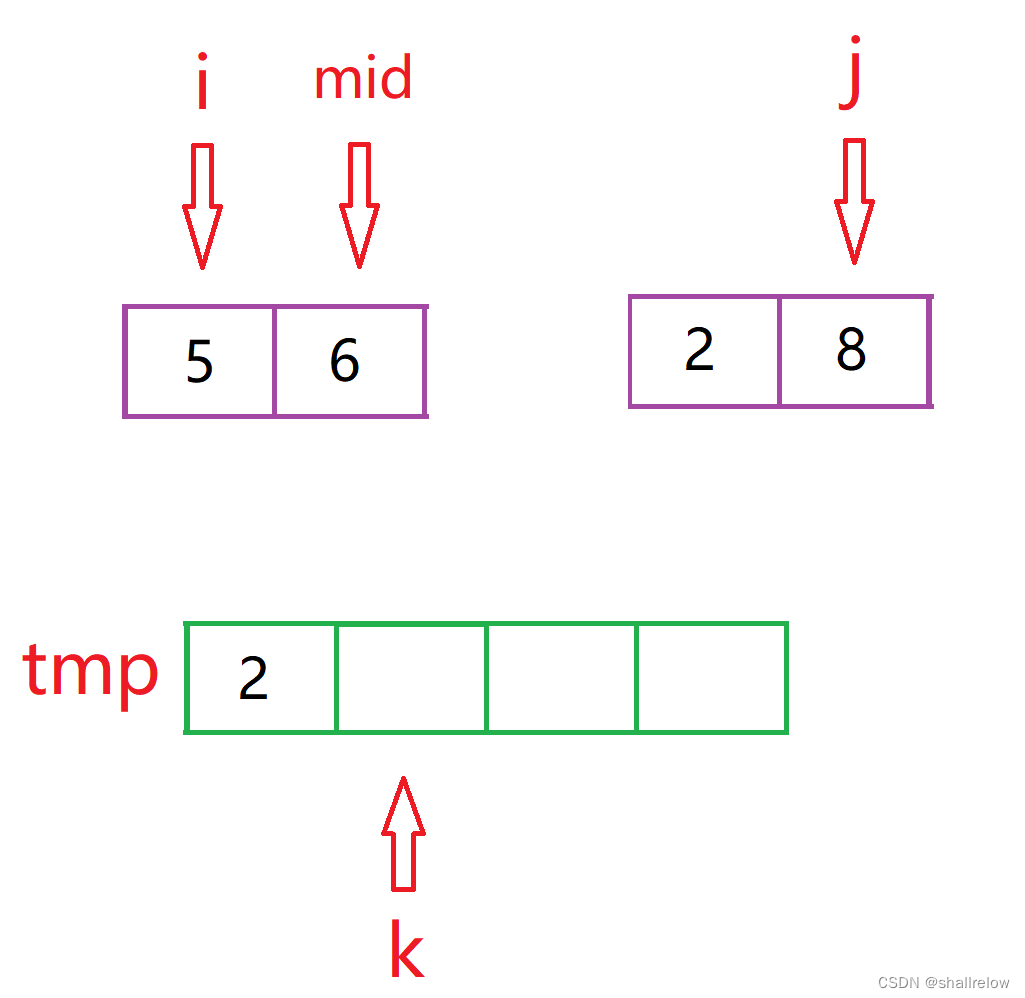
在这里插入图片描述

因为 mid 指向的是左边最后一个下标，mid - i + 1 就是 i ~ mid 的数量。

综上所述，就是在归并排序当中合并两个有序的序列时，计算逆序对的个数；由于排完序是不影响局部对外界的逆序对数量，所以两个序列是一定有序的。

接下来我们来转换成代码。

题目

给定一个长度为 $n$ 的整数数列，请你计算数列中的逆序对的数量。

逆序对的定义如下：对于数列的第 $i$ 个和第 $j$ 个元素，如果满足 $i < j$ 且 $a [i] > a [j]$ ，则其为一个逆序对；否则不是。

输入格式

第一行包含整数 $n$ ，表示数列的长度。

第二行包含 $n$ 个整数，表示整个数列。

输出格式

输出一个整数，表示逆序对的个数。

数据范围

$\le n \le 100000$ ，
数列中的元素的取值范围 $1,10^9]$ 。

输入样例：

6
2 3 4 5 6 1

输出样例：

准备阶段：
在这里插入图片描述

相比于归并排序，这里需要多个计数器。

在这里插入图片描述
相比于归并排序，最后输出cnt即可。

在这里插入图片描述
其中归并排序里面到这里都与单纯的归并排序一样。

在这里插入图片描述
在合的过程中，只比单纯的归并排序多了一句话。

就是当 j 下标的数字小的时候，此时 i 下标到mid 下标的数字都一定比刚才j下标的值要大，也就有这么多的逆序对的数量。

最后还需要注意一个问题，就是数据如果太大的话，int cnt 会存不下，所以我们改成 long。

完整代码如下：

#include <iostream>
using namespace std;const int N = 1e5+10;
int n;
int a[N], tem[N];
long cnt;void merge_sort(int q[], int l, int r)
{if (l >= r) return;int mid = (l + r) >> 1;merge_sort(q, l, mid);merge_sort(q, mid + 1, r);int i = l, j = mid + 1, k = 0;while (i <= mid && j <= r){if (q[i] <= q[j]) tem[k++] = q[i++];else{tem[k++] = q[j++];cnt += mid - i + 1;}}while (i <= mid) tem[k++] = q[i++];while (j <= r) tem[k++] = q[j++];for (int i = l, k = 0; i <= r; i++, k++) q[i] = tem[k];
}int main()
{scanf("%d", &n);for (int i = 0; i < n; i++) scanf("%d", &a[i]);merge_sort(a, 0, n - 1);printf("%ld", cnt);return 0;
}

另一种利用函数返回值的方法如下：

#include <iostream>
using namespace std;long long getCount(int q[], int l, int r)
{//递归的结束条件if (l >= r) return 0;int mid = l + r >> 1;long long cnt = 0;cnt += getCount(q, l, mid);cnt += getCount(q, mid+1, r);int temp[r-l+1];//合并int i = l, j = mid+1, k = 0;while (i <= mid && j <= r){if (q[i] <= q[j]) temp[k++] = q[i++];else{temp[k++] = q[j++];cnt += mid - i + 1;}}while (i <= mid) temp[k++] = q[i++];while (j <= r) temp[k++] = q[j++];for (i = l, j = 0; i <= r; i++, j++)q[i] = temp[j];return cnt;
}int main()
{int n;cin >> n;int arr[n];for (int i = 0; i < n; i++) cin >> arr[i];long long ret = getCount(arr, 0, n - 1);cout << ret;return 0;
}

完

这篇关于归并排序的应用—计算逆序对的个数的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！