遗传算法浅理解

本文主要是介绍遗传算法浅理解，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1. 什么是遗传算法？

遗传算法，又称为 Genetic algorithm(GA)Genetic algorithm(GA)。其主要思想就是模拟生物的遗传与变异。它的用途非常广泛，可以用于加速某些求最大或者最小值的算法（换句话说就是加速算法收敛，最主要的还是要有一个合适的目标函数，其实和现有的模型算法差不多，只不过现有的是通过不同的数据样本来进行学习收敛，而遗传算法是通过自己对样本进行变化，从而学习收敛）。

遗传算法模拟了自然选择的过程。那些适应环境的个体能够存活下来并且繁殖后代。那些不适应环境的个体将被淘汰。换言之，如果我们对每个个体都有一个适应度评分（用来评价其是否适应环境），那么对于适应度高的物体来说，将具有更高的繁殖和生存的机会。

2. 为什么叫做遗传算法？

遗传算法之所以被称为“遗传”算法，是因为它模仿了生物进化过程中的遗传机制，包括选择（自然选择）、交叉（有性繁殖）和变异（基因突变）。这些机制在生物学中决定了物种的遗传特征如何在代际之间传递和变化。

主要是进行了自交或者交配的过程来筛选收敛更快的后代。

3. 遗传算法在实际中怎么应用？

密码破解：遗传算法可以用来尝试不同的密码组合，直到找到正确的密码。虽然这听起来有点黑客的感觉，但实际上，它更多用于帮助用户找回遗忘的密码。
游戏AI：在电子游戏中，遗传算法可以用来训练AI玩家，让它们学习如何在游戏中做出最优决策。
交通路线规划：如果你是一个出租车司机，遗传算法可以帮助你找到从一个地方到另一个地方的最短路线，尤其是在交通状况复杂多变的情况下。
网站优化：遗传算法可以用来优化网站的布局，比如广告的放置位置，以提高点击率和收益。
产品设计：在设计新产品时，遗传算法可以帮助设计师在众多设计方案中找到最优解，比如设计更省油的汽车或者更舒适的椅子。
艺术创作：甚至在艺术领域，遗传算法也被用来创作音乐和艺术作品，通过不断迭代生成新的设计。
农业种植：遗传算法可以帮助农民决定种植哪些作物，以及如何安排种植时间，以最大化产量。
电力系统调度：在电力供应中，遗传算法可以优化发电和供电计划，确保电力供应既经济又可靠。
体育训练：在体育训练中，遗传算法可以帮助教练制定训练计划，比如运动员的训练强度和频率。
个人理财：遗传算法还可以用来帮助个人进行投资组合的优化，找到风险和收益的最佳平衡点。

4. 遗传算法的例子

为更好地理解遗传算法的运算过程，下面用手工计算来简单地模拟遗传算法的各
个主要执行步骤。

例：求下述二元函数的最大值：

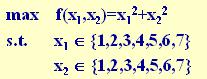
(1) 个体编码
遗传算法的运算对象是表示个体的符号串，所以必须把变量 x1, x2 编码为一种
符号串。本题中，用无符号二进制整数来表示。
因 x1, x2 为 0 ~ 7之间的整数，所以分别用3位无符号二进制整数来表示，将它
们连接在一起所组成的6位无符号二进制数就形成了个体的基因型，表示一个可
行解。
例如，基因型 X＝101110 所对应的表现型是：x＝[ 5，6 ]。
个体的表现型x和基因型X之间可通过编码和解码程序相互转换。

(2) 初始群体的产生
遗传算法是对群体进行的进化操作，需要给其淮备一些表示起始搜索点的初始
群体数据。
本例中，群体规模的大小取为4，即群体由4个个体组成，每个个体可通过随机
方法产生。
如：011101，101011，011100，111001

(3) 适应度汁算
遗传算法中以个体适应度的大小来评定各个个体的优劣程度，从而决定其遗传
机会的大小。
本例中，目标函数总取非负值，并且是以求函数最大值为优化目标，故可直接
利用目标函数值作为个体的适应度。

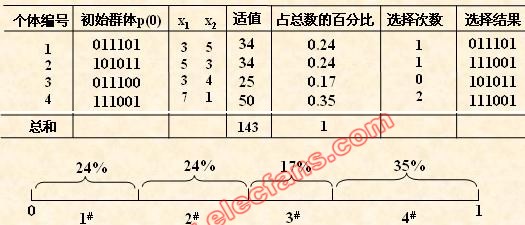
(4) 选择运算
选择运算(或称为复制运算)把当前群体中适应度较高的个体按某种规则或模型遗传到下一代群体中。一般要求适应度较高的个体将有更多的机会遗传到下一代
群体中。
本例中，我们采用与适应度成正比的概率来确定各个个体复制到下一代群体中
的数量。其具体操作过程是：
• 先计算出群体中所有个体的适应度的总和 fi ( i=1.2,…,M );
• 其次计算出每个个体的相对适应度的大小 fi / fi ，它即为每个个体被遗传
到下一代群体中的概率，
• 每个概率值组成一个区域，全部概率值之和为1；
• 最后再产生一个0到1之间的随机数，依据该随机数出现在上述哪一个概率区
域内来确定各个个体被选中的次数。

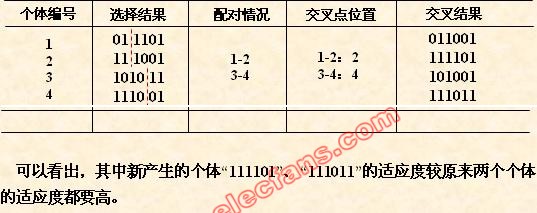
(5) 交叉运算
交叉运算是遗传算法中产生新个体的主要操作过程，它以某一概率相互交换某
两个个体之间的部分染色体。
本例采用单点交叉的方法，其具体操作过程是：
• 先对群体进行随机配对；
• 其次随机设置交叉点位置；
• 最后再相互交换配对染色体之间的部分基因。

(6) 变异运算
变异运算是对个体的某一个或某一些基因座上的基因值按某一较小的概率进
行改变，它也是产生新个体的一种操作方法。
本例中，我们采用基本位变异的方法来进行变异运算，其具体操作过程是：
• 首先确定出各个个体的基因变异位置，下表所示为随机产生的变异点位置，
其中的数字表示变异点设置在该基因座处；
• 然后依照某一概率将变异点的原有基因值取反。

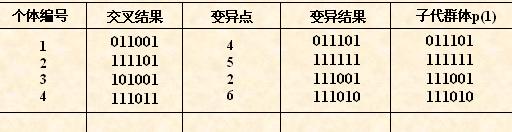
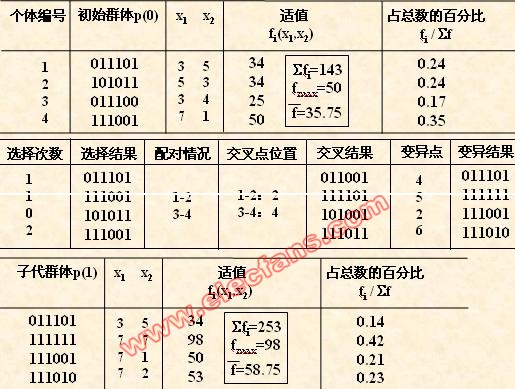
对群体P(t)进行一轮选择、交叉、变异运算之后可得到新一代的群体p(t+1)。

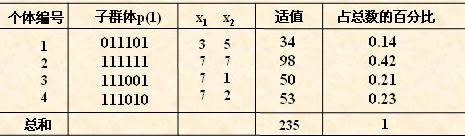
从上表中可以看出，群体经过一代进化之后，其适应度的最大值、平均值都得
到了明显的改进。事实上，这里已经找到了最佳个体“111111”。
[注意]
需要说明的是，表中有些栏的数据是随机产生的。这里为了更好地说明问题，
我们特意选择了一些较好的数值以便能够得到较好的结果，而在实际运算过程中
有可能需要一定的循环次数才能达到这个最优结果。