本文主要是介绍为什么电源滤波器中的电容器太大,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
所有 AC-DC 转换器,无论是线性电源还是具有某种开关元件,都需要一种机制来获取交流侧的变化功率并在直流侧产生恒定功率。通常,大滤波电容器用于在交流功率高于直流负载所需时吸收和存储能量,并在交流功率低于所需时向负载提供能量。图 1 是表示交流线路频率为 \[\omega\] 的通用 AC-DC 转换器的功率输入和功率输出的框图。无论转换器模块内部的具体情况如何,所有转换器都将具有变化的输入功率并需要恒定的输出功率。
AC-DC 转换器框图以及输入和输出功率图

图 1. AC-DC 转换器框图以及功率输入和功率输出图
(注:该图假设交流侧的功率因数为 1,因此转换器需要包括功率因数校正。在本文末尾,您可以看到交流功率的方程是如何推导的)
交流侧输入功率为\[p_{ac}(t)=P_{o} + P_{o}cos(2 omega t)\],直流侧输出功率为\[P_{o }\]。纹波功率部分(\[ P_{o}cos(2 \omega t)\] - 也在图中突出显示)需要通过转换器中的滤波器消除。实现该滤波器的常见方法是在输出端放置一个大电容器,如图 2 所示。该解决方案既简单又具有成本效益,但正如我们将看到的,滤波电容器存储的能量远多于实际所需的能量。过滤过程。

图 2. 输出端带有滤波电容器的 AC-DC 转换器
输出滤波器的大小(即所需的电容)由系统必须处理多少功率(\[P_{o}\])、交流电压的频率(\[\omega\]弧度每秒)、输出电压(\[V_{o}\])和允许的峰峰值电压纹波(\[V_{r}\])。将所有这些因素与电容相关的具体方程为:
\[C_{filt} = \frac{P_{o}}{\omega V_{o} V_{r}}\]
线路频率为 60 Hz、390V 时输出功率为 700W、纹波为 8V 的示例系统需要 595uF 的电容。如果您要测量该系统的输出电压,它会看起来像这样(请注意,为了说明目的,该图中的纹波被夸大了):
(AC-DC 转换器的)390V 输出电压示例,包括较大的峰峰值电压纹波。
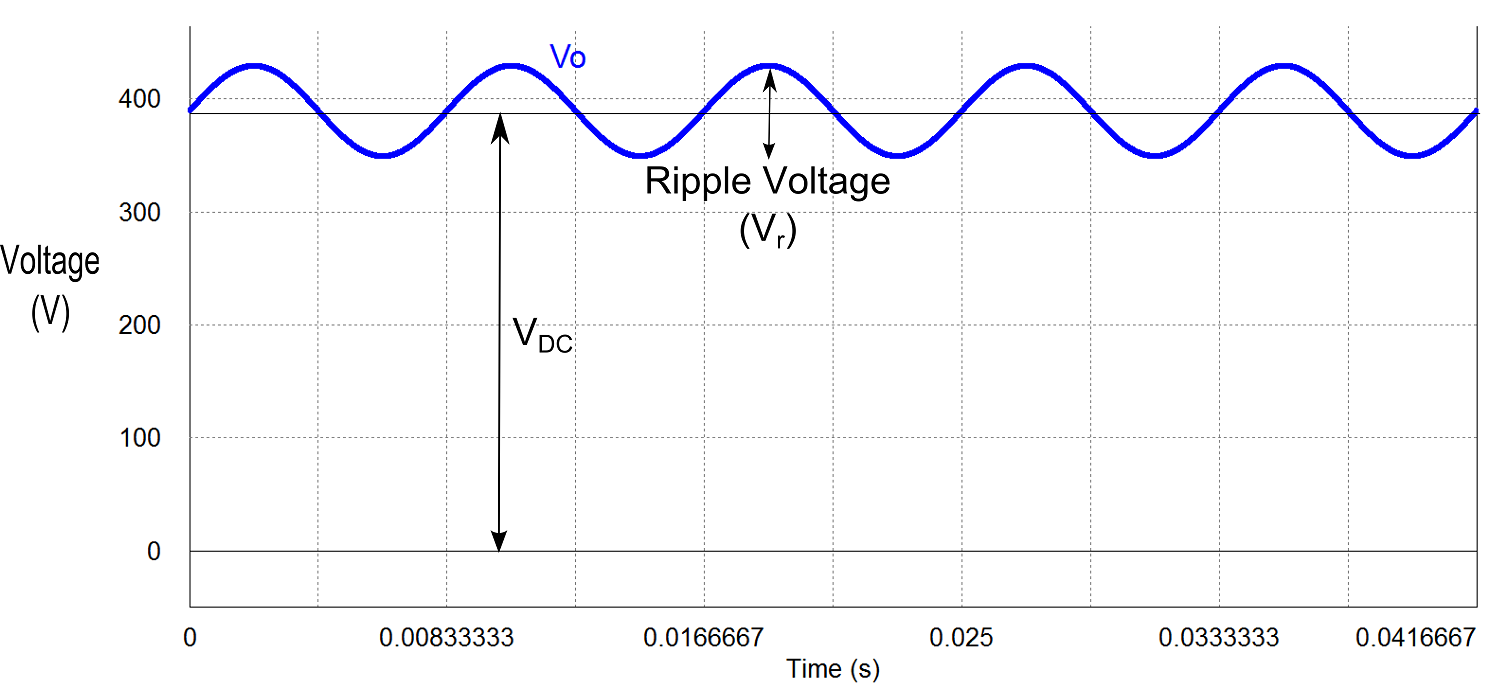
图 3. 具有纹波电压的输出电压示例
当提供的交流功率超过所需的直流功率时,电容器通过从交流电源吸收能量来完成其工作,并在提供的交流功率小于所需的直流功率时将能量返回到直流负载。问题是电容器中存储的大部分能量没有被使用。只有少量的功率流会产生实际上由电容器处理的电压纹波。不过,所有未使用的存储能量必须位于电容器中,以使电容器的电压达到输出所需的电压。这有点像一桶 10,000 升的水,龙头放置在距离顶部几厘米的地方:桶必须接近满才能将水排出,并且只能在水位低于水位时才能将水排出。龙头,那么你必须再次填充它。水龙头下方的所有水都无法使用。在滤波电容器中,所有存储的能量(除了电压纹波期间吸收和释放的少量能量)同样无法使用,因为您需要尽可能保持输出电压恒定。
如果您可以设计一个电路,可以控制电容器的电源纹波,以匹配转换器交流侧的电源纹波,并允许电压根据需要摆动,那么您将拥有一个有效的滤波器,可以显着降低双线频率纹波。该电路的部分是电容器不必存储任何额外的能量就可以工作。这种电容器的电压、电流和功率信号如下所示:
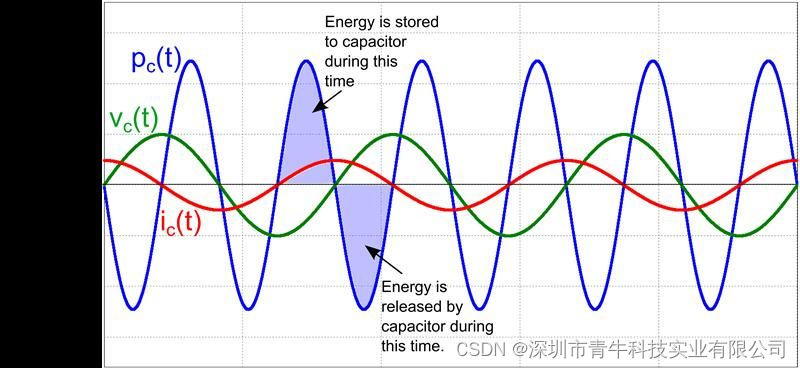
电容器的电压、电流和功率波形。
图 4. 假设滤波器电路的电压、电流和功率波形
这种电路的设计是可能的。创建此类电路的一种方法是添加与交流输入和直流输出分开的电源处理或纹波端口。该纹波端口需要存储组件(即电容器)和控制系统来控制端口的电源。如图 4 所示,当交流电源过高时,端口需要存储能量;而当交流电源过低时,则需要释放能量。纹波端口的框图如下图 5 所示。由于纹波端口与两者都是分开的输入和输出端口,两个端口都不对纹波端口的电压施加任何限制。正如您将看到的,通过允许电容器的峰值电压非常高,您可以将电容减小到任意低的值。
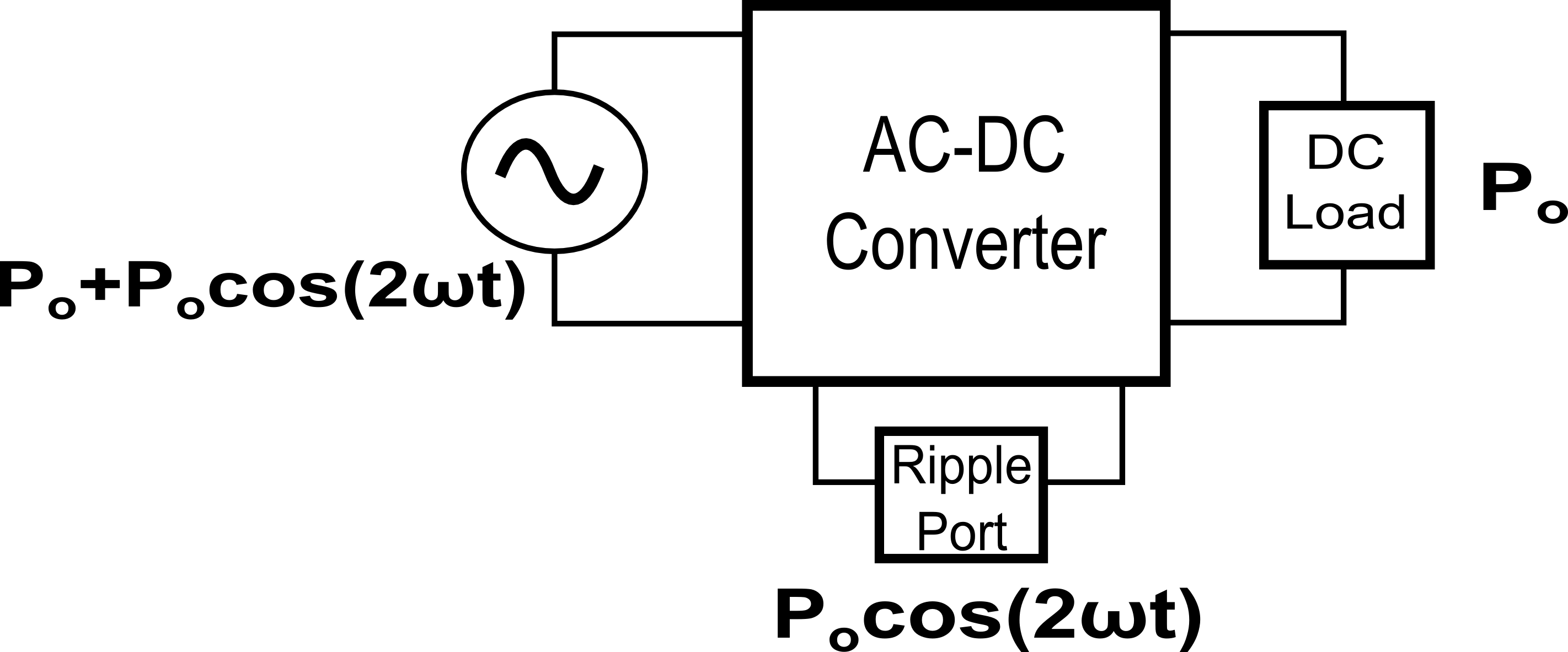
图 5. AC-DC 转换器中的纹波端口
学术文献中已经研究和描述了几种不同的纹波端口设计。此处讨论的Krein 等人的设计是一种因其简单性以及因其而在现实世界市场中显示出的潜力而脱颖而出的设计。
设计的总体思路是我们希望所有纹波功率 (\[P_{o}cos(2\omega t)\]) 来回流向纹波端口电容器。为了实现这一点,我们需要纹波功率方程来匹配电容器的功率方程。正弦交流电路中电容器的功率方程为
\[P_{c}(t)=v_{c}(t)i_{c}(t) = [ V_{c} cos(\omega t + \theta)] \times C\frac{dv_{c} {dt}\]
需要注意的是,\[\theta\] 表示系统交流侧电压与纹波端口电容器电压之间的相移。可以使用一些微积分和三角函数将上面的方程简化为
\[P_{c}(t) = -\omega CV_{c}^{2} \times sin(2\omega t+2\theta )\]
由于我们希望所有纹波功率都进入电容器,因此我们可以将电容器功率方程设置为等于纹波功率方程:
\[P_{o}cos(2\omega t) = \frac{-\omega CV_{c}^{2}}{2} \times sin(2\omega t+2\theta )\]
为了使该方程的两侧相等,幅度必须相同并且相移必须相同。
首先,让我们检查一下上式的幅度部分;因为它们必须相等,所以我们得到:
\[P_{o}= \frac{\omega CV_{c}^{2}}{2}\]
在此等式中您可以控制的两个元素是电容器和电容器的峰值电压 (\[V_{c}\])。让我们回到之前看到的 700W、390V 示例,概述如何确定纹波端口的峰值电压和电容。首先,您需要确定纹波端口的峰值电压。理论上,您可以选择任何您想要的电压,电压越高,电容可能越低,但出于安全原因,您可能希望选择小于或等于输出电压的电压。在这种情况下,我们将为纹波端口选择 300V,该电压比输出电压稍低,但足够高,我们应该可以很好地减少电容。接下来,您将计算过滤 700W 纹波功率所需的电容。
\[C=\frac{2P_{o}}{\omega V_{c}^2}\]
将 \[P_{o} = 700W\]、\[\omega=2\pi \times 60\] 和 \[V_{c}=300V\] 代入上述方程,得到 41uF。与原始设计中的电容器相比,这种新电容减少了 14.5 倍。如果我们使用\[V_{c}=390V\],电容甚至可以进一步减小到25uF。
我们还没有完成,我们已经确定了要使用的峰值电压和电容。接下来,我们需要确定电容器电压与交流输入电压相比的相移。要确定所需的相位差,请检查功率方程的相移部分,并将方程的电源纹波侧的相移设置为等于方程的电容器功率侧的相移:
\[-sin(2 \omega t + 2 \theta) = cos(2 \omega t)\]
通过一些简单的三角函数,这个方程可以解出\[\theta\]:
\[=cos(2 \omega t + 2 \theta + \frac{\pi}{2}) = cos(2 \omega t)\]
\[2 \omega t + 2 \theta + \frac{\pi}{2} = 2 \omega t\]
,如果求解 \[\theta\],它又是交流电源电压与纹波端口电压之间的相位差,则可以得到
\[\theta = -\frac{\pi}{4}\]
将幅度部分和相移部分放在一起,重要的是,如果将纹波端口的电压控制为
\[v_{c}(t)= \sqrt{\frac{2P_{o}}{\omega C}} sin(\omega t - \frac{\pi}{4})\]
那么纹波端口将吸收系统中的双线频率纹波功率。
在我们的示例 700W、390V 系统中,这意味着我们需要将纹波端口的电压(功率)控制为:
\[v_{c}(t)=300sin(\omega t - \frac{\pi}{4})\]
考虑到替代方案是简单地添加一个大电解电容器,这似乎需要大量工作。问题是电解电容器的预期寿命较短。通常,它们的预期寿命比电子系统中的任何其他组件都短,因此在需要数十年或更长预期寿命的系统中,电解电容器不是一个好的解决方案。薄膜电容器的寿命更长,但不幸的是,对于相同的电容,它比电解要贵得多。例如,快速搜索在线电子元件目录显示,一个600uF、600V的电解电容器大约为20美元,而相同额定值的薄膜电容器大约为200美元。使用这种纹波端口的系统将能够经济有效地使用薄膜电容器而不是电解电容器,因为电容要求会大大降低。当然,在使用这种系统之前,必须将纹波端口控制系统的成本与仅使用大(且昂贵)薄膜电容器的成本进行比较。
要注意的是,当您需要从直流电源生成交流电压时,可以将同类系统用于逆变器。对于内置微型逆变器的光伏板来说,电解电容器的可靠性问题确实成为一个问题,因为这些微型逆变器必须保修20-25年。该时间跨度比电解电容器在任何条件下的预期寿命都长得多。
这篇关于为什么电源滤波器中的电容器太大的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!