HDU2073 无限的路【水题】【递推】

本文主要是介绍HDU2073 无限的路【水题】【递推】，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

Problem Description
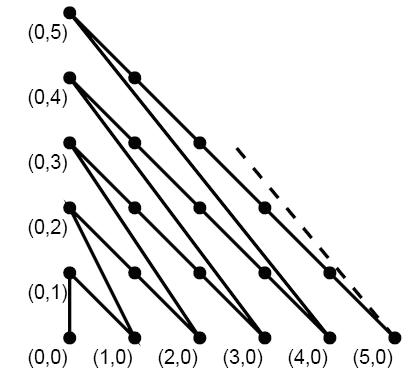
甜甜从小就喜欢画图画，最近他买了一支智能画笔，由于刚刚接触，所以甜甜只会用它来画直线，于是他就在平面直角坐标系中画出如下的图形：
甜甜的好朋友蜜蜜发现上面的图还是有点规则的，于是他问甜甜：在你画的图中，我给你两个点，请你算一算连接两点的折线长度（即沿折线走的路线长度）吧。
 
Input
第一个数是正整数N（≤100）。代表数据的组数。
每组数据由四个非负整数组成x1，y1，x2，y2；所有的数都不会大于100。
 
Output
对于每组数据，输出两点(x1,y1),(x2,y2)之间的折线距离。注意输出结果精确到小数点后3位。
 
Sample Input
5
0 0 0 1
0 0 1 0
2 3 3 1
99 99 9 9
5 5 5 5
 
Sample Output
1.000
2.414
10.646
54985.047
0.000
 
Author
Lily
 
Source

浙江工业大学网络选拔赛

题目大意：按照图上所示，给你两点坐标，求两点间的折线距离。

思路：利用递推。这里，模拟了从(0,0)点到(x,y)点折线路线递推的过程。

设i为横坐标，j为纵坐标。则路径为 先右下到纵坐标为0，再一步到达横

坐标为0的，纵坐标为原横坐标+1的位置。

所以直接模拟递推求。用ans[x][y]保存(0，0)点到(x，y)点的距离。最终

结果为：fabs(ans[x1][y1]-ans[x2][y2])。

#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cmath>
using namespace std;double ans[220][220];int main()
{for(int j = 1; j < 200; j++){for(int i = 0; i <= j; i++){if(i == 0)ans[i][j] = ans[j-1][i] + sqrt(1.0*j*j+1.0*(j-1)*(j-1));elseans[i][j-i] = ans[i-1][j-i+1] + sqrt(2.0);}}int N;int x1,y1,x2,y2;cin >> N;while(N--){cin >> x1 >> y1 >> x2 >> y2;printf("%.3lf\n",fabs(ans[x1][y1]-ans[x2][y2]));}return 0;
}

这篇关于HDU2073 无限的路【水题】【递推】的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---