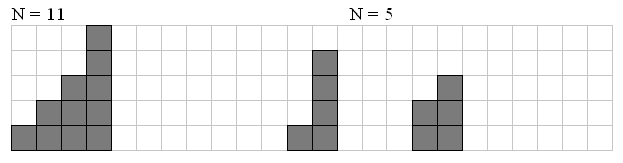本文主要是介绍URAL 1920 Titan Ruins: the Infinite Power of Magic,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
大意:
有一张N*N的网格,你每次可以走一步,每格只能走一次,有没有一种方法让走了L步后回到一个距原点1步远的格子?
没有输出Unsuitable device,否则输出Overwhelming power of magic并输出方案。
一开始用DFS 奇偶剪枝了还是TLE,
代码如下:
#include<iostream>
#include<cstring>
#include<cmath>
#define N 110
using namespace std;int n,t,end_i,end_j;
bool visited[N][N],flag,ans;
char map[N][N];
int run[10010][2];
int tem;
int a[4][2]={{-1,0},{1,0},{0,-1},{0,1}};void DFS(int i,int j,int c)
{
if(flag){ return ;}if(c>t) return ;if(i<=0||i>n||j<=0||j>n) {return ;}if(map[i][j]=='D'&&c==t) {flag=ans=true; return ;}int temp=abs(i-end_i)+abs(j-end_j);temp=t-temp-c; //t扣掉还要走的最短步temp 和 已经走过的 c 如果这些步还是奇数直接不满足if(temp&1) return ;//奇偶剪枝 奇数returnfor(int k=0;k<4;k++)if(!visited[i+a[k][0]][j+a[k][1]]) //开始进行各个方向的探索 记得回溯,取消之前走的状态{visited[i+a[k][0]][j+a[k][1]]=true;DFS(i+a[k][0],j+a[k][1],c+1);if(flag){cout<<i+a[k][0]<<" "<<j+a[k][1]<<endl;break;}visited[i+a[k][0]][j+a[k][1]]=false;}
}int main()
{int i,j;while(cin>>n>>t){if(t%2!=0||t>n*n){cout<<"Unsuitable device"<<endl;continue;}else cout<<"Overwhelming power of magic"<<endl;cout<<"1 1"<<endl;memset(visited,0,sizeof(visited));for(i=1;i<=n;i++){for(j=1;j<=n;j++){map[i][j]='.';}}end_i=2;end_j=1;map[2][1]='D';visited[1][1]=1;ans=flag=false;DFS(1,1,1);
// if(ans) cout<<"YES"<<endl;
// else cout<<"NO"<<endl;}return 0;
}后来是找规律做出来的,根据奇偶分类讨论一下;;
代码写的很烂。。
很多复用的没复用。。
#include<iostream>
#include<cstring>
#include<cmath>
#define N 110
using namespace std;int n,t,end_i,end_j;
bool visited[N][N],flag,ans;
char map[N][N];
int run[10010][2];
int tem;
int a[4][2]={{-1,0},{1,0},{0,-1},{0,1}};int main()
{int i;int xx,yy,kk;while(cin>>n>>t){if(t%2!=0||t>n*n){cout<<"Unsuitable device"<<endl;continue;}else cout<<"Overwhelming power of magic"<<endl;
// cout<<"1 1"<<endl;if(n%2==0){if(t<=2*n){for(i=1;i<=t/2;i++){cout<<1<<" "<<i<<endl;}for(i=t/2;i>0;i--){cout<<2<<" "<<i<<endl;}}else{kk=t-2*n;yy=kk/(2*(n-2));xx=kk%(2*(n-2));for(i=1;i<=n;i++){cout<<"1 "<<i<<endl;}if(xx!=0){int w2=n-2;for( i=2;i<=2+xx/2;i++){cout<<i<<" "<<n<<endl;}for( i=2+xx/2;i>=2;i--){cout<<i<<" "<<n-1<<endl;}while(yy--){for(i=2;i<=n;i++)cout<<i<<" "<<w2<<endl;for(i=n;i>=2;i--)cout<<i<<" "<<w2-1<<endl;w2-=2;}while(w2!=0){cout<<"2 "<<w2<<endl;cout<<"2 "<<w2-1<<endl;w2-=2;}}else{int wei;wei=n;while(yy--){for(i=2;i<=n;i++)cout<<i<<" "<<wei<<endl;for(i=n;i>=2;i--)cout<<i<<" "<<wei-1<<endl;wei-=2;}while(wei!=0){cout<<"2 "<<wei<<endl;cout<<"2 "<<wei-1<<endl;wei-=2;}}}}else{if(t<=2*n){for(i=1;i<=t/2;i++){cout<<1<<" "<<i<<endl;}for(i=t/2;i>0;i--){cout<<2<<" "<<i<<endl;}}else if(t<=2*n+2*(n-2)){int er=(t-(2*n))/2;for(i=1;i<=n;i++){cout<<1<<" "<<i<<endl;}for(i=n;i>=3;i--){cout<<2<<" "<<i<<endl;}for(i=2;i<=2+er;i++){cout<<i<<" "<<2<<endl;}for(i=er+2;i>=2;i--){cout<<i<<" "<<1<<endl;}}else if(t<=(n+n-1+3*(n-2))){int bb=(t-(2*n+2*(n-2)))/2;for(i=1;i<=n;i++){cout<<1<<" "<<i<<endl;}for(i=n;i>=3;i--){cout<<2<<" "<<i<<endl;}for(i=3;i<=n;i++){cout<<i<<" "<<3<<endl;}cout<<n<<" "<<2<<endl;int x=n,y=1;cout<<x<<" "<<y<<endl;x--;cout<<x<<" "<<y<<endl;while(1){if(x==2&&y==1){break;}if(bb>0&&y==1&&x%2==0){y=2;bb--;cout<<x<<" "<<y<<endl;}else if(y==2&&x%2==0){x--;cout<<x<<" "<<y<<endl;}else if(y==2&&x%2==1){y=1;cout<<x<<" "<<y<<endl;}else if(y==1&&x%2==1){x--;cout<<x<<" "<<y<<endl;}else if(bb<=0&&y==1&&x%2==0){x--;cout<<x<<" "<<y<<endl;}}}else{kk=t-(n+n-1+3*(n-2));yy=kk/(2*(n-2));xx=kk%(2*(n-2));for(i=1;i<=n;i++){cout<<"1 "<<i<<endl;}if(xx!=0){int w21=n-2;for( i=2;i<=2+xx/2;i++){cout<<i<<" "<<n<<endl;}for( i=2+xx/2;i>=2;i--){cout<<i<<" "<<n-1<<endl;}while(yy--){for(i=2;i<=n;i++)cout<<i<<" "<<w21<<endl;for(i=n;i>=2;i--)cout<<i<<" "<<w21-1<<endl;w21-=2;}while(w21!=3){cout<<"2 "<<w21<<endl;cout<<"2 "<<w21-1<<endl;w21-=2;}}else{int wei2;wei2=n;while(yy--){for(i=2;i<=n;i++)cout<<i<<" "<<wei2<<endl;for(i=n;i>=2;i--)cout<<i<<" "<<wei2-1<<endl;wei2-=2;}while(wei2!=3){cout<<"2 "<<wei2<<endl;cout<<"2 "<<wei2-1<<endl;wei2-=2;}}/***/for(i=2;i<=n;i++){cout<<i<<" "<<3<<endl;}cout<<n<<" "<<2<<endl;int x=n,y=1;cout<<x<<" "<<y<<endl;x--;cout<<x<<" "<<y<<endl;while(1){if(x==2&&y==1){break;}if(y==1&&x%2==0){y=2;cout<<x<<" "<<y<<endl;}else if(y==2&&x%2==0){x--;cout<<x<<" "<<y<<endl;}else if(y==2&&x%2==1){y=1;cout<<x<<" "<<y<<endl;}else if(y==1&&x%2==1){x--;cout<<x<<" "<<y<<endl;}}}}}return 0;
}
有的队也有用DFS过的T T
#include<iostream>
using namespace std;
int n,l,ans;
void dfs(int x,int y,int z){if(ans==l) return ;if(x>n||y>n) return ;if(z==0){printf("%d %d\n",x,y);ans+=2;dfs(x+1,y,0);printf("%d %d\n",x,y+1);if(n%2==x%2) dfs(x,3,1);}else if(z==1){printf("%d %d\n",x,y);ans+=2;dfs(x,y+1,1);printf("%d %d\n",x-1,y);if(x==3&&y%2==0) dfs(x-2,y,2);}else if(z==2){ans+=2;printf("%d %d\n",x,y);printf("%d %d\n",x,y-1);}
}
int main(){cin>>n>>l;if(l%2==1||n*n<l){printf("Unsuitable device\n");}else{printf("Overwhelming power of magic\n");printf("1 1\n");printf("2 1\n");ans=4;dfs(3,1,0);printf("2 2\n");if(ans!=n) dfs(2,3,1);printf("1 2\n");}return 0;
}
这篇关于URAL 1920 Titan Ruins: the Infinite Power of Magic的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!