2017ACM EC Final 补题题解

2024-06-13 04:18
文章标签 final 题解 补题 ec 2017acm

本文主要是介绍2017ACM EC Final 补题题解，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

M World Cup

傻逼签到不多说
代码

#include<bits/stdc++.h>
#include<iostream>
#include <stdio.h>
using namespace std;
const int maxn=100005;
const int base=131;
typedef long long ll;
#define pi acos(-1)
#define INF 0x3f3f3f3f
#define mod 998244353
const int inf=1<<30;
ll p[10];ll slove(int id)
{if(id >= 1 && id < 49)return p[1];if(id >= 49 && id < 57)return p[2];if(id >=57 && id < 61)return p[3];   if(id >=61 && id < 63)return p[4];return p[5];  
}
int main()
{int t,n;cin>>t;for(int j = 1; j <= t ;j++){for(int i = 1; i <= 5; i++)scanf("%lld",&p[i]);scanf("%d",&n);int id;ll ans = 0;for(int i =1;i <= n;i++){scanf("%d",&id);ans += slove(id);}ans *= 10000;printf("Case #%d: %lld\n",j,ans);}return 0;
}

A Chat Group

数学题
看一下n的数据范围，显然直接暴力不可能，看一下k的数据1e5，可以想到往k上面转化。
经典二项式的性质Cn0+Cn1+Cn2+……cnn=2^n，直接把加法转化为减法。注意由于算组合数有分母，需要用到逆元。
然后取余这个东西真的恶心，建议有结果的地方就取余，少了一个取余被卡了一小时还换了一种写法。
代码一（提前处理阶乘和全排列）

#include<bits/stdc++.h>
#include<iostream>
#include <stdio.h>
using namespace std;
const int maxn=100005;
const int base=131;
typedef long long ll;
#define pi acos(-1)
#define INF 0x3f3f3f3f
#define mod 1000000007
const int inf=1<<30;
ll A[maxn];
ll J[maxn];
ll ksm(ll a,ll b,ll m)
{ll ans = 1;while(b){if(b & 1) ans = (ans*a) % m ;a = (a * a) % m;b >>= 1;}return ans;
}void amn(ll m,ll n){A[0] = 1;for(ll i = 1,j = m;i<= n;i++){A[i] = A[i-1] * j;A[i] %= mod;j--; }
}void jiechen(ll k)
{J[0] = 1;for(int i  = 1 ; i <= k;i++ ){J[i] = (J[i-1] * i) % mod;}
}ll cmn(ll m ,ll n)
{return (A[n] * ksm(J[n],mod-2,mod)) %mod;
}int main()
{int t,n,k;cin>>t;jiechen(100000);for(int i = 1; i <= t; i++){cin>>n>>k;if( k > n){printf("Case #%d: 0\n",i);continue;}ll ans = ksm(2,n,mod);ll jishu = 0;amn(n,k);for(ll j = k-1 ; j >= 0; j--){jishu += cmn(n,j);jishu %= mod;}ans = (ans - jishu + mod) % mod;printf("Case #%d: %lld\n",i,ans);}return 0;
}

代码二 递推处理

#include<bits/stdc++.h>
#include<iostream>
#include <stdio.h>
using namespace std;
const int maxn=100005;
const int base=131;
typedef long long ll;
#define pi acos(-1)
#define INF 0x3f3f3f3f
#define mod 1000000007
const int inf=1<<30;
ll A[maxn];
ll J[maxn];
ll ksm(ll a,ll b,ll m)
{ll ans = 1;while(b){if(b & 1) ans = (ans*a) % m ;a = (a * a) % m;b >>= 1;}return ans;
}int main()
{int t,n,k;cin>>t;for(int i = 1; i <= t; i++){cin>>n>>k;if( k > n){printf("Case #%d: 0\n",i);continue;}ll ans = ksm(2,n,mod);ll jishu = 1;ll tmp = 1;for(ll j = 1,kk = n ; j <= k-1; j++){tmp = ((tmp * kk) % mod * ksm(j,mod-2,mod)) %mod;kk--;jishu += tmp;jishu %= mod;}ans = (ans - jishu + mod) % mod;printf("Case #%d: %lld\n",i,ans);}return 0;
}

KDowngrade

阅读理解题
可能是我英语不好吧，反正看了题解才知道题意。虽然它叫降级但是题意好像和降级并没有什么关系。
拿样例举例此时位于A-B（3-2），这一天羊神缺席，B舍弃，A转化为经验值3点，从零开始升级就是2-1，继续第二天，1舍弃，2转化为经验值2点，从零开始升级就是1-2。
题意知道了就是纯模拟了。
代码：（二分查找）

#include<bits/stdc++.h>
#include<iostream>
#include <stdio.h>
using namespace std;
const int maxn=100005;
const int base=131;
typedef long long ll;
#define pi acos(-1)
#define INF 0x3f3f3f3f
#define mod 1000000007
const int inf=1<<30;
ll l[maxn];
ll up[maxn];ll find(ll x)
{ll l = 1;ll r = x;while(l <= r){ll m = (l + r) / 2;if(up[m] < x && up[m+1] >= x)return m;else if(x <= up[m])r = m-1;elsel = m+1;}return 0;
}int main()
{int t,a,b,n;cin>>t;for(int c = 1; c <= t ; c++ ){memset(up,0,sizeof(up));cin>>a>>b>>n;for(int i = 1; i <= a; i++){scanf("%lld",&l[i]);up[i] = up[i-1] + l[i];}ll x,y,lx;x = a;y = b;while(n--){if(x == lx)break;lx = x;x = find(x) + 1;y = lx - up[x-1];}printf("Case #%d: %lld-%lld\n",c,x,y); }return 0;
}

普通：

#include<bits/stdc++.h>
#include<iostream>
#include <stdio.h>
using namespace std;
const int maxn=100005;
const int base=131;
typedef long long ll;
#define pi acos(-1)
#define INF 0x3f3f3f3f
#define mod 1000000007
const int inf=1<<30;
ll l[maxn];int main()
{int t,a,b,n;cin>>t;for(int c = 1; c <= t ; c++ ){cin>>a>>b>>n;for(int i = 1; i <= a; i++)scanf("%lld",&l[i]);ll x,y,lx;x = a;y = b;while(n--){if(x == lx)break;lx = x;y = x;x = 1;for(int i = 1; i <= x;i++){if(y > l[i]){y -= l[i];x++;}elsebreak;}if(x == 1 && y == 1)break;}printf("Case #%d: %lld-%lld\n",c,x,y); }return 0;
}

CTraffic Light

又是一个阅读理解，最糟糕的情况下最短时间就是等最长的红灯，其他都是绿灯。

#include<bits/stdc++.h>
#include<iostream>
#include <stdio.h>
using namespace std;
const int maxn=100005;
const int base=131;
typedef long long ll;
#define pi acos(-1)
#define INF 0x3f3f3f3f
#define mod 1000000007
const int inf=1<<30;
ll s[maxn];
ll a[maxn],b[maxn];int main()
{int t,n;cin>>t;for(int c =1 ;c <= t ;c++){cin>>n;double ans = 0.0;for(int i = 1;i <= n+1; i++){scanf("%lld",&s[i]);ans += s[i];}for(int i = 1;i <= n; i++ )scanf("%lld %lld",&a[i],&b[i]);sort(b+1, b+1+n);ans += b[n];printf("Case #%d: %.8lf\n",c,ans); }return 0;
}

B. Scapegoat

题意：每个人都对应一个麻烦，n个人可以对应同一个麻烦，找最小方差。

思路：一个贪心的思维，平均值一定，那么先把所有的麻烦分出去，这时候有一个方差，然后加人，每个麻烦下面都可以加，然后计算方差的变化，每次往下降最多的那个麻烦下加人。
平均数不会变，每个麻烦分的人加一个人后的方差改变为：
c n t ∗ ( n u m / c n t − a v g ) 2 − ( c n t + 1 ) ∗ ( n u m / ( c n t + 1 ) − a v g ) 2 cnt * (num / cnt - avg)^2 - (cnt + 1) * (num / (cnt + 1) - avg)^2 cnt∗(num/cnt−avg)2−(cnt+1)∗(num/(cnt+1)−avg)2

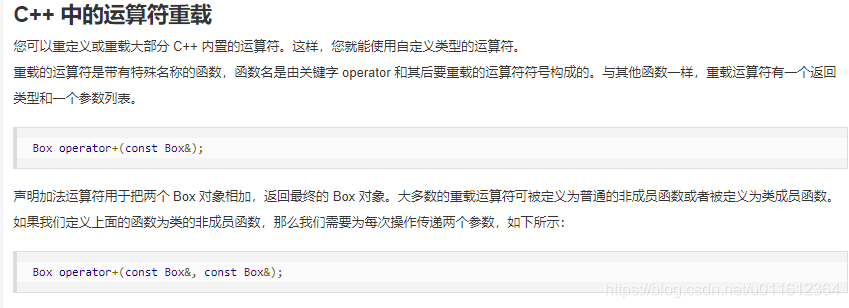
不会写重载比较操作符函数，见下图
在这里插入图片描述
代码

- #include<bits/stdc++.h>#include<iostream>#include <stdio.h> using namespace std; const int maxn=200005; const int base=131; typedef long long ll;#define pi acos(-1)#define INF 0x3f3f3f3f#define mod 998244353 const int inf=1<<30; double a[maxn]; double avg,sum;struct node {double num,cnt;double val;bool operator < (const node& b) const {return val < b.val;} };double cal(node x) {return  x.cnt * (x.num / x.cnt - avg) * (x.num / x.cnt - avg) - (x.cnt + 1) * (x.num / (x.cnt + 1) - avg) * (x.num / (x.cnt + 1) -avg);//增加一个后方差的减小量  }int main() {int t,n,m;cin>>t;for (int c = 1; c <= t; c++){double ans = 0.0;sum = 0.0;cin>>n>>m;for(int i = 1 ;i <= n; i++){scanf("%lf",&a[i]);sum += a[i];}avg = sum / m;priority_queue<node> q;for(int i = 1 ;i <= n; i++){node now;now.num = a[i];now.cnt = 1;now.val = cal(now);q.push(now);} for(int i = 1 ;i <= m - n; i++){node now = q.top();q.pop();now.cnt++;now.val = cal(now);q.push(now);}while(!q.empty()){node now = q.top();q.pop();ans += now.cnt * (now.num / now.cnt - avg) * (now.num / now.cnt - avg);}//cout<<ans<<endl;printf("Case #%d: %.12lf\n",c,ans/m);}return 0; }

以上是铜牌题

J. Straight Master

题意：给出一副扑克牌每张牌的张数，问能否以3张或5张顺子的形式将扑克牌打出去。
知识点：
思路：差分，然后看差分数组 b b b最后能否变为全为0的差分数组。
差分后对 [ l , r ] [l,r] [l,r]操作，就相当于减小差分数组中 b [ l ] b[l] b[l]，增加 b [ r + 1 ] b[r+1] b[r+1]。

从差分组数组第一项开始，对于大于0的项 i i i，找到最接近的小于0的项 j j j，如果 i i i和 j j j距离大于3就对这个范围操作，把此时的 b [ i ] b[i] b[i]变成 m i n ( 0 , b [ i ] + b [ j ] ) min(0,b[i] + b[j]) min(0,b[i]+b[j])，之所以这里不管距离大于5的限制，是因为完全可以通过多次连续合法的操作，完成距离大于5的操作。

可以预处理每一次的差分组数组值小于0的项的位置，节约时间。

最后如果全都变为0，就是yes，反之为no

#include<bits/stdc++.h>
#include<iostream>
#include <stdio.h>
using namespace std;
const int maxn=200005;
const int base=131;
typedef long long ll;
#define pi acos(-1)
#define INF 0x3f3f3f3f
#define mod 998244353
const int inf=1<<30;
int a[maxn];
int b[maxn];
vector<int> pos;
int main()
{//freopen("data.in","r",stdin);//freopen("1.out","w",stdout);int t,n,m;cin>>t;for(int c = 1 ; c <= t;c++ ){pos.clear();cin>>n;for(int i = 1 ; i <= n;i++){scanf("%d",&a[i]);b[i] = a[i] - a[i-1];if(b[i] < 0)pos.push_back(i);}b[n+1] = 0 - a[n];if(b[n+1] < 0)pos.push_back(n+1);int j = 0;int f = 1;for(int i = 1;i <= n+1;){if(b[i] > 0){if((pos[j] - i) >= 3 ){if(b[i] + b[pos[j]] > 0){b[i] = b[i] + b[pos[j]];b[pos[j]] = 0;j++;continue;}else{b[pos[j]] = b[i] + b[pos[j]];b[i] = 0;if(b[pos[j]] == 0)j++;}}else{f = 0;break;}}if(j >= pos.size() && b[i] != 0){f = 0;break;}i++;}if(f)printf("Case #%d: Yes\n",c);elseprintf("Case #%d: No\n",c);}return 0;
}

这篇关于2017ACM EC Final 补题题解的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/1056257。

相关文章

C++ | Leetcode C++题解之第393题UTF-8编码验证

C++ | Leetcode C++题解之第393题UTF-8编码验证

题目： 题解： class Solution {public:static const int MASK1 = 1 << 7;static const int MASK2 = (1 << 7) + (1 << 6);bool isValid(int num) {return (num & MASK2) == MASK1;}int getBytes(int num) {if ((num &
阅读更多...
C语言 | Leetcode C语言题解之第393题UTF-8编码验证

C语言 | Leetcode C语言题解之第393题UTF-8编码验证

题目： 题解： static const int MASK1 = 1 << 7;static const int MASK2 = (1 << 7) + (1 << 6);bool isValid(int num) {return (num & MASK2) == MASK1;}int getBytes(int num) {if ((num & MASK1) == 0) {return
阅读更多...
C - Word Ladder题解

C - Word Ladder题解

C - Word Ladder 题解 解题思路： 先输入两个字符串S 和t 然后在S和T中寻找有多少个字符不同的个数（也就是需要变换多少次） 开始替换时： tips: 字符串下标以0开始 我们定义两个变量a和b，用于记录当前遍历到的字符 首先是判断：如果这时a已经==b了，那么就跳过，不用管； 如果a大于b的话：那么我们就让s中的第i项替换成b，接着就直接输出S就行了。 这样
阅读更多...
【秋招笔试】9.07米哈游秋招改编题-三语言题解

【秋招笔试】9.07米哈游秋招改编题-三语言题解

🍭 大家好这里是 春秋招笔试突围，一起备战大厂笔试 💻 ACM金牌团队🏅️ | 多次AK大厂笔试 ｜ 大厂实习经历 ✨ 本系列打算持续跟新 春秋招笔试题 👏 感谢大家的订阅➕ 和 喜欢💗 和 手里的小花花🌸 ✨ 笔试合集传送们 -> 🧷春秋招笔试合集 🍒 本专栏已收集 100+ 套笔试题，笔试真题 会在第一时间跟新 🍄 题面描述等均已改编，如果和你笔试题看到的题面描述
阅读更多...
LeetCode 第414场周赛个人题解

LeetCode 第414场周赛个人题解

目录 Q1. 将日期转换为二进制表示 原题链接 思路分析 AC代码 Q2. 范围内整数的最大得分 原题链接 思路分析 AC代码 Q3. 到达数组末尾的最大得分 原题链接 思路分析 AC代码 Q4. 吃掉所有兵需要的最多移动次数 原题链接 思路分析 AC代码 Q1. 将日期转换为二进制表示 原题链接 Q1. 将日期转换为二进制表示 思路分析
阅读更多...
牛客小白月赛100部分题解

牛客小白月赛100部分题解

比赛地址：牛客小白月赛100_ACM/NOI/CSP/CCPC/ICPC算法编程高难度练习赛_牛客竞赛OJ A.ACM中的A题 #include<bits/stdc++.h>using namespace std;#define ll long long#define ull = unsigned long longvoid solve() {ll a,b,c;cin>>a>>b>
阅读更多...
P2858 [USACO06FEB] Treats for the Cows G/S 题解

P2858 [USACO06FEB] Treats for the Cows G/S 题解

P2858 题意 给一个数组。每天把最左或者最右的东西卖掉，第 i i i个东西，第 d a y day day天卖出的价格是 a [ i ] ∗ d a y a[i]*day a[i]∗day。 记忆化搜索 void dfs(int l,int r,int day,ll sum){if(v[l][r]>=sum)return;v[l][r]=sum;if(l>r)//这就是dp答案{
阅读更多...
【C++题解】1272. 郭远摘苹果

【C++题解】1272. 郭远摘苹果

欢迎关注本专栏《C++从零基础到信奥赛入门级（CSP-J）》 问题：1272. 郭远摘苹果 类型：二维数组 题目描述： 郭远有一天走到了一片苹果林，里面每颗树上都结有不同数目的苹果，郭远身上只能拿同一棵树上的苹果，他每到一棵果树前都会把自己身上的苹果扔掉并摘下他所在树上的苹果并带走（假设郭远会走过每一棵苹果树），问在郭远摘苹果的整个过程中，他身上携带的最多苹果数与最小苹果数的差是多少？
阅读更多...
【最新华为OD机试E卷-支持在线评测】机器人活动区域(100分)多语言题解-(Python/C/JavaScript/Java/Cpp)

【最新华为OD机试E卷-支持在线评测】机器人活动区域(100分)多语言题解-(Python/C/JavaScript/Java/Cpp)

🍭 大家好这里是春秋招笔试突围 ，一枚热爱算法的程序员 ✨ 本系列打算持续跟新华为OD-E/D卷的三语言AC题解 💻 ACM金牌🏅️团队| 多次AK大厂笔试 ｜ 编程一对一辅导 👏 感谢大家的订阅➕ 和 喜欢💗 🍿 最新华为OD机试D卷目录，全、新、准，题目覆盖率达 95% 以上，支持题目在线评测，专栏文章质量平均 94 分 最新华为OD机试目录: https://blog.
阅读更多...
2023 CCPC（秦皇岛）现场（第二届环球杯.第 2 阶段：秦皇岛）部分题解

2023 CCPC（秦皇岛）现场（第二届环球杯.第 2 阶段：秦皇岛）部分题解

所有题目链接：Dashboard - The 2023 CCPC (Qinhuangdao) Onsite (The 2nd Universal Cup. Stage 9: Qinhuangdao) - Codeforces 中文题面： contest-37054-zh.pdf (codeforces.com) G. Path 链接： Problem - G - Codeforces
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2