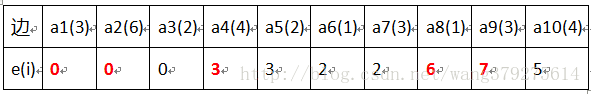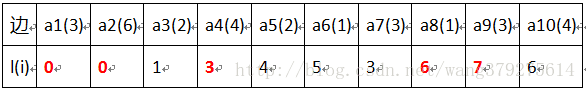本文主要是介绍教你轻松计算AOE网关键路径,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
转:教你轻松计算AOE网关键路径
认识AOE网
有向图中,用顶点表示活动,用有向边表示活动之间开始的先后顺序,则称这种有向图为AOV网络;AOV网络可以反应任务完成的先后顺序(拓扑排序)。
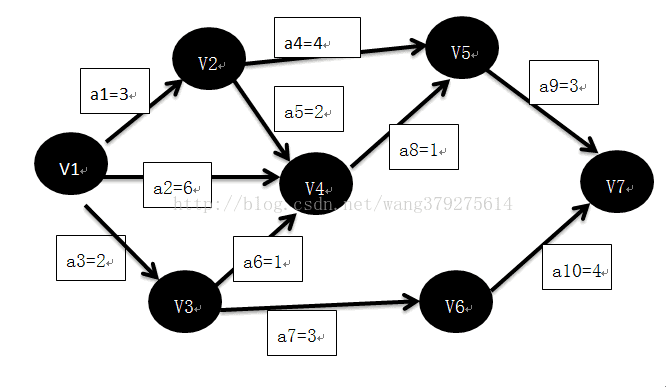
在AOV网的边上加上权值表示完成该活动所需的时间,则称这样的AOV网为AOE网,如下图:
图中,顶点表示事件(能被触发,两特征属性:最早发生时间Ve(j);最晚发生时间Vl(j)),边表示活动(能被开始,两特征属性:最早开始时间e(i);最晚开始时间l(i)),权表示活动持续时间,通常用AOE网来估算工程完成的时间
两条原则:
Ø 只有某顶点所代表的事件发生后,从该顶点出发的各活动才能开始
Ø 只有进入某顶点的各活动都结束,该顶点所代表的事件才能发生
计算关键路径
首先,在AOE网中,从始点到终点具有最大路径长度(该路径上的各个活动所持续的时间之和)的路径为关键路径。
计算关键路径,只需求出上面的四个特征属性,然后取e(i)=l(i)的边即为关键路径上的边(关键路径可能不止一条)。
先来看看四个特征属性的含义:
Ø Ve(j):是指从始点开始到顶点Vk的最大路径长度
计算技巧:
(1)从前向后,取大值:直接前驱结点的Ve(j)+到达边(指向顶点的边)的权值,有多个值的取较大者
(2)首结点Ve(j)已知,为0
如上图各顶点(事件)的Ve(j): (从V1开始)
V1 :天然是0
V2:a1边 3
V3:a3边 2
V4:分三种情况①a1 + a5 = 5 ②a2 = 6 ③a3 + a6 = 3 取最大者
V5:........
V6:........
Ø Vl(j):在不推迟整个工期的前提下,事件vk允许的最晚发生时间
计算技巧:
(1)从后向前,取小值:直接后继结点的Vl(j) –发出边(从顶点发出的边)的权值,有多个值的取较小者;
(2)终结点Vl(j)已知,等于它的Ve(j))
如上图各顶点(事件)的Vl(j): (从V7开始,它的最早、最晚发生时间相同,都为10):
V7:天然等于最大路径长度 10
V6:由V7 = 10 有 10 - a10 = 6
V5:由V7 = 10 有10 - a9 = 7
V4:由V5 = 7 有7 - a8 = 6
V3:有两个后继 V4和V6,所以分两种情况①V4 - a6 = 5 ②V6 - a7 = 3 取最小者, 所以V3 = 3
V2:........
Ø e(i): 若活动ai由弧<vk,vj>表示,则活动ai的最早开始时间应该等于事件vk的最早发生时间。因而,有:e[i]=ve[k];(即:边(活动)的最早开始时间等于,它的发出顶点的最早发生时间)
如上图各边(活动)的e(i):
活动发生最早时间看的是活动边的前驱节点
a1 a2 a3 前驱节点都是V1 然后从第一个图中,即最早发生事件中取值 a1= 0 a2 = 0 a3 = 0
a4 前驱节点是V2 所以有a4 = 3
a5.....
a6......
Ø l(i): 若活动ai由弧<vk,vj>表示,则ai的最晚开始时间要保证事件vj的最迟发生时间不拖后。 因而有:l[i]=vl[j]-len<vk,vj>1(为边(活动)的到达顶点的最晚发生时间减去边的权值)
如上图各边(活动)的l(i):
活动的最晚发生时间 等于事件的最晚发生时间(第二个图)减去活动边
即活动边的后继,去图2中找,然后减去活动边
a4活动边后继是V5 由最晚发生事件得 V5 - a4 = 7 - 4 = 3
至此已介绍完了四个特征属性的求法,也求出了上图中边的e(i)和l(i),取出e(i)=l(i)的边为a1、a2、a4、a8、a9,即为关键路径上的边,所以关键路径有两条:a1 a4 a9和 a2 a8 a9
==========================================================================
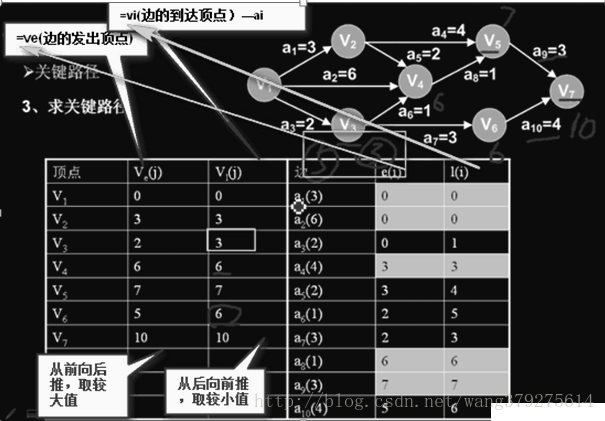
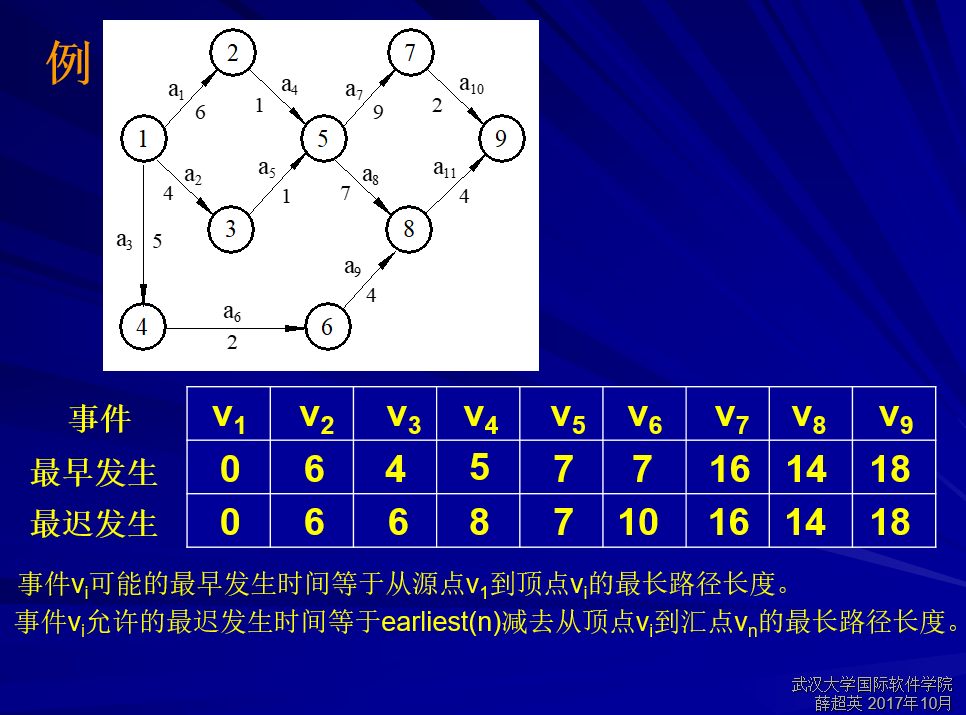
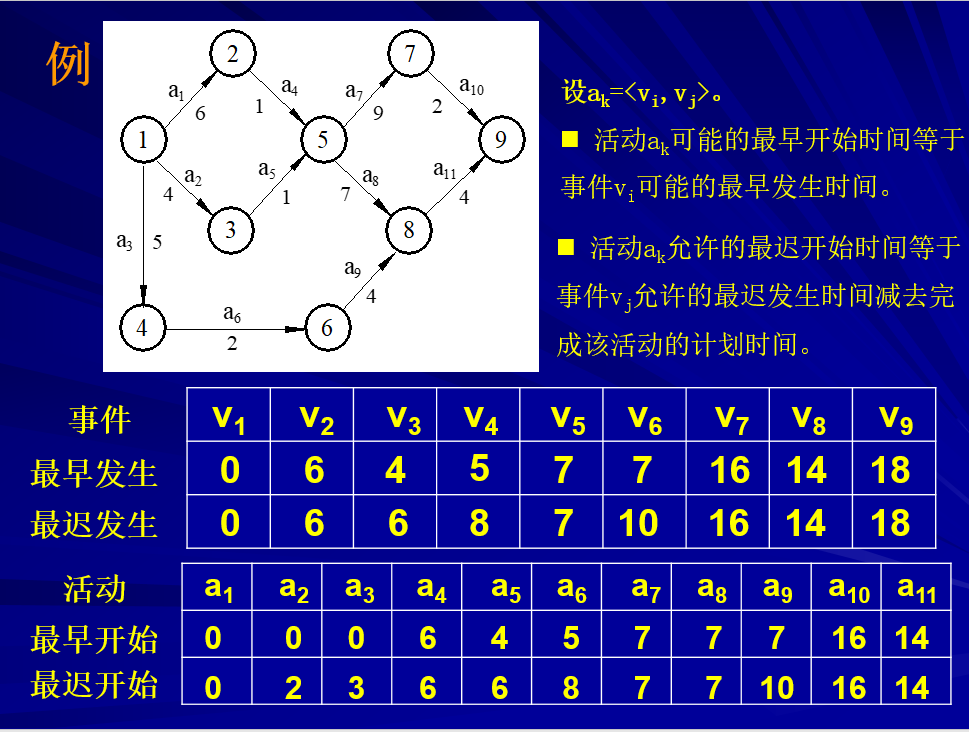
第二个例子对比一下
(最早发生,从前往后算;最迟发生,从后往前算。)
总结
求关键路径,只需理解顶点(事件)和边(活动)各自的两个特征属性以及求法即可:
Ø 先根据首结点的Ve(j)=0由前向后计算各顶点的最早发生时间
Ø 再根据终结点的Vl(j)等于它的Ve(j)由后向前依次求解各顶点的最晚发生时间
Ø 根据边的e(i)等于它的发出顶点的Ve(j)计算各边的最早开始时间(最早开始,对应最早发生)
Ø 根据边的l(i)等于它的到达顶点的Vl(j)减去边的权值计算各边的最晚开始时间(最晚开始,对应最晚发生)
这篇关于教你轻松计算AOE网关键路径的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!