本文主要是介绍模板显式、隐式实例化和(偏)特化、具体化的详细分析,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
最近看了<The C++ Programing Language>看到了模板的特化,突然想起来<C++ Primer>上说的显式具体化、隐式具体化、特化、偏特化、具体化等概念弄得头晕脑胀,我在网上了找了好多帖子,才把概念给理清楚。
看着这么多叫法,其实就是三种:
- 显示实例化
- 隐式实例化
- 特化(=具体化)、偏特化
一、实例化
1.显示、隐式实例化
什么是实例化:一个通过使用具体值替换模板参数,从模板产生的普通类,函数或者成员函数的过程。
显示实例化:通过名字可见,就是清楚的表明你要实例化的类型
隐式实例化:通过编译器自己推测判断要实例化的类型。
比如一个模板:
template<class T> //函数模板实现
void swap(T &a, T &b)
{T temp;temp = a;a = b;b = temp;
}
a. 显示实例化
template void swap(); // 无须给该函数重新编写函数体,这只是个声明
为什么要显示实例化?
主要是提高效率,当显式实例化模板时,在使用模板之前,编译器根据显式实例化指定的类型生成模板实例,这样就相当于本程序里面有个一
void swap(int &a, int &b)
{int temp;temp = a;a = b;b = temp;
}
这样的话,每次需要调用 swap(a,b)的时候每次都重新生成该类型的代码,可以节省空间,也能提高效率。这就是为什么要是显式的实例化的原因。
b. 隐式实例化
隐式实例化指的是:在使用模板之前,编译器不生成模板的声明和定义实例。只有当使用模板时,编译器才根据模板定义生成相应类型的实例。
int i=0, j=1;
swap(i, j); //编译器根据参数i,j的类型隐式地生成swap(int &a, int &b)的函数定义。
隐式实例化就是程序员为了省事,把类型省略让编译器判断,这是一个偷懒的表现吧。
二、特化
1. 特化(=具体化)
然而通常又有一些特殊的情况,不能直接使用泛型模板展开实现,这时就需要针对某个特殊的类型或者是某一类特殊的类型,而实现一个特例模板————即模板特化当T如果为 一个 struct类型的,它的交换就无法进行,所以我们针对这种特殊的情形,我们专门写了一个函数,只有当T为 这种struct类型时候,才会调用这个特化的函数
//对函数
#define MAXNAME 128
struct job
{
char name[MAXNAME]:
int salary;
};template<class T>
void swap(T &a, T &b )
{T temp;temp = a;a = b;b = temp;
};template void swap<int>(int &a, int & b); //显式实例化,只需声明template<> void swap<job>(job &a, job &b) //显式具体化(上面已经讲过,注意与实例化区分开,必须有定义)
{int salary:salary = a.salary:a.salary = b.salary;b.salary = salary;
};//explicite specialization.//对类模板:
template <class T>
class Arrary
{
private:T* ar;int l;
...
};//template class declaration.template class Array<int>; //explicit instantiation. 显式实例化template<> class Array<job>
{
private:job* ar;int l;
};//expicit specialization. 显式具体化,类定义体可以不同于类模板Array
2. 偏特化
模板的偏特化是指需要根据模板的部分参数进行特化。
a. 类模板的偏特化
-
参数
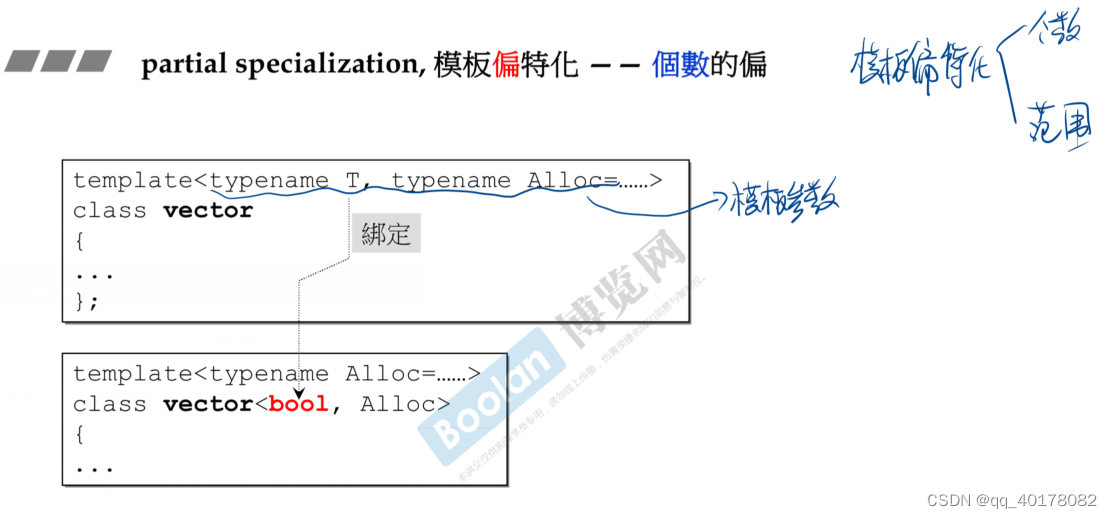
-
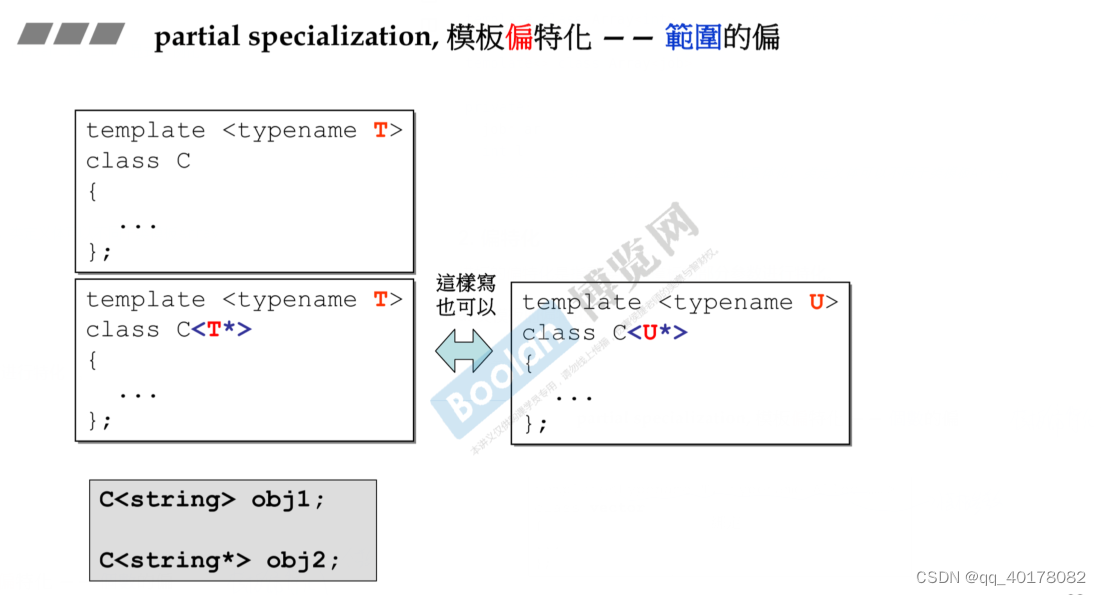
范围
-
b. 函数模板的偏特化
网上看到有人说:从严格意义上讲,函数模板并不支持偏特化(我对这个不是很理解),但由于可以对函数进行重载,所以可以达到类似于类模板偏特化的效果。
比如:
a) template void f(T);
根据重载规则,对a)进行重载
b) template < class T> void f(T*);
如果将a)称为基模板,那么b)称为对基模板a)的重载,而非对a)的偏特化。
这里我就不深入的剖析偏特化了。
三、模板的匹配顺序
1. 类模板的匹配规则
例如:
template class vector{//…//}; // (a) 普通型
template class vector ; // (b) 的显式实例化
template class vector<T*>{//…//}; // © 对指针类型特化
template <> class vector <void*>{//…//}; // (d) 对void进行特化
每个类型都可以用作普通型(a)的参数,但只有指针类型才能用作(b)的参数,而只有void才能作为©的参数
所以,当一个调用一个模板类,首先,找显式实例化的,如果不匹配;接着,找特化的,然后,找偏特化的,最后,根据模板隐式实例化
2.函数模板的匹配规则
例如:
void swap(int &a, int &b){} // 普通的函数
template<> swap(int &a, int &b){} // 特化的模板函数
template void swap(int &a, int &b); // 显式实例化,这个只用声明就行
template void swap(T &a, T &b){} // 模板
以上书写的顺序就是模板的调用顺序。
这篇关于模板显式、隐式实例化和(偏)特化、具体化的详细分析的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





