AVL树 ---（C++）

2024-06-10 12:12
文章标签 c++ avl

本文主要是介绍AVL树 ---（C++），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

        本篇讲全面的讲解 AVL 树的插入，旋转以及验证 AVL 树的性能（本篇未实现删除代码）。至于为什么会有 AVL 树，这是因为简单的二叉搜索树并不能直接的保证搜索的效率，因为当我们在二叉搜索树中插入一段有序的序列的时候，二叉搜索树就会退化为单枝树，这个时候进行搜索的时候，时间复杂度就变为了 O(n^2)，如下：

        但是通过 AVL 树的旋转就可以很好的解决这个问题，使树近似等于完全二叉树或者满二叉树。

AVL 树代码

        先给出代码，接着在下文中给出解释：

#pragma once
#include <iostream>
#include <assert.h>using namespace std;template <class K, class V>
struct AVLTreeNode {AVLTreeNode<K, V>* _left;AVLTreeNode<K, V>* _right;AVLTreeNode<K, V>* _parent;pair<K, V> _kv;int _balanceFactor;AVLTreeNode(const pair<K, V>& kv): _left(nullptr), _right(nullptr), _parent(nullptr), _kv(kv), _balanceFactor(0){}
};template <class K, class V>
class AVLTree {
public:typedef AVLTreeNode<K, V> Node;Node* find(const K& key) {Node* cur = _root;while (cur) {if (cur->_kv.first < key)cur = cur->_right;else if (cur->_kv.first > key)cur = cur->_left;elsereturn cur;}return nullptr;}// 插入删除查找遍历bool insert(const pair<K, V>& kv) {if (_root == nullptr) {_root = new Node(kv);return true;}// 开始查找Node* parent = nullptr;Node* cur = _root;while (cur) {if (cur->_kv.first < kv.first)parent = cur, cur = cur->_right;else if (cur->_kv.first > kv.first)parent = cur, cur = cur->_left;elsereturn false;}// cur == nullptrcur = new Node(kv);//if (parent->_left == cur)//	parent->_left = cur;//else//	parent->_right = cur;if (parent->_kv.first > kv.first)parent->_left = cur;elseparent->_right = cur;cur->_parent = parent;// 需要更新平衡因子// 如果是在父亲的左边，父亲的平衡因子减一、右边加一if (parent->_left == cur)parent->_balanceFactor--;elseparent->_balanceFactor++;// 查看爷爷结点是否需要更新while (parent) {if (parent->_balanceFactor == 0) {break;}else if (parent->_balanceFactor == 1 || parent->_balanceFactor == -1) {if (parent == _root)break;// 现在的parent就不可能等于nullparent = parent->_parent;cur = cur->_parent;if (parent->_left == cur)parent->_balanceFactor--;elseparent->_balanceFactor++;}else if(parent->_balanceFactor == 2 || parent->_balanceFactor == -2) {if (parent->_balanceFactor == 2 && cur->_balanceFactor == 1)RotateLeft(parent);else if (parent->_balanceFactor == -2 && cur->_balanceFactor == -1)RotateRight(parent);else if (parent->_balanceFactor == -2 && cur->_balanceFactor == 1)RotateLeftRight(parent);else if (parent->_balanceFactor == 2 && cur->_balanceFactor == -1)RotateRightLeft(parent);elseassert(false);break;}else {assert(false);}}return true;}void RotateRight(Node* parent) {Node* subL = parent->_left;Node* subLR = subL->_right;// 将左孩子的右节点链接到原父亲结点if (subLR) subLR->_parent = parent;parent->_left = subLR;Node* ppNode = parent->_parent;// 将左孩子变为原父亲结点的父亲subL->_right = parent;parent->_parent = subL;// 将爷爷结点重新链接if (ppNode == nullptr) {_root = subL;_root->_parent = nullptr;}else {if (ppNode->_left == parent)ppNode->_left = subL;elseppNode->_right = subL;subL->_parent = ppNode;}subL->_balanceFactor = parent->_balanceFactor = 0;}void RotateLeft(Node* parent) {Node* subR = parent->_right;Node* subRL = subR->_left;Node* ppNode = parent->_parent;parent->_right = subRL;if (subRL) subRL->_parent = parent;subR->_left = parent;parent->_parent = subR;if (ppNode == nullptr) {_root = subR;_root->_parent = nullptr;}else {if (ppNode->_left == parent)ppNode->_left = subR;elseppNode->_right = subR;subR->_parent = ppNode;}subR->_balanceFactor = parent->_balanceFactor = 0;}void RotateRightLeft(Node* parent) {Node* subR = parent->_right;Node* subRL = subR->_left;int balanceFactor = subRL->_balanceFactor;RotateRight(subR);RotateLeft(parent);// 更新平衡因子subRL->_balanceFactor = 0;if (balanceFactor == -1) {parent->_balanceFactor = 0;subR->_balanceFactor = 1;}else if (balanceFactor == 1) {parent->_balanceFactor = -1;subR->_balanceFactor = 0;}else if (balanceFactor == 0) {parent->_balanceFactor = 0;subR->_balanceFactor = 0;}else {assert(false);}}void RotateLeftRight(Node* parent) {Node* subL = parent->_left;Node* subLR = subL->_right;int balanceFactor = subLR->_balanceFactor;// 先左旋后右旋RotateLeft(subL);RotateRight(parent);subLR->_balanceFactor = 0;if (balanceFactor == -1) {subL->_balanceFactor = 0;parent->_balanceFactor = 1;}else if (balanceFactor == 1) {parent->_balanceFactor = 0;subL->_balanceFactor = -1;}else if (balanceFactor == 0) {parent->_balanceFactor = 0;subL->_balanceFactor = 0;}else {assert(false);}}void InOrder() {_InOrder(_root);cout << endl;}int height() {int h = _height(_root);return h;}int size() {int s = _size(_root);return s;}bool IsBalance() {return _IsBalance(_root);}private:bool _IsBalance(Node* root) {if (root == nullptr)return true;int leftHeight = _height(root->_left);int rightHeight = _height(root->_right);if (abs(leftHeight - rightHeight) >= 2)return false;if (abs(root->_balanceFactor) >= 2)return false;return _IsBalance(root->_left) && _IsBalance(root->_right);}int _height(Node* root) {if (root == nullptr)return 0;int left = _height(root->_left);int right = _height(root->_right);int height = max(left, right);return height + 1;}int _size(Node* root) {if (root == nullptr)return 0;return _size(root->_left) + _size(root->_right) + 1;}void _InOrder(Node* root) {if (root == nullptr) return;_InOrder(root->_left);cout << root->_kv.first << " " << root->_kv.second << endl;_InOrder(root->_right);}
private:Node* _root = nullptr;
};

AVL 树的概念于抽象数据结构

        一颗 AVL 树是空树或者是具有以下性质的二叉搜索树：

        1. 它的左右子树都是 AVL 树

        2. 左右子树的高度之差（平衡因子）的绝对值不超过 1

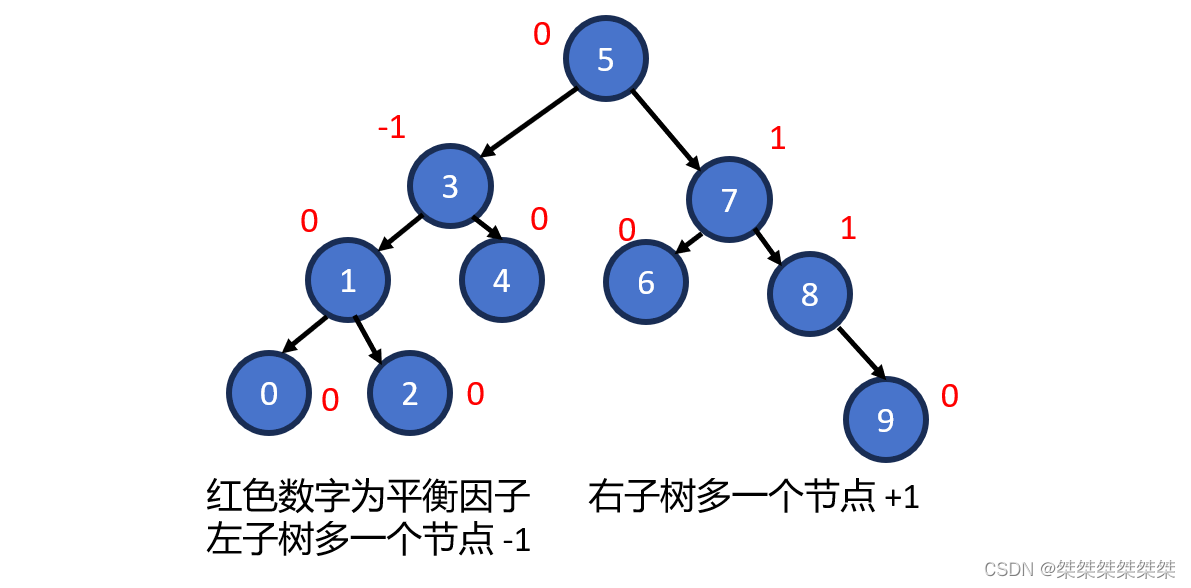
        左右子树的高度差不超过 1，可以降低树的高度，减少平均搜索长度。如下：

        关于 AVL 树的抽象数据结构，我们首先需要抽象出 AVL 树节点的数据结构，在 AVL 树中，我们存储的关键数据为键值对 pair，AVL 树节点中的平衡因子。然后需要一个指向左子树的指针，指向右子树的指针同时还需要一个指向父节点的指针，可以让我们便于更新每个节点的平衡因子。如下：

template <class K, class V>
struct AVLTreeNode {AVLTreeNode<K, V>* _left;AVLTreeNode<K, V>* _right;AVLTreeNode<K, V>* _parent;pair<K, V> _kv;int _balanceFactor;AVLTreeNode(const pair<K, V>& kv):_left(nullptr), _right(nullptr), _parent(nullptr), _kv(kv), _balanceFactor(0){}
};

AVL 树的插入

        关于 AVL 树而言，只是在二叉搜索树的基础上引入了平衡因子，所以 AVL 树也可以看出二叉搜索树（左右高度差不大于1的二叉搜索树），所以对于 AVL 树的插入，可以分为以下两步：

        1. 按照二叉搜索树的方式插入新节点。

        2. 调整节点的平衡因子。

        所以我们插入节点，只需要找到应该插入的位置，然后插入即可，寻找插入位置按照：键值小于当前节点，向左子树搜索，键值大于当前节点，向右子树搜索的原则，直到找到空节点为止，就是应该插入的位置。寻找的时候，还需要记录下每一次搜索的父节点，便于链接指针，如下：

bool insert(const pair<K, V>& kv) {if (_root == nullptr) {_root = new Node(kv);return true;}// 开始查找Node* parent = nullptr;Node* cur = _root;while (cur) {if (cur->_kv.first < kv.first)parent = cur, cur = cur->_right;else if (cur->_kv.first > kv.first)parent = cur, cur = cur->_left;elsereturn false;}// cur == nullptrcur = new Node(kv);// 链接孩子节点和父节点if (parent->_kv.first > kv.first)parent->_left = cur;elseparent->_right = cur;cur->_parent = parent;// 需要更新平衡因子...return true;
}

        插入成功，则返回 true，插入失败（树中已经存在键值）则返回 false。

        以上只是完成了插入，插入元素之后，我们还需要更新节点的平衡因子，更新平衡因子按照以下原则进行更新：

        1. 插入元素位置位于父节点的右边，父节点的平衡因子 +1；        

        2. 插入元素位置位于父节点的左边，父节点的平衡因子 -1。

        3. 更新完父节点的平衡因子之后，父节点的平衡因子的取值可能为 0、正负1、正负2。

        5. 父节点的平衡因子更新完之后为0，不会影响父节点的父节点的平衡，所以不用在往上更新。

        6. 父节点的平衡因子跟新完之后为正负1，说明原来父节点的平衡因子为0，这时还会影响父节点的父节点的平衡因子，所以需要继续向上更新。当某个节点的平衡原则为正负二的时候，我们就需要通过选择使树平衡。

        如下：

// 需要更新平衡因子
// 如果是在父亲的左边，父亲的平衡因子减一、右边加一
if (parent->_left == cur)parent->_balanceFactor--;
elseparent->_balanceFactor++;
// 查看爷爷结点是否需要更新while (parent) {if (parent->_balanceFactor == 0) {break;}else if (parent->_balanceFactor == 1 || parent->_balanceFactor == -1) {if (parent == _root)break;// 现在的parent就不可能等于nullparent = parent->_parent;cur = cur->_parent;if (parent->_left == cur)parent->_balanceFactor--;elseparent->_balanceFactor++;}else if(parent->_balanceFactor == 2 || parent->_balanceFactor == -2) {if (parent->_balanceFactor == 2 && cur->_balanceFactor == 1)RotateLeft(parent);else if (parent->_balanceFactor == -2 && cur->_balanceFactor == -1)RotateRight(parent);else if (parent->_balanceFactor == -2 && cur->_balanceFactor == 1)RotateLeftRight(parent);else if (parent->_balanceFactor == 2 && cur->_balanceFactor == -1)RotateRightLeft(parent);elseassert(false);break;}else {assert(false);}
}

        对于如上的代码中，其中最难的一步就是旋转，关于旋转一共会出现四种情况：左单旋、右单旋、左右双旋、右左双旋。

AVL 树的旋转

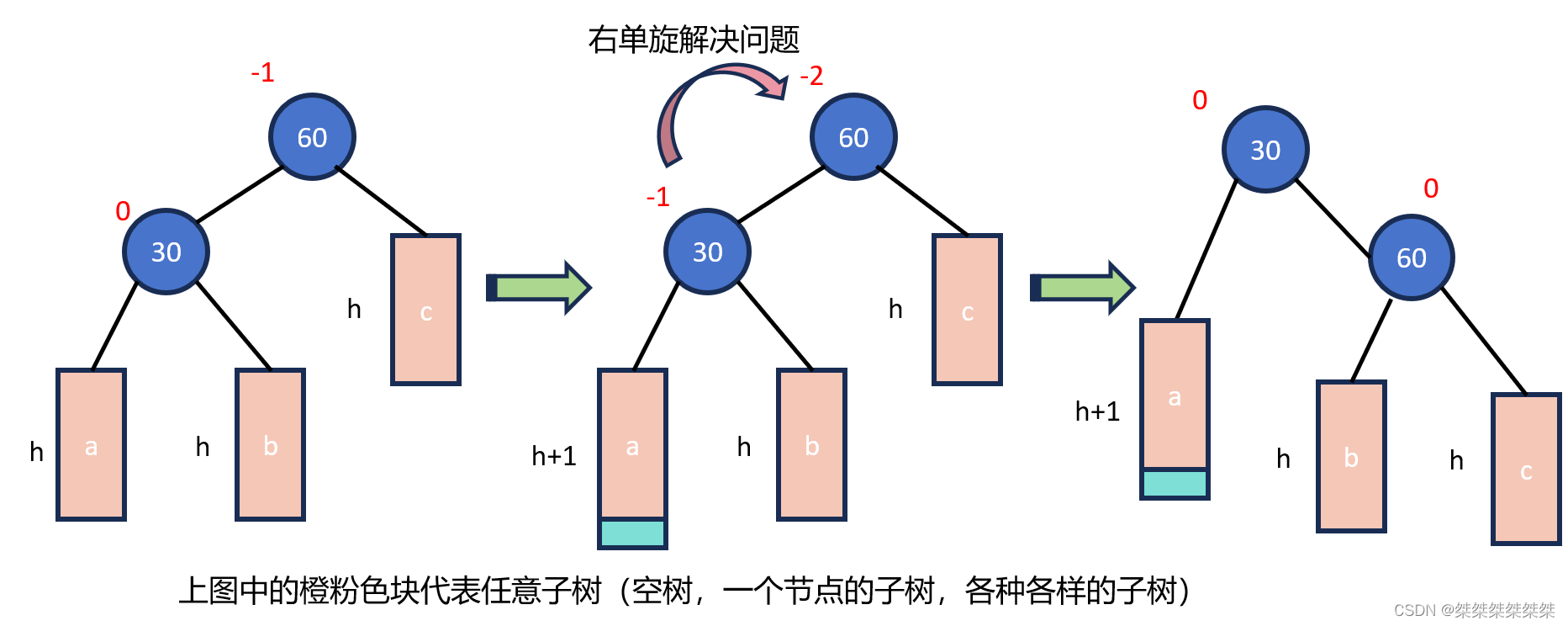
        我们首先介绍右单旋，当新节点插入导较高左子树的左侧就会出现右单旋，关于右单旋出现的情况如下：

        当出现如上所示的情况时（父亲节点的平衡因子等于-2，左孩子节点的平衡因子为-1时），我们就需要进行右旋，也就是将左孩子作为父节点，父节点作为右孩子，在将左孩子的右节点链接到原父节点上。其中还有需要注意的点：右旋时的父节点不一定是根节点，所以我们在旋转的时候，还需要记录下父节点的父节点，最后将其链接到一起。

void RotateRight(Node* parent) {Node* subL = parent->_left;Node* subLR = subL->_right;// 将左孩子的右节点链接到原父亲结点if (subLR) subLR->_parent = parent;parent->_left = subLR;Node* ppNode = parent->_parent;// 将左孩子变为原父亲结点的父亲subL->_right = parent;parent->_parent = subL;// 将爷爷结点重新链接if (ppNode == nullptr) {_root = subL;_root->_parent = nullptr;}else {if (ppNode->_left == parent)ppNode->_left = subL;elseppNode->_right = subL;subL->_parent = ppNode;}subL->_balanceFactor = parent->_balanceFactor = 0;
}

        记得最后将节点的平衡因子设置为0。

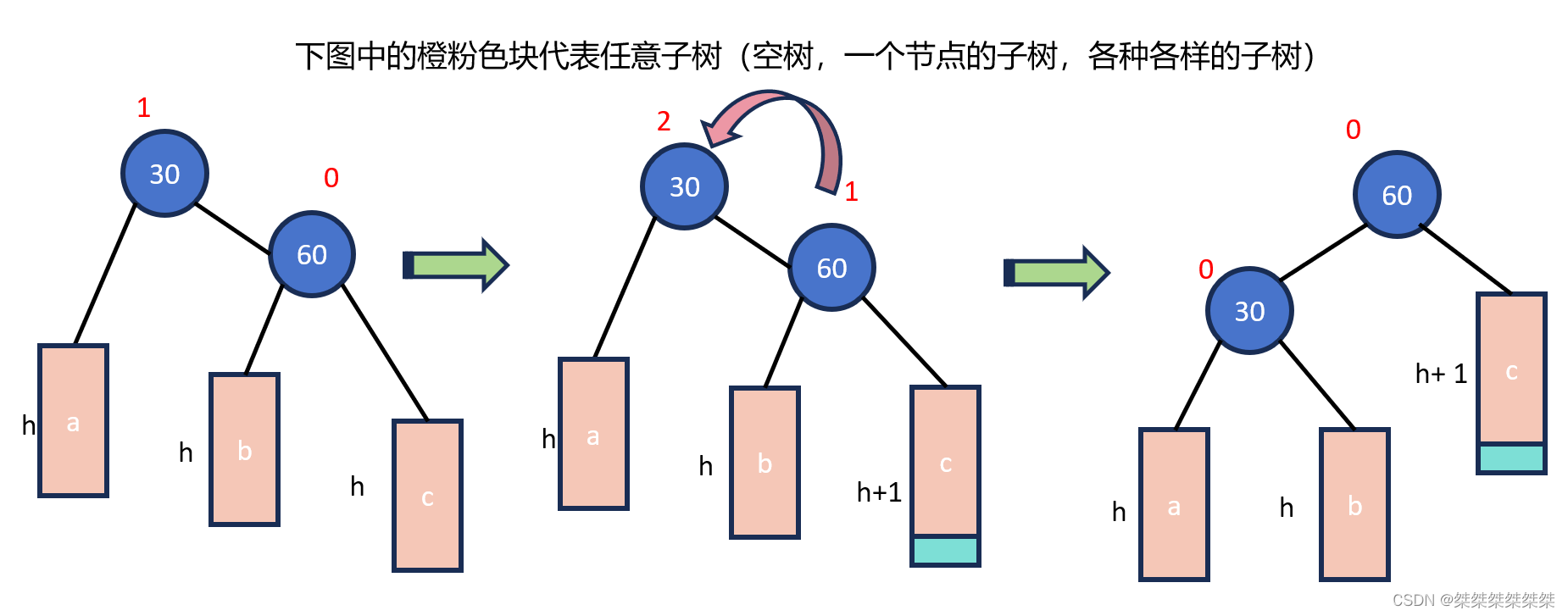
        接着我们介绍左单旋：当新节点插入到较高右子树的右侧，关于这种情况如下：

        关于左单旋，其思想和右单旋基本一致，不过是将右单旋的给镜像了过来。所以当父节点的平衡因子为2，右节点的平衡因子为1的时候，我们就需要对树进行左单旋。也就是让右孩子的左节点作为父节点的右孩子，左节点作为父节点，原父节点作为左孩子的左节点。注意原父节点的父节点是否为 nullptr，最后需要更新节点的平衡因子。如下：

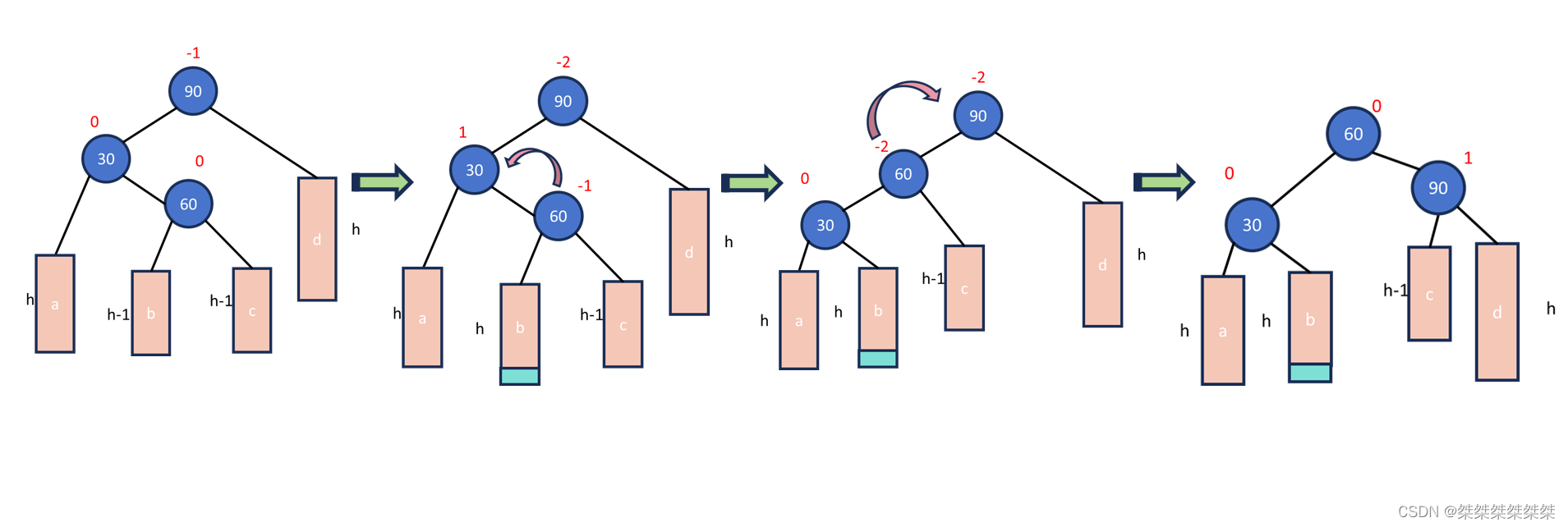
void RotateLeft(Node* parent) {Node* subR = parent->_right;Node* subRL = subR->_left;Node* ppNode = parent->_parent;parent->_right = subRL;if (subRL) subRL->_parent = parent;subR->_left = parent;parent->_parent = subR;if (ppNode == nullptr) {_root = subR;_root->_parent = nullptr;}else {if (ppNode->_left == parent)ppNode->_left = subR;elseppNode->_right = subR;subR->_parent = ppNode;}subR->_balanceFactor = parent->_balanceFactor = 0;
}

        第三种情况，左右双旋。左右双旋就是分别需要左旋一次，然后右旋一次，接着更新我们的平衡因子，如下：

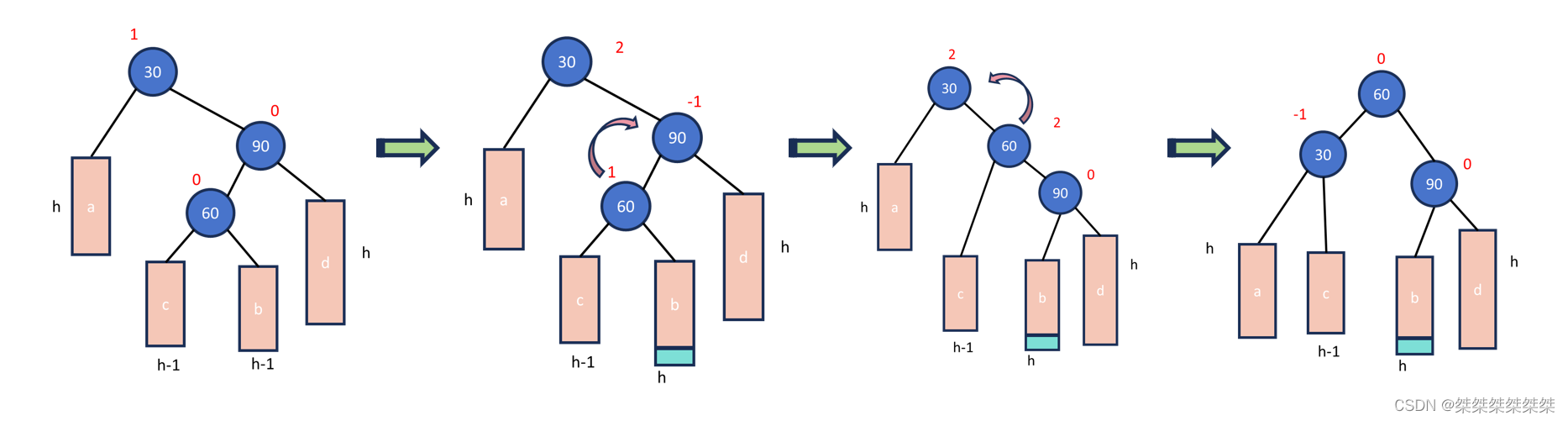
        如上图所示，当左孩子节点的平衡因子为1，父节点的平衡因子为-2的时候，我们就需要进行左右双旋，当我们旋转之后，当前父节点的平衡因子一定为0，但原父节点和左孩子节点的平衡因子一共有三种情况，分别是0 0，1 0，0 -1。当 h = 0 的时候，插入的节点就是以上的60节点，旋转之后所有节点（一共就3个节点）都是为0，当节点插入到60的左边，那么30的平衡因子为0（如图），当节点插入到60的右边，90的平衡因子则为0。

        因为在单独调用左单选，右单旋之后，会将所有节点的平衡因子都置为0，所以我们需要进行特殊处理。如下：

void RotateLeftRight(Node* parent) {Node* subL = parent->_left;Node* subLR = subL->_right;int balanceFactor = subLR->_balanceFactor;// 先左旋后右旋RotateLeft(subL);RotateRight(parent);subLR->_balanceFactor = 0;if (balanceFactor == -1) {subL->_balanceFactor = 0;parent->_balanceFactor = 1;}else if (balanceFactor == 1) {parent->_balanceFactor = 0;subL->_balanceFactor = -1;}else if (balanceFactor == 0) {parent->_balanceFactor = 0;subL->_balanceFactor = 0;}else {assert(false);}
}

        最后一种情况：右左双旋。也就是先右旋然后在左旋，也就是和以上的情况是堆成的情况，如下：

        对于需要右左旋转的情况为父节点为2，右孩子为1.关于转换的细节和以上的左右双旋的情况向对称，在这就不细讲了，代码如下：

void RotateRightLeft(Node* parent) {Node* subR = parent->_right;Node* subRL = subR->_left;int balanceFactor = subRL->_balanceFactor;RotateRight(subR);RotateLeft(parent);// 更新平衡因子subRL->_balanceFactor = 0;if (balanceFactor == -1) {parent->_balanceFactor = 0;subR->_balanceFactor = 1;}else if (balanceFactor == 1) {parent->_balanceFactor = -1;subR->_balanceFactor = 0;}else if (balanceFactor == 0) {parent->_balanceFactor = 0;subR->_balanceFactor = 0;}else {assert(false);}
}

AVL 树的验证 + 测试

        接下来我们将对我们是新的 AVL 树进行验证，也就是看我们写出的代码是否符合 AVL 树的特性，其中主要包括特性测试和压力测试。在进行测试之前，我们需要先写出一些辅助函数，如下：

template <class K, class V>
class AVLTree {
public:typedef AVLTreeNode<K, V> Node;void InOrder() {_InOrder(_root);cout << endl;}int height() {int h = _height(_root);return h;}int size() {int s = _size(_root);return s;}bool IsBalance() {return _IsBalance(_root);}private:bool _IsBalance(Node* root) {if (root == nullptr)return true;int leftHeight = _height(root->_left);int rightHeight = _height(root->_right);if (abs(leftHeight - rightHeight) >= 2)return false;if (abs(root->_balanceFactor) >= 2)return false;return _IsBalance(root->_left) && _IsBalance(root->_right);}int _height(Node* root) {if (root == nullptr)return 0;int left = _height(root->_left);int right = _height(root->_right);int height = max(left, right);return height + 1;}int _size(Node* root) {if (root == nullptr)return 0;return _size(root->_left) + _size(root->_right) + 1;}void _InOrder(Node* root) {if (root == nullptr) return;_InOrder(root->_left);cout << root->_kv.first << " " << root->_kv.second << endl;_InOrder(root->_right);}
private:Node* _root = nullptr;
};

        我们先进行特性测试，如下：

        如上所示，我们一共验证了两组数据，其中包含了左旋、右旋、左右双旋、右左双旋四种情况。

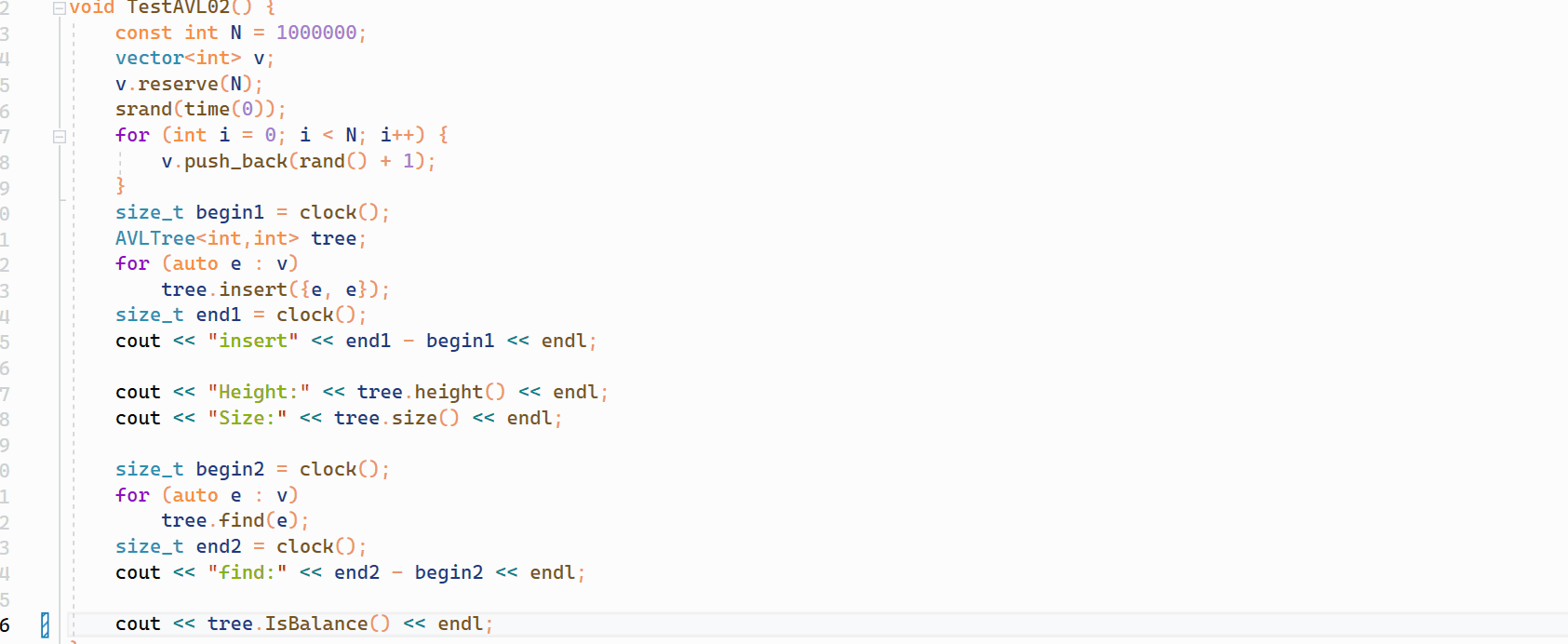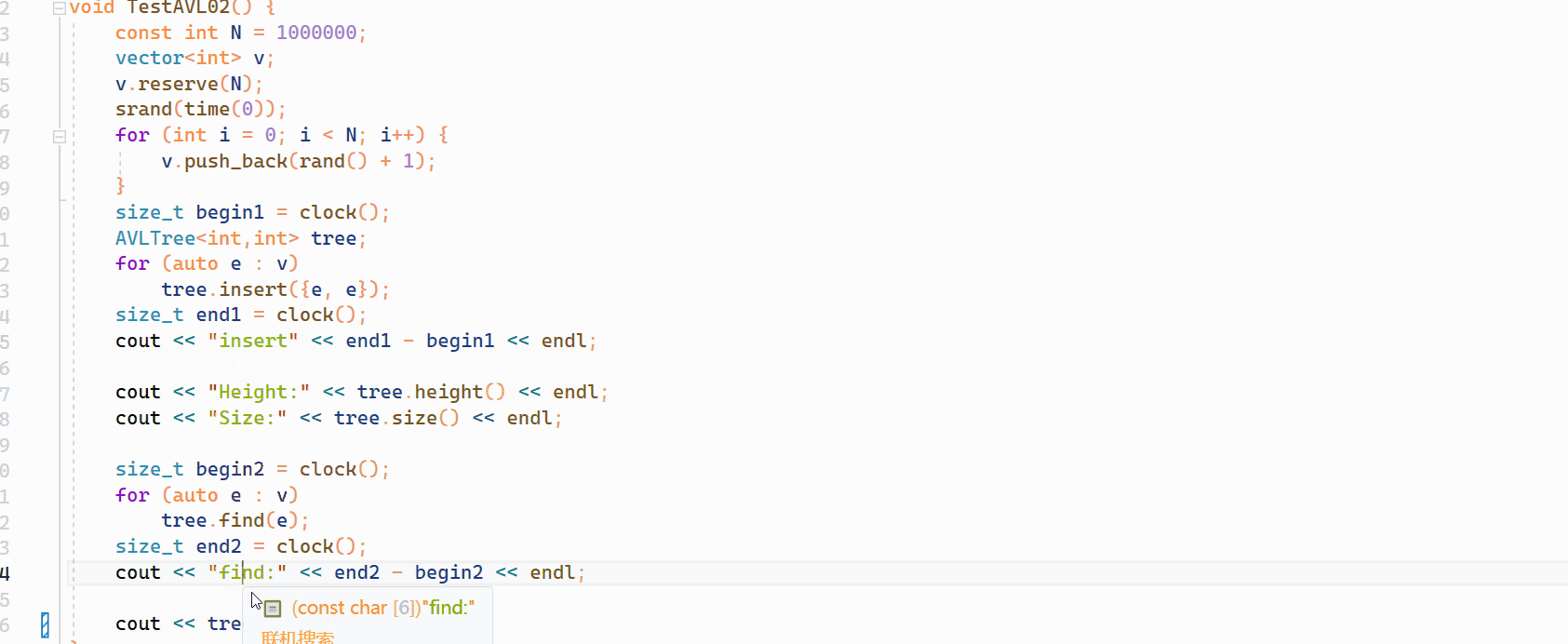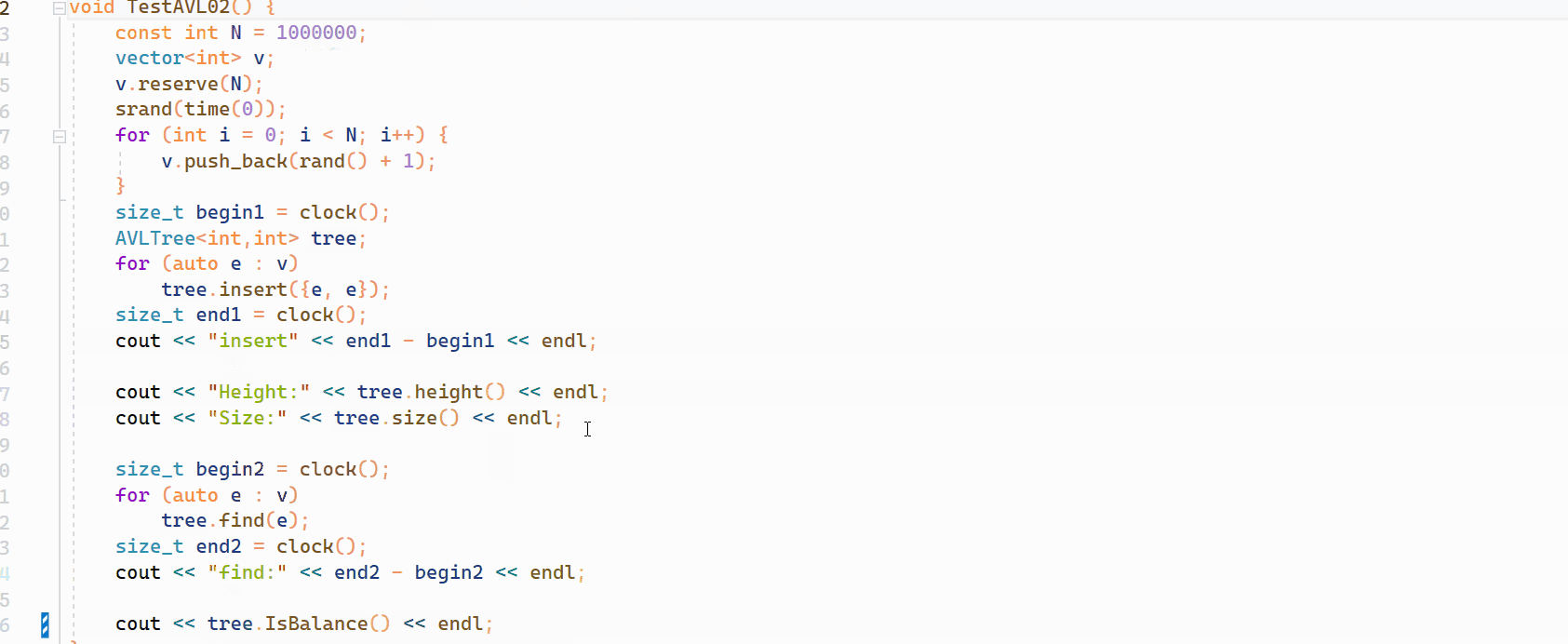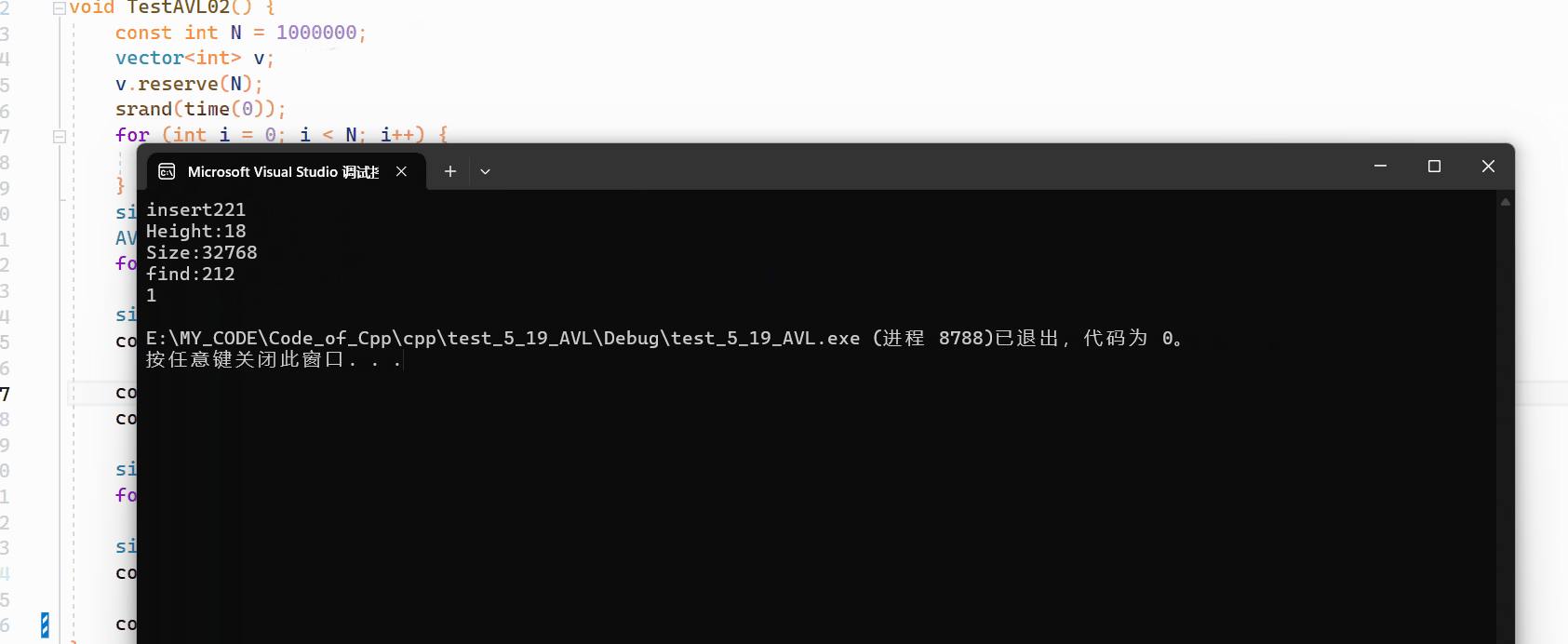
        接着进行暴力测试，生成一百万个数据，主要测试性能和插入是否成功：

        如上所示，插入一百万个数据也可以生成平衡树。

        测试源码如下：

void TestAVL01() {int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };// {16, 3, 7, 11, 9, 26, 18, 14, 15}AVLTree<int, int> avtree;for (auto e : a) {if (e == 4) {int i = 0;}avtree.insert(make_pair(e, e));}avtree.InOrder();cout << avtree.height() << endl;cout << avtree.size() << endl;cout << avtree.IsBalance() << endl;
}void TestAVL02() {const int N = 1000000;vector<int> v;v.reserve(N);srand(time(0));for (int i = 0; i < N; i++) {v.push_back(rand() + 1);}size_t begin1 = clock();AVLTree<int,int> tree;for (auto e : v)tree.insert({e, e});size_t end1 = clock();cout << "insert" << end1 - begin1 << endl;cout << "Height:" << tree.height() << endl;cout << "Size:" << tree.size() << endl;size_t begin2 = clock();for (auto e : v)tree.find(e);size_t end2 = clock();cout << "find:" << end2 - begin2 << endl;cout << tree.IsBalance() << endl;
}

这篇关于AVL树 ---（C++）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/1048132。

相关文章

【C++ Primer Plus习题】13.4

【C++ Primer Plus习题】13.4

大家好,这里是国中之林! ❥前些天发现了一个巨牛的人工智能学习网站，通俗易懂，风趣幽默，忍不住分享一下给大家。点击跳转到网站。有兴趣的可以点点进去看看← 问题: 解答: main.cpp #include <iostream>#include "port.h"int main() {Port p1;Port p2("Abc", "Bcc", 30);std::cout <<
阅读更多...
C++包装器

C++包装器

包装器 在 C++ 中，“包装器”通常指的是一种设计模式或编程技巧，用于封装其他代码或对象，使其更易于使用、管理或扩展。包装器的概念在编程中非常普遍，可以用于函数、类、库等多个方面。下面是几个常见的 “包装器” 类型： 1. 函数包装器 函数包装器用于封装一个或多个函数，使其接口更统一或更便于调用。例如，std::function 是一个通用的函数包装器，它可以存储任意可调用对象（函数、函数
阅读更多...
C++11第三弹：lambda表达式 | 新的类功能 | 模板的可变参数

C++11第三弹：lambda表达式 | 新的类功能 | 模板的可变参数

🌈个人主页： 南桥几晴秋 🌈C++专栏： 南桥谈C++ 🌈C语言专栏： C语言学习系列 🌈Linux学习专栏： 南桥谈Linux 🌈数据结构学习专栏： 数据结构杂谈 🌈数据库学习专栏： 南桥谈MySQL 🌈Qt学习专栏： 南桥谈Qt 🌈菜鸡代码练习： 练习随想记录 🌈git学习： 南桥谈Git 🌈🌈🌈🌈🌈🌈🌈🌈🌈🌈🌈🌈🌈�
阅读更多...
【C++】_list常用方法解析及模拟实现

【C++】_list常用方法解析及模拟实现

相信自己的力量，只要对自己始终保持信心，尽自己最大努力去完成任何事，就算事情最终结果是失败了，努力了也不留遗憾。💓💓💓 目录   ✨说在前面 🍋知识点一：什么是list？ •🌰1.list的定义 •🌰2.list的基本特性 •🌰3.常用接口介绍 🍋知识点二：list常用接口 •🌰1.默认成员函数 🔥构造函数（⭐） 🔥析构函数 •🌰2.list对象
阅读更多...
06 C++Lambda表达式

06 C++Lambda表达式

lambda表达式的定义 没有显式模版形参的lambda表达式 [捕获] 前属性 (形参列表) 说明符 异常 后属性 尾随类型 约束 {函数体} 有显式模版形参的lambda表达式 [捕获] <模版形参> 模版约束 前属性 (形参列表) 说明符 异常 后属性 尾随类型 约束 {函数体} 含义 捕获：包含零个或者多个捕获符的逗号分隔列表 模板形参：用于泛型lambda提供个模板形参的名
阅读更多...
6.1.数据结构-c/c++堆详解下篇（堆排序，TopK问题）

6.1.数据结构-c/c++堆详解下篇（堆排序，TopK问题）

上篇：6.1.数据结构-c/c++模拟实现堆上篇（向下，上调整算法，建堆，增删数据）-CSDN博客 本章重点 1.使用堆来完成堆排序 2.使用堆解决TopK问题 目录 一.堆排序 1.1 思路 1.2 代码 1.3 简单测试 二.TopK问题 2.1 思路(求最小)： 2.2 C语言代码（手写堆） 2.3 C++代码（使用优先级队列 priority_queue）
阅读更多...
【C++高阶】C++类型转换全攻略：深入理解并高效应用

【C++高阶】C++类型转换全攻略：深入理解并高效应用

📝个人主页🌹：Eternity._ ⏩收录专栏⏪：C++ “ 登神长阶 ” 🤡往期回顾🤡：C++ 智能指针 🌹🌹期待您的关注 🌹🌹 ❀C++的类型转换 📒1. C语言中的类型转换📚2. C++强制类型转换⛰️static_cast🌞reinterpret_cast⭐const_cast🍁dynamic_cast 📜3. C++强制类型转换的原因📝
阅读更多...
C++——stack、queue的实现及deque的介绍

C++——stack、queue的实现及deque的介绍

目录 1.stack与queue的实现 1.1stack的实现  1.2 queue的实现 2.重温vector、list、stack、queue的介绍 2.1 STL标准库中stack和queue的底层结构  3.deque的简单介绍 3.1为什么选择deque作为stack和queue的底层默认容器  3.2 STL中对stack与queue的模拟实现 ①stack模拟实现
阅读更多...
c++的初始化列表与const成员

c++的初始化列表与const成员

初始化列表与const成员 const成员 使用const修饰的类、结构、联合的成员变量，在类对象创建完成前一定要初始化。 不能在构造函数中初始化const成员，因为执行构造函数时，类对象已经创建完成，只有类对象创建完成才能调用成员函数，构造函数虽然特殊但也是成员函数。 在定义const成员时进行初始化，该语法只有在C11语法标准下才支持。 初始化列表 在构造函数小括号后面，主要用于给
阅读更多...
2024/9/8 c++ smart

2024/9/8 c++ smart

1.通过自己编写的class来实现unique_ptr指针的功能 #include <iostream> using namespace std; template<class T> class unique_ptr { public:         //无参构造函数         unique_ptr();         //有参构造函数         unique_ptr(
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2