逆序对计算的思考 (Tsinghua OJ,PA1)

本文主要是介绍逆序对计算的思考 (Tsinghua OJ,PA1)，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

Tags:Blog

---

题目出自清华DSA的Programming Assignment作业灯塔(LightHouse)．

描述

海上有许多灯塔，为过路船只照明。

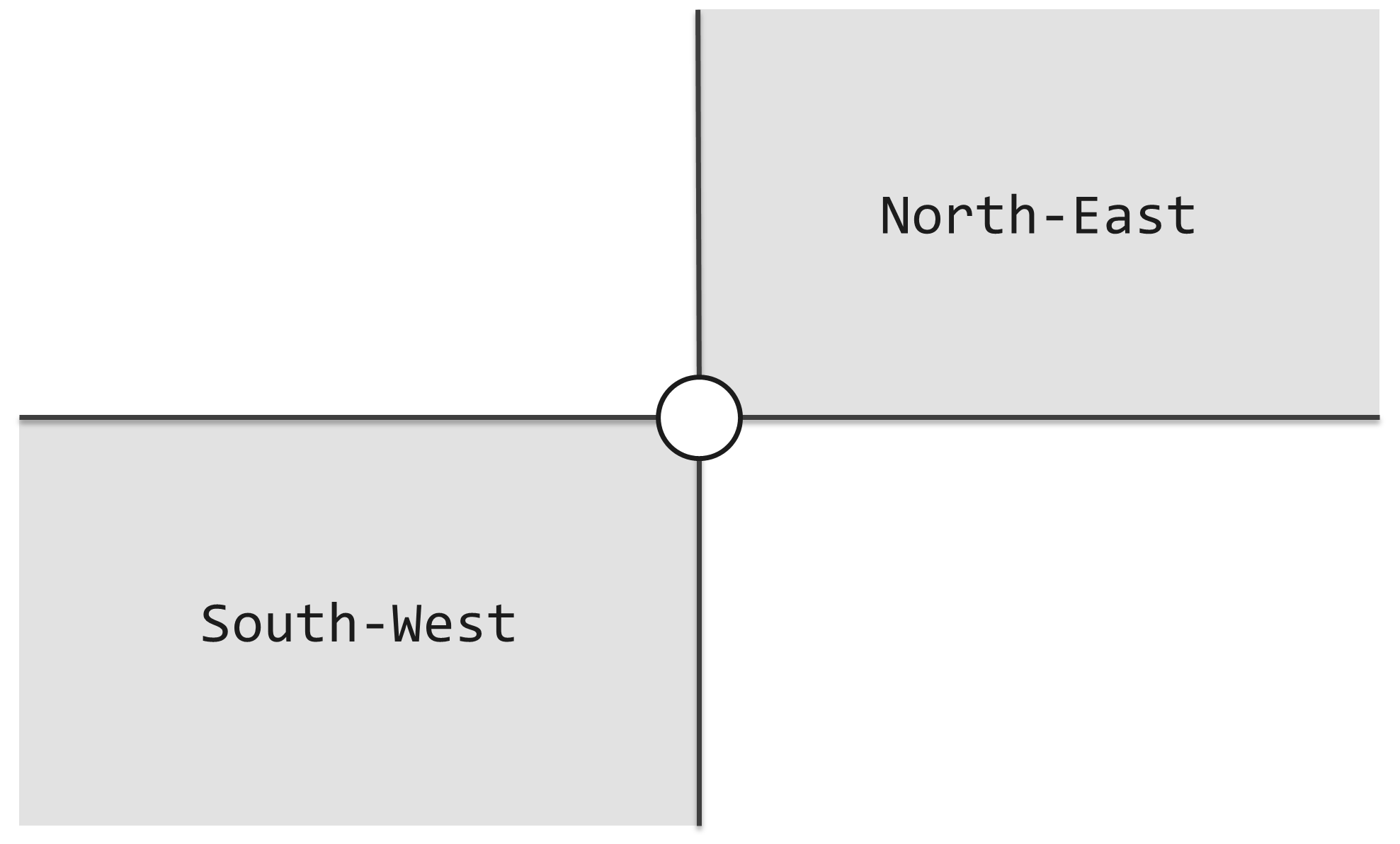
如图一所示，每个灯塔都配有一盏探照灯，照亮其东北、西南两个对顶的直角区域。探照灯的功率之大，足以覆盖任何距离。灯塔本身是如此之小，可以假定它们不会彼此遮挡。

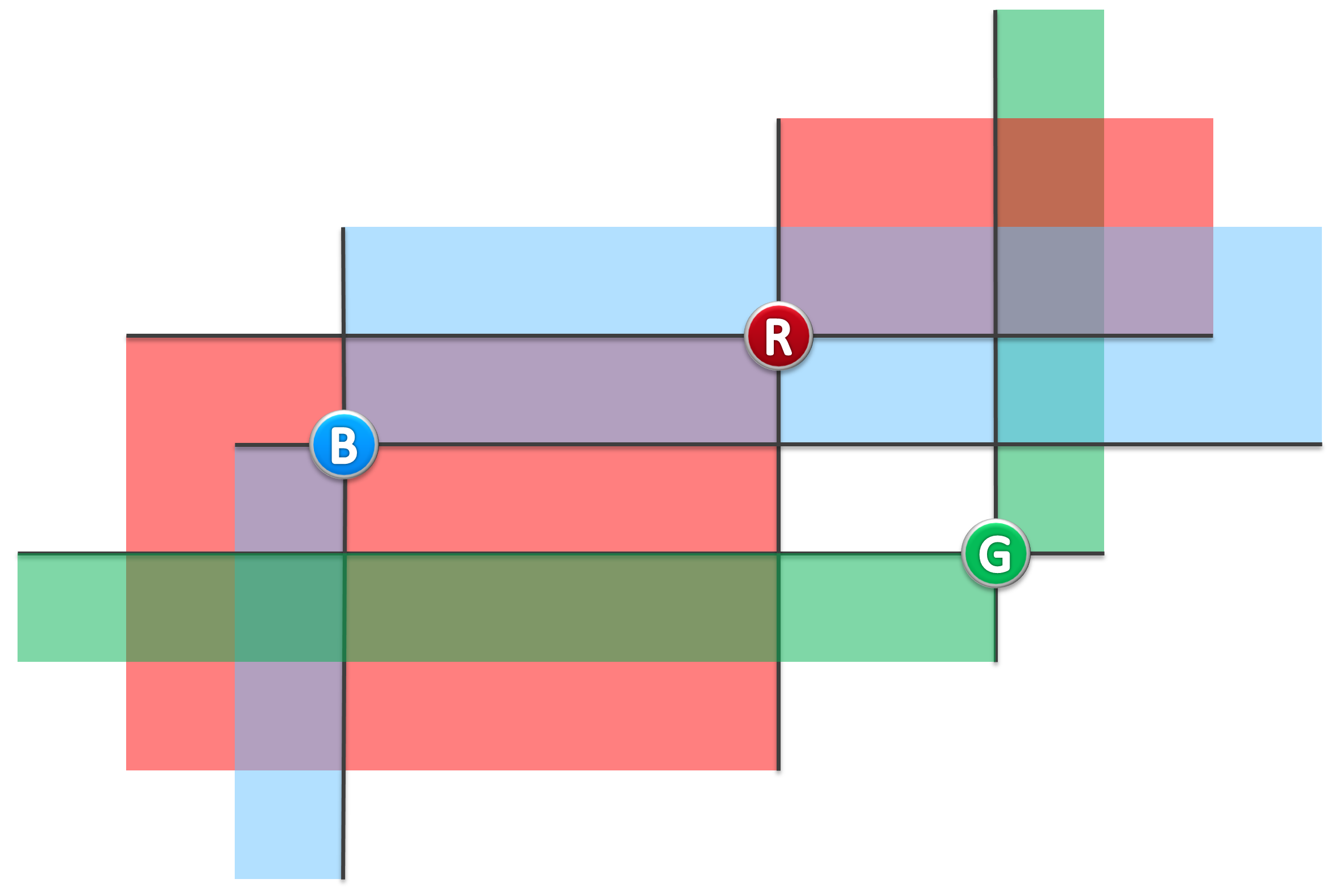
若灯塔A、B均在对方的照亮范围内，则称它们能够照亮彼此。比如在图二的实例中，蓝、红灯塔可照亮彼此，蓝、绿灯塔则不是，红、绿灯塔也不是。
现在，对于任何一组给定的灯塔，请计算出其中有多少对灯塔能够照亮彼此。

输入

共n+1行。
第1行为1个整数n，表示灯塔的总数。
第2到n+1行每行包含2个整数x, y，分别表示各灯塔的横、纵坐标。

输出

1个整数，表示可照亮彼此的灯塔对的数量。

样例

Input:

3
2 2
4 3
5 1

Output:

1

限制

对于90%的测例：1 ≤ n ≤ 3×10 5
对于95%的测例：1 ≤ n ≤ 10 6
全部测例：1 ≤ n ≤ 4×10 6
灯塔的坐标x, y是整数，且不同灯塔的x, y坐标均互异
1 ≤ x, y ≤ 10^8
时间：2 sec
内存：256 MB

提示

注意机器中整型变量的范围，C/C++中的int类型通常被编译成32位整数，其范围为[-231, 231 - 1]，不一定足够容纳本题的输出。

思考

我们把灯塔坐标抽象为坐标结构体
typedef struct pos{ long x,y; }Pos;
照亮的情况为一个灯塔在另一个灯塔的一四象限，即$tower1.x - tower2.x$与$tower1.y - tower2.y$同号．
思路一：通过检测每个元素和其他元素的配对情况解决．简单计算知时间复杂度

$$1 + 2 + 3 + \dots + (n-1) = O(n^2)$$
思路二：利用二维线段树求解　暂不详解@XJSoft
思路三：利用逆序对求解．
具体思路为先对Ｘ坐标排序，则排好序的数组中一定有 $tower\_pre.x < tower\_suc.x$
只要统计Ｙ坐标中前面的元素Ｙ坐标比后面的元素小的即可．则不难得到
$$X_y,Y_y逆序　\Leftrightarrow X,Y 互不可照亮$$
$$ans = n(n-1)-\tau(y_1y_2y_3\dots y_n)$$

如图，Ｘ已经排好序，Ｙ坐标为{2,1,3,4} 逆序对数量为１＋０＋０＋０＝１
总对数N(N - 1)对，其中不可照亮的有１对，可照亮的有N(N - 1) - 1 = 5对．

代码实现

经过多次优化，把$4\times10^6$的用例用1.3s　A掉了．

//CopyRight by XJSoft & ChestnutHeng.
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <time.h>
#include <math.h>
#include <sys/time.h>
#include <ctype.h>//#define DBG_FLAG    //检测用时
#define ISDIGIT(ch) (ch >= '0' && ch <= '9')
long long detect;
long long start_time;typedef struct pos   //灯塔结构体
{long x,y; 
}Pos;typedef struct parser_ {　//解释器，用于快速IOchar *buf;int pos;
} Parser;void read_line(Parser *parser, char *buffer) {gets(buffer);parser->buf = buffer;parser->pos = 0;
}void read_all(Parser *parser, char *buffer) {long sz = 0;long readed;
repeat:                             readed = fread(buffer + sz, 1, 100*1024*1024, stdin);  //100M的缓冲区,一次读完数据if (readed == 0) {buffer[sz] = '\0';goto final;}sz += readed;goto repeat;
final:parser->buf = buffer;parser->pos = 0;
}inline long parse_long(Parser *parser) {while(!(ISDIGIT(parser->buf[parser->pos]) || parser->buf[parser->pos] == '-')) {parser->pos++;}long ret = 0;int sign = 0;if (parser->buf[parser->pos] == '-') {sign = 1;parser->pos++;}while(ISDIGIT(parser->buf[parser->pos])) {ret = ret * 10 + (parser->buf[parser->pos] - '0');parser->pos++;}if (sign) {return -ret;}return ret;
}Pos *temp;
inline int compare(const void *p1, const void *p2) { //本来在Qsort中用的比较函数return (*(Pos*)p1).x - (*(Pos*)p2).x;
}long get_tick_count() {
#ifdef DBG_FLAGstruct timeval tv;gettimeofday(&tv, NULL);return tv.tv_sec * 1000 + tv.tv_usec / 1000;
#elsereturn 0;
#endif
}long read_long() {long ret = 0;while(1) {int ch = fgetc(stdin);if (isdigit(ch)) {ungetc(ch, stdin);break;}}while(1) {int ch = fgetc(stdin);if (isdigit(ch)) {ret = ret * 10 + (ch - '0');} else {return ret;}}
}void debug_time(const char *msg) {
#ifdef DBG_FLAGFILE *fp = fopen("time.log", "a");fprintf(fp, "[%lld] %s\n", get_tick_count() - start_time, msg);fclose(fp);
#endif
}inline long merge(Pos *array,int low,int mid,int high)
{int i = low,j = mid+1,k = low;long count = 0;while(i <= mid && j <= high)if(array[i].y <= array[j].y) {temp[k++] = array[i++];} else{temp[k++] = array[j++];count += j-k;   //逆序数计算}while(i <= mid)temp[k++] = array[i++];while(j <= high)temp[k++] = array[j++];long long st = get_tick_count();memcpy(array + low, temp + low, (high - low + 1) * sizeof(Pos)); //复制数组的优化detect += (get_tick_count() - st);return count;
}long mergeSort(Pos *array,int lo,int hi)
{if(lo<hi){int mid=(lo+hi)>>1;long count=0;count += mergeSort(array,lo,mid);count += mergeSort(array,mid+1,hi);count += merge(array,lo,mid,hi);return count;}return 0;
}void QuickSort(Pos *data, int low, int high) { //手写快排的优化if (low >= high) {return;}int pivot_item = low + rand() % (high - low + 1);Pos swp;swp = data[pivot_item];data[pivot_item] = data[high];data[high] = swp;Pos pivot = data[high];int i, j;i = low;for (j = low; j < high; ++j) {if (data[j].x <= pivot.x) {swp = data[i];data[i] = data[j];data[j] = swp;i++;}}swp = data[i];data[i] = data[high];data[high] = swp;QuickSort(data, low, i - 1);QuickSort(data, i + 1, high);
}int main()
{srand(time(NULL));detect = 0;start_time = get_tick_count();Pos * data = (Pos *)malloc(sizeof(Pos)*4000099);   //数据区debug_time("ALLOC.");int i;int t = 0;long n = 0;long ms;char *all_buf;all_buf = (char*)malloc(100*1024*1024);  //缓冲区Parser parser;read_all(&parser, all_buf);debug_time("RALL.");n = parse_long(&parser);Pos *pointer, *pend = data + n;for (pointer = data; pointer != pend; ++pointer) {  //用解释器读取数据pointer->x = parse_long(&parser);   pointer->y = parse_long(&parser);}free(all_buf);debug_time("READ.");QuickSort(data, 0, n - 1);//  qsort(data,n,sizeof(Pos),compare);#ifdef DBG_FLAGFILE *opt = fopen("sorted.txt", "w");for (pointer = data; pointer != pend; ++pointer) {fprintf(opt, "%ld %ld\n", pointer->x, pointer->y);}fclose(opt);
#endifdebug_time("SORT.");temp = (Pos *)malloc(sizeof(Pos)*4000099);ms = n*(n-1)/2 - mergeSort(data,0,n - 1);printf("%ld\n",ms);
#ifdef DBG_FLAGprintf("%lld\n", detect);
#endifdebug_time("MERGE.");free(data);free(temp);debug_time("ENDED.");return 0;
}

这篇关于逆序对计算的思考 (Tsinghua OJ,PA1)的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---