小波包的理解

小波变换	加窗Fourier变换	Fourier变换
突变信号或奇异性函数 自适应信号处理	处理渐变信号 实时信号处理	稳定和渐变信号 实时信号处理

2.小波包分解概述

传统的振动信号分析和处理方法一般都是采用加窗傅立叶分析，它是一个窗口函数固定不变的分析方法，无法反映信号的非平稳、持时短、时域和频域局部化等特性。
小波分析 是一种窗口面积固定但其形状可改变，即时间和频率窗都可改变的时频局部化分析方法，由于它在分解的过程中 只对低频信号再分解，对高频信号不再实施分解，使得它的频率分辨率随频率升高而降低。
在这种情况下，小波包分解应运而生，它不仅对低频部分进行分解，对高频部分也实施了分解，而且小波包分解能根据信号特性和分析要求自适应地选择相应频带与信号频谱相匹配，是一种比小波分解更为精细的分解方法。

3.爆破信号的小波包分解实例

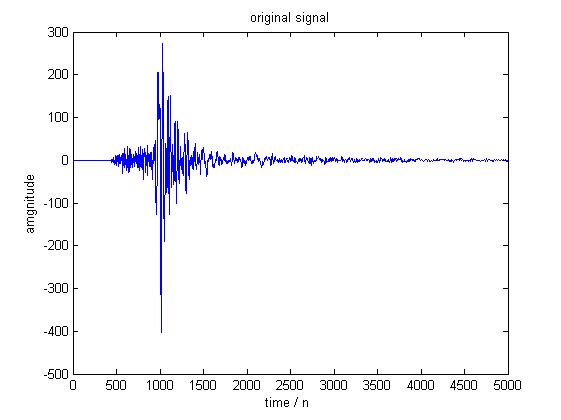
对其采用db5 小波，进行3 层分解。分解树如下图：所示，左边为三层分解树，右边为点击相应节点得到的分解系数，图示为原始信号（节点（0，0））。根据信号的采样频率即可得每一个分解节点的频带范围，例如假设本里中数据的采样频率为1024Hz，则奈奎斯特频率为512 Hz。则进行三层分解时，共分为2^3 = 8 个频带，每个频带的带宽为512/8 = 64Hz。因此节点（3，0）的频带范围为0~64 Hz，节点（3.1） 的频带范围为65~128 Hz

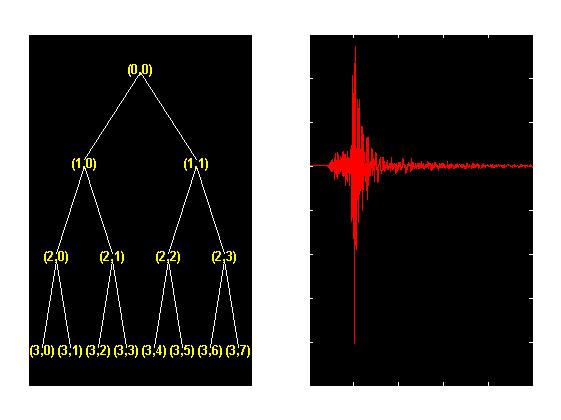
分解后每个节点的小波包系数如图所示:

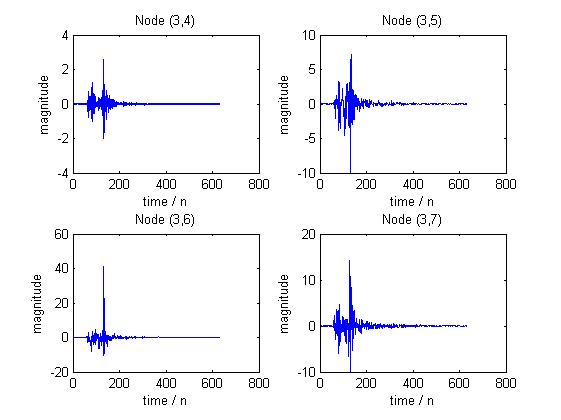
由此可见，原信号的主要能量集中在前两个频带内，即0~64Hz 和65~128 Hz 内。（观看信号的幅度）