AVL树、B树、B+树对比

本文主要是介绍AVL树、B树、B+树对比，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

文章目录

- 1.B树
- 2.B+树
- 3.AVL树
- 4.红黑树
- 5.面试常考

1.B树

B树又名平衡多路查找树（查找路径不只两个），不同于常见的二叉树，它是一种多叉树，我们常见的使用场景一般是在数据库索引技术里，大量使用者B树和B+树的数据结构。

B树大多用在磁盘上用于查找磁盘的地址。

因为磁盘会有大量的数据，有可能没有办法一次将需要的所有数据加入到内存中，所以只能逐一加载磁盘页，每个磁盘页就对应一个节点，而对于B树来说，B树很好的将树的高度降低了，这样就会减少IO查询次数，虽然一次加载到内存的数据变多了，但速度绝对快于AVL或是红黑树的。

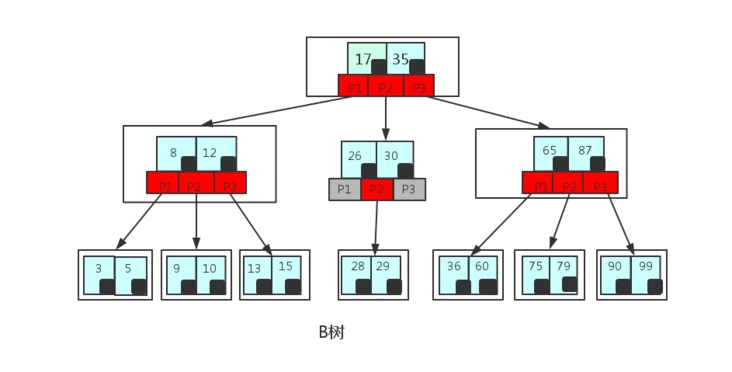
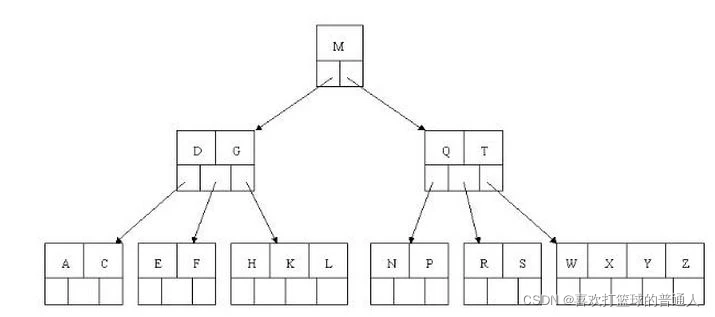
B树查询流程：要从下图中找到E字母，查找流程如下：

（1）获取根节点的关键字进行比较，当前根节点关键字为M，E<M（26个字母顺序），所以往找到指向左边的子节点（二分法规则，左小右大，左边放小于当前节点值的子节点、右边放大于当前节点值的子节点）；
（2）拿到关键字D和G，D<E<G 所以直接找到D和G中间的节点；
（3）拿到E和F，因为E=E 所以直接返回关键字和指针信息（如果树结构里面没有包含所要查找的节点则返回null）；
图片如下：

2.B+树

B+树时B树的一种升级版本，B+树查找的效率要比B树更高、更稳定。

B+树是应文件系统所需而产生的一种B树的变形树(文件的目录作为一级一级的索引，只有最底层的叶子节点(文件)保存数据)

非叶子节点只保存索引不保存实际的数据。
数据都保存在叶子节点中。
B+树的查找类似于文件系统文件的查找
eg：
有3个文件夹,a,b,c；
a包含b，b包含c，一个文件yang；
a,b,c就是索引(存储在非叶子节点)，a,b,c只是要找到的yang的key，而实际的数据yang存储在叶子节点上；

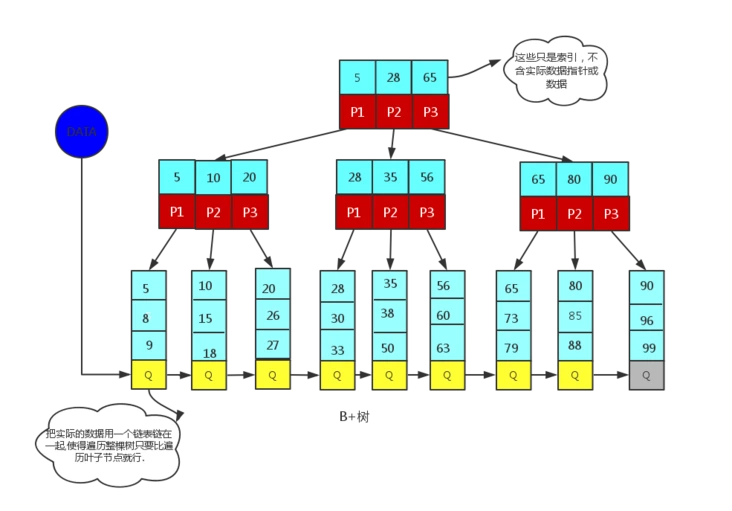
B+树与B树对比
B+树的特点如下：

所有叶子结点有一个链指针，所有关键字都在叶子结点出现，只有叶子节点有Data域
B+树的层级更少：相较于B树，B+树的每个非叶子节点存储的关键字数更多，树的层级更少所以查询数据更快；
B+树查询速度更稳定：B+所有关键字数据地址都存在叶子节点上，所以每次查找的次数都相同，其查询速度要比B树更稳定;
B+树天然具备排序功能：B+树所有的叶子节点数据构成了一个有序链表，在查询大小区间的数据时候更方便，数据紧密性很高，缓存的命中率也会比B树高。
B+树全节点遍历更快：B+树遍历整棵树只需要遍历所有的叶子节点即可，而不需要像B树一样需要对每一层进行遍历，这有利于数据库做全表扫描。

3.AVL树

AVL、红黑树是对二叉搜索树的改进版本。

平衡因子：节点的左右子树深度之差。

在一棵平衡二叉树中，节点的平衡因子只能取 0 、1 或者 -1 ，分别对应着左右子树等高，左子树比较高，右子树比较高。
AVL树是带有平衡条件的二叉查找树，一般是用平衡因子差值判断是否平衡并通过旋转来实现平衡，左右子树树高不超过1，和红黑树相比，它是严格的平衡二叉树，平衡条件必须满足（所有节点的左右子树高度差不超过1）。

不管我们是执行插入还是删除操作，只要不满足上面的条件，就要通过旋转来保持平衡，而旋转是非常耗时的，由此我们可以知道AVL树适合用于插入删除次数比较少，但查找多的情况。

由下图所知：任意节点的左右子树的平衡因子差值都不会大于1

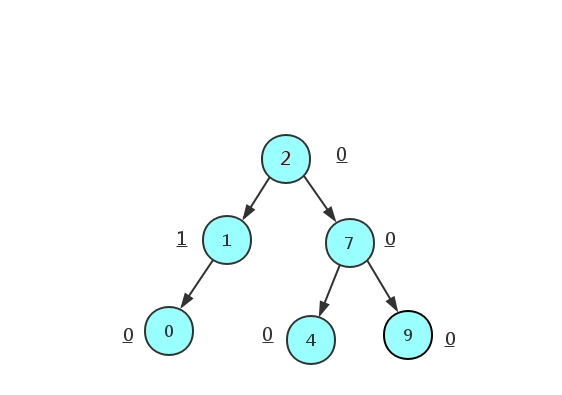
AVL树的局限性

由于维护这种高度平衡所付出的代价比从中获得的效率收益还大，故而实际的应用不多。
更多的地方是用追求局部而不是非常严格整体平衡的红黑树.
如果应用场景中对插入删除不频繁，只是对查找要求较高，那么AVL还是较优于红黑树

4.红黑树

一种二叉查找树，但在每个节点增加一个存储位表示节点的颜色，可以是red或black（非红即黑）

通过对任何一条从根到叶子的路径上各个节点着色的方式的限制，红黑树确保没有一条路径会比其它路径长出两倍
它是一种弱平衡二叉树(由于是弱平衡，可以推出，相同的节点情况下，AVL树的高度低于红黑树)，相对于要求严格的AVL树来说，它的旋转次数少，所以对于搜索、插入、删除操作较多的情况下，我们就用红黑树。
eg：

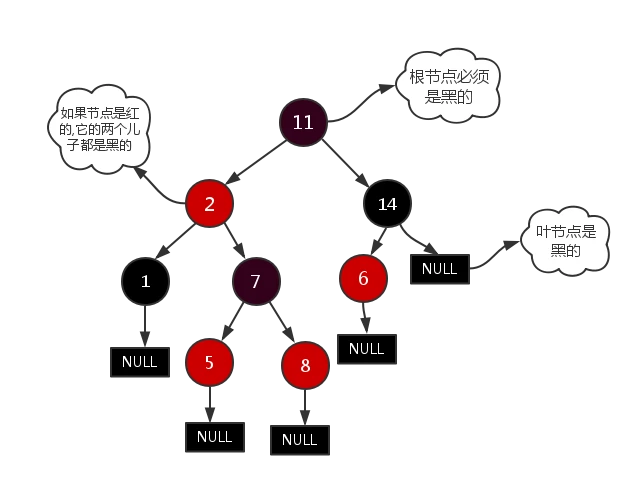
5.面试常考

1）为什么设计红黑树
红黑树通过它规则的设定，确保了插入和删除的最坏的时间复杂度是O(log N) 。

红黑树解决了AVL平衡二叉树的维护起来比较麻烦的问题，红黑树，读取略逊于AVL，维护强于AVL，每次插入和删除的平均旋转次数应该是远小于平衡树。

因此：

相对于要求严格的AVL树来说，红黑树的旋转次数少，所以对于插入、删除操作较多的情况下，我们就用红黑树。
但是，只是对查找要求较高，那么AVL还是较优于红黑树.

2）B树的作用
B树大多用在磁盘上用于查找磁盘的地址。

因为磁盘会有大量的数据，有可能没有办法一次将需要的所有数据加入到内存中，所以只能逐一加载磁盘页，每个磁盘页就对应一个节点，而对于B树来说，B树很好的将树的高度降低了，这样就会减少IO查询次数，虽然一次加载到内存的数据变多了，但速度绝对快于AVL或是红黑树的。

3）B树和 B+树的区别
其中B+树比B 树更适合实际应用中操作系统的文件索引和数据库索引。

B+树的磁盘读写代价更低
B+树的内部结点并没有指向关键字具体信息的指针。
B±tree的查询效率更加稳定
由于非终结点并不是最终指向文件内容的结点，而只是叶子结点中关键字的索引，所以任何关键字的查找必须走一条从根结点到叶子结点的路。
所有关键字查询的路径长度相同，导致每一个数据的查询效率相当。
B树在元素遍历的时候效率较低
由于B+树的数据都存储在叶子结点中，分支结点均为索引，方便扫库，只需要扫一遍叶子结点即可，但是B树因为其分支结点同样存储着数据，我们要找到具体的数据，需要进行一次中序遍历按序来扫，所以B+树更加适合在区间查询的情况，所以通常B+树用于数据库索引。
在数据库中基于范围的查询相对频繁，所以此时B+树优于B树

4）B树和红黑树的区别

最大的区别就是树的深度较高，在磁盘I/O方面的表现不如B树。
要获取磁盘上数据，必须先通过磁盘移动臂移动到数据所在的柱面，然后找到指定盘面，接着旋转盘面找到数据所在的磁道，最后对数据进行读写。磁盘IO代价主要花费在查找所需的柱面上，树的深度过大会造成磁盘IO频繁读写。
根据磁盘查找存取的次数往往由树的高度所决定。
所以，在大规模数据存储的时候，红黑树往往出现由于树的深度过大而造成磁盘IO读写过于频繁，进而导致效率低下。
在这方面，B树表现相对优异，B树可以有多个子女，从几十到上千，可以降低树的高度。

5）AVL树和红黑树的区别

AVL比RBtree更加平衡，但是AVL的插入和删除会带来大量的旋转。所以如果插入和删除比较多的情况，应该使用RBtree, 如果查询操作比较多，应该使用AVL。

6）数据库为什么使用B树，而不使用AVL或者红黑树
我们假设B+树一个节点可以有100个关键字，那么3层的B树可以容纳大概1000000多个关键字（100+101100+101101*100）。而红黑树要存储这么多至少要20层。所以使用B树相对于红黑树和AVL可以减少IO操作

7）mysql的Innodb引擎为什么采用的是B+树的索引方式
B+树只有叶子节点存放数据，而其他节点只存放索引，而B树每个节点都有Data域。

所以相同大小的节点B+树包含的索引比B树的索引更多（因为B树每个节点还有Data域）
还有就是B+树的叶子节点是通过链表连接的，所以找到下限后能很快进行区间查询，比B树中序遍历快

8）红黑树和 b+树的用途有什么区别？

红黑树多用在内部排序，即全放在内存中的，STL的map和set的内部实现就是红黑树。
B+树多用于外存上时，B+也被称之为一个磁盘友好的数据结构。

9）为什么B+树比B树更为友好

磁盘读写代价更低
树的非叶子结点里面没有数据，这样索引比较小，可以放在一个blcok（或者尽可能少的blcok）里面。
避免了树形结构不断的向下查找，然后磁盘不停的寻道，读数据。这样的设计，可以降低io的次数。
查询效率更加稳定
非终结点并不是最终指向文件内容的结点，而只是叶子结点中关键字的索引。
所以任何关键字的查找必须走一条从根结点到叶子结点的路。
所有关键字查询的路径长度相同，导致每一个数据的查询效率相当。
遍历所有的数据更方便
B+树只要遍历叶子节点就可以实现整棵树的遍历，而其他的树形结构要中序遍历才可以访问所有的数据。
参考：啥是二叉搜索树、B树、B+树、AVL树、红黑树，怎么那么多的树，一文全总结