Manacher解决最长回文子串

本文主要是介绍Manacher解决最长回文子串，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

问题描述

给定一个字符串，求解该字符串的最长回文子串

解法一

以字符串中的每个字符为中心，枚举其最长的回文子串，注意奇数和偶数长度的子串

int longPalindrome(char*str)
{int len = strlen(str);int maxlen = 1;for(int i = 0; i < len-1; i++){int j;for(j = 1; i - j >= 0 && i + j < len; j ++)if(str[i - j] != str[i + j])break;maxlen = maxlen > (j - 1) * 2 + 1 ? maxlen : (j - 1) * 2 + 1;for(j = 0; i - j >= 0 && i + j + 1 < len; j++)if(str[i-j] != str[i+j+1])break;maxlen = maxlen > 2 * j ? maxlen : 2 * j;}return maxlen;
}

Manacher

该算法为DP算法，我们可以保存上面中心扩展的结果来计算后面的点，如下图

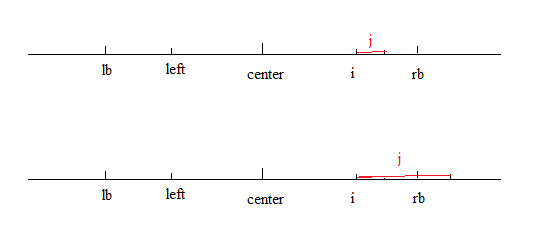
这里写图片描述
我们用f[i]表示以i为中心的最长的回文子串长度
如果我们从左到右得到位于center的结果f[center]了，那么现在计算以i为中心的f[i]
其中rb为以center为中心的最大右边界，left是i以center为对称的点
1. 当i + j < rb时，我们根据对称性，我们可以直接得到 f[ i ] = f[ left ]
2. 当i + j >= rb时，我们直接从rb位置开始扩展以i为中心的回文子串，同解法一方法一样扩展到最长位置

对于奇数和偶数的情况，我们在每两个字符之间插入一个特殊字符来进行处理，就可以统一奇数和偶数的处理了

如abababa变为#a#b#a#b#a#b#a#，在我们下面的算法中，直接用f[i]表示扩展时的j值，对于以i为中心的原始最长回文子串长度即为f[i]

int manacher(char*str)
{int len = strlen(str);int maxlen = 1;char helpstr[2 * len + 2];for(int i = 0; i <= len; i++){helpstr[2 * i] = '#';helpstr[2 * i + 1] = str[i];}int helplen = strlen(helpstr);int f[helplen];int center = 1;int rb = 2;f[0] = 0;f[1] = 1;for(int i = 2; i < helplen; i ++){if(i > rb)f[i] = 0;elsef[i] = (i + f[2 * center - i]) < rb ? f[2 * center - i] : center + f[center] - i;while(helpstr[i-f[i]-1] == helpstr[i+f[i]+1] && (i+f[i]+1) > rb && (i-f[i]-1) >= 0)f[i] ++;if(i + f[i] > rb){rb = i + f[i];center = i;}maxlen = maxlen > f[i] ? maxlen : f[i];}return maxlen;
}