HDU - 5047 Sawtooth

本文主要是介绍HDU - 5047 Sawtooth，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

Problem Description

Think about a plane:

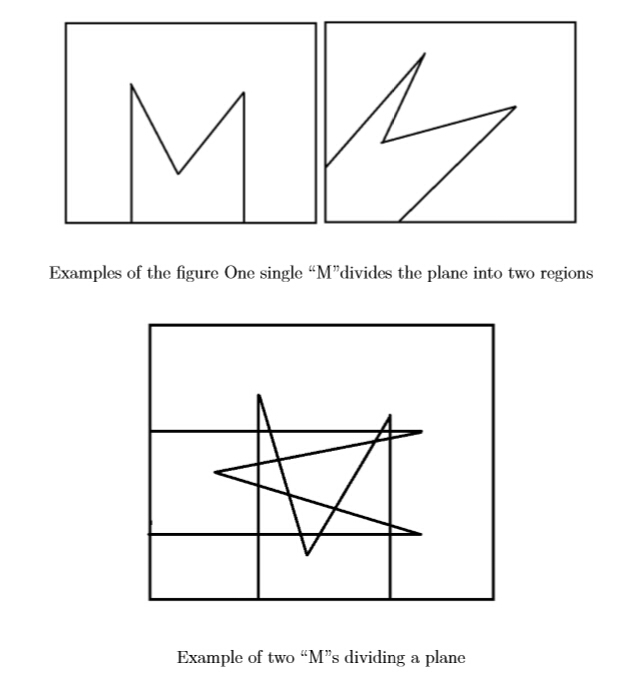
● One straight line can divide a plane into two regions.
● Two lines can divide a plane into at most four regions.
● Three lines can divide a plane into at most seven regions.
● And so on...

Now we have some figure constructed with two parallel rays in the same direction, joined by two straight segments. It looks like a character “M”. You are given N such “M”s. What is the maximum number of regions that these “M”s can divide a plane ?

Input

The first line of the input is T (1 ≤ T ≤ 100000), which stands for the number of test cases you need to solve.

Each case contains one single non-negative integer, indicating number of “M”s. (0 ≤ N ≤ 10 ¹²)

Output

For each test case, print a line “Case #t: ”(without quotes, t means the index of the test case) at the beginning. Then an integer that is the maximum number of regions N the “M” figures can divide.

Sample Input

  2
1
2

Sample Output

  Case #1: 2
Case #2: 19

题意：求n个m形能将空间最多化成几部分。
思路：每个m形都尽量去穿过前n-1个m，推出公式得：8*n^2-7*n+1,利用C++大数模板处理，加上输入外挂，Java卡时间。

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;typedef long long ll;/** 完全大数模板* 输出cin>>a* 输出a.print();* 注意这个输入不能自动去掉前导0的，可以先读入到char数组，去掉前导0，再用构造函数。* by kuangbin GG.*/
#define MAXN 9999
#define MAXSIZE 1010
#define DLEN 4
class BigNum
{private:int a[500]; //可以控制大数的位数int len;public:BigNum(){len=1;memset(a,0,sizeof(a));} //构造函数BigNum(const ll); //将一个int类型的变量转化成大数BigNum(const char*); //将一个字符串类型的变量转化为大数BigNum(const BigNum &); //拷贝构造函数BigNum &operator=(const BigNum &); //重载赋值运算符，大数之间进行赋值运算friend istream& operator>>(istream&,BigNum&); //重载输入运算符friend ostream& operator<<(ostream&,BigNum&); //重载输出运算符BigNum operator+(const BigNum &)const; //重载加法运算符，两个大数之间的相加运算BigNum operator-(const BigNum &)const; //重载减法运算符，两个大数之间的相减运算BigNum operator*(const BigNum &)const; //重载乘法运算符，两个大数之间的相乘运算BigNum operator/(const int &)const; //重载除法运算符，大数对一个整数进行相除运算BigNum operator^(const int &)const; //大数的n次方运算int operator%(const int &)const; //大数对一个int类型的变量进行取模运算bool operator>(const BigNum &T)const; //大数和另一个大数的大小比较bool operator>(const int &t)const; //大数和一个int类型的变量的大小比较void print(); //输出大数
};BigNum::BigNum(const ll b) //将一个int类型的变量转化为大数
{ll c,d=b;len=0;memset(a,0,sizeof(a));while(d>MAXN){c=d-(d/(MAXN+1))*(MAXN+1);d=d/(MAXN+1);a[len++]=c;}a[len++]=d;
}
BigNum::BigNum(const char *s) //将一个字符串类型的变量转化为大数
{int t,k,index,L,i;memset(a,0,sizeof(a));L=strlen(s);len=L/DLEN;if(L%DLEN)len++;index=0;for(i=L-1;i>=0;i-=DLEN){t=0;k=i-DLEN+1;if(k<0)k=0;for(int j=k;j<=i;j++)t=t*10+s[j]-'0';a[index++]=t;}
}
BigNum::BigNum(const BigNum &T):len(T.len) //拷贝构造函数
{int i;memset(a,0,sizeof(a));for(i=0;i<len;i++)a[i]=T.a[i];
}
BigNum & BigNum::operator=(const BigNum &n) //重载赋值运算符，大数之间赋值运算
{int i;len=n.len;memset(a,0,sizeof(a));for(i=0;i<len;i++)a[i]=n.a[i];return *this;
}
istream& operator>>(istream &in,BigNum &b)
{char ch[MAXSIZE*4];int i=-1;in>>ch;int L=strlen(ch);int count=0,sum=0;for(i=L-1;i>=0;){sum=0;int t=1;for(int j=0;j<4&&i>=0;j++,i--,t*=10){sum+=(ch[i]-'0')*t;}b.a[count]=sum;count++;}b.len=count++;return in;
}
ostream& operator<<(ostream& out,BigNum& b) //重载输出运算符
{int i;cout<<b.a[b.len-1];for(i=b.len-2;i>=0;i--){printf("%04d",b.a[i]);}return out;
}
BigNum BigNum::operator+(const BigNum &T)const //两个大数之间的相加运算
{BigNum t(*this);int i,big;big=T.len>len?T.len:len;for(i=0;i<big;i++){t.a[i]+=T.a[i];if(t.a[i]>MAXN){t.a[i+1]++;t.a[i]-=MAXN+1;}}if(t.a[big]!=0)t.len=big+1;else t.len=big;return t;
}
BigNum BigNum::operator-(const BigNum &T)const //两个大数之间的相减运算
{int i,j,big;bool flag;BigNum t1,t2;if(*this>T){t1=*this;t2=T;flag=0;}else{t1=T;t2=*this;flag=1;}big=t1.len;for(i=0;i<big;i++){if(t1.a[i]<t2.a[i]){j=i+1;while(t1.a[j]==0)j++;t1.a[j--]--;while(j>i)t1.a[j--]+=MAXN;t1.a[i]+=MAXN+1-t2.a[i];}else t1.a[i]-=t2.a[i];}t1.len=big;while(t1.a[len-1]==0 && t1.len>1){t1.len--;big--;}if(flag)t1.a[big-1]=0-t1.a[big-1];return t1;
}
BigNum BigNum::operator*(const BigNum &T)const //两个大数之间的相乘
{BigNum ret;int i,j,up;int temp,temp1;for(i=0;i<len;i++){up=0;for(j=0;j<T.len;j++){temp=a[i]*T.a[j]+ret.a[i+j]+up;if(temp>MAXN){temp1=temp-temp/(MAXN+1)*(MAXN+1);up=temp/(MAXN+1);ret.a[i+j]=temp1;}else{up=0;ret.a[i+j]=temp;}}if(up!=0)ret.a[i+j]=up;}ret.len=i+j;while(ret.a[ret.len-1]==0 && ret.len>1)ret.len--;return ret;
}
BigNum BigNum::operator/(const int &b)const //大数对一个整数进行相除运算
{BigNum ret;int i,down=0;for(i=len-1;i>=0;i--){ret.a[i]=(a[i]+down*(MAXN+1))/b;down=a[i]+down*(MAXN+1)-ret.a[i]*b;}ret.len=len;while(ret.a[ret.len-1]==0 && ret.len>1)ret.len--;return ret;
}
int BigNum::operator%(const int &b)const //大数对一个 int类型的变量进行取模
{int i,d=0;for(i=len-1;i>=0;i--)d=((d*(MAXN+1))%b+a[i])%b;return d;
}
BigNum BigNum::operator^(const int &n)const //大数的n次方运算
{BigNum t,ret(1);int i;if(n<0)exit(-1);if(n==0)return 1;if(n==1)return *this;int m=n;while(m>1){t=*this;for(i=1;(i<<1)<=m;i<<=1)t=t*t;m-=i;ret=ret*t;if(m==1)ret=ret*(*this);}return ret;
}
bool BigNum::operator>(const BigNum &T)const //大数和另一个大数的大小比较
{int ln;if(len>T.len)return true;else if(len==T.len){ln=len-1;while(a[ln]==T.a[ln]&&ln>=0)ln--;if(ln>=0 && a[ln]>T.a[ln])return true;elsereturn false;}elsereturn false;
}
bool BigNum::operator>(const int &t)const //大数和一个int类型的变量的大小比较
{BigNum b(t);return *this>b;
}
void BigNum::print() //输出大数
{int i;printf("%d",a[len-1]);for(i=len-2;i>=0;i--)printf("%04d",a[i]);printf("\n");
}ll Scan() {int ch, flag = 0;ll res = 0;if((ch = getchar()) == '-')flag = 1;else if(ch >= '0' && ch <= '9')res = ch - '0';while ((ch = getchar()) >= '0' && ch <= '9' )res = res * 10 + ch - '0';return flag ? -res : res;
}BigNum a, b, c, d;int main() {ll t, n;t = Scan();for (ll cas = 1; cas <= t; cas++) {a = BigNum(Scan());b = BigNum(8);c = BigNum(7);d = BigNum(1);a = a * a * b - a * c + d;printf("Case #%lld: ", cas);a.print();}return 0;
}