本文主要是介绍MT3049 区间按位与(ST表),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
MT3049 区间按位与(ST表)
题目描述
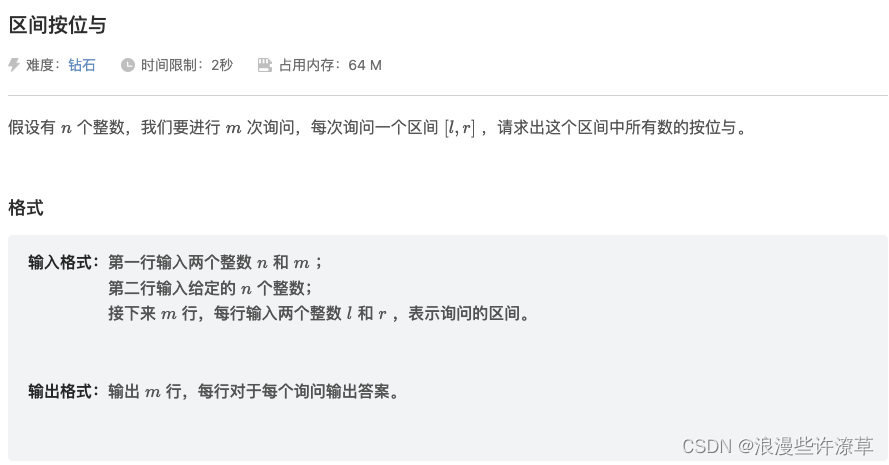


思路
这里先说一下我首先想到的思路,对区间进行操作,又是区间查询,所以我首先想到了线段树,于是一段回忆猛敲(copy),结果线段树是能做,但是数据量大了之后会TTL。。。
#include <iostream>
#include<stdio.h>
#include<string.h>
#include<algorithm>
using namespace std;const int MAXN=2e5+2;#define LL(x) (x<<1)
#define RR(x) (x<<1|1)struct segTree
{int le,ri;int val;int mid(){return (le+ri)>>1;}
}tree[MAXN<<2];int a[MAXN];void build(int rt,int le,int ri){tree[rt].le=le;tree[rt].ri=ri;if(le==ri){tree[rt].val=a[le];return ;}int mid=tree[rt].mid();build(LL(rt), le, mid);build(RR(rt), mid+1, ri);tree[rt].val=tree[LL(rt)].val|tree[RR(rt)].val;
}void update(){}int query(int rt,int le,int ri){if(tree[rt].le==le&&tree[rt].ri==ri)return tree[rt].val;int mid=tree[rt].mid();if(ri<=mid)return query(LL(rt),le,ri);else if(le>mid)return query(RR(rt),le,ri);elsereturn query(LL(rt),le,mid)|query(RR(rt),mid+1,ri);
}int main() {int n,m;scanf("%d %d",&n,&m);for(int i=1;i<=n;++i){scanf("%d",&a[i]);}build(1, 1, n);int l,r;while(m--){scanf("%d %d",&l,&r);printf("%d\n",query(1, l, r));}return 0;
}
然后看到这题的提示是ST表,没学过,于是记录一波。
个人理解,ST表就是预先打表,但是对于区间来说,打表过程优化了,类似于二分打表,查询过程也是优化的,最多查询两段,但是整体上必须要求数据中途不会被修改。
#include<iostream>
#include<stdio.h>
#include<string.h>
#include<algorithm>
using namespace std;const int MAXN=2e5+2;#define LL(x) (x<<1)
#define RR(x) (x<<1|1)int a[MAXN],mn[MAXN][50],lg[MAXN];
int n,m;// 求log
void pre(){lg[1]=0;for(int i=2;i<=n;++i){lg[i]=lg[i>>1]+1;}
}// 打表
void ST_init(){for(int i=1;i<=n;++i){mn[i][0]=a[i];}for(int j=1;j<=lg[n];++j)for(int i=1;i<=n-(1<<j)+1;++i)mn[i][j]=mn[i][j-1]&mn[i+(1<<(j-1))][j-1];
}// 查询
int ST_query(int l,int r){int k=lg[r-l+1];return mn[l][k]&mn[r-(1<<k)+1][k];
}int main() {scanf("%d %d",&n,&m);for(int i=1;i<=n;++i){scanf("%d",&a[i]);}pre();ST_init();int l,r;while(m--){scanf("%d %d",&l,&r);printf("%d\n",ST_query(l, r));}return 0;
}
这篇关于MT3049 区间按位与(ST表)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



