本文主要是介绍商品最大价值-第13届蓝桥杯选拔赛Python真题精选,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!

[导读]:超平老师的Scratch蓝桥杯真题解读系列在推出之后,受到了广大老师和家长的好评,非常感谢各位的认可和厚爱。作为回馈,超平老师计划推出《Python蓝桥杯真题解析100讲》,这是解读系列的第77讲。
商品最大价值,本题是2022年1月22日举办的第13届蓝桥杯青少组Python编程选拔赛真题编程部分第5题。小蓝桌子上摆放着一个容积为 m 的书包及n件不同的商品,且每件商品上都标有商品的体积和商品的价值,请编程计算出能装入书包的商品的最大价值。
先来看看题目的要求吧。
一.题目说明
编程实现:
小蓝桌子上摆放着一个容积为m的书包及n件不同的商品,且每件商品上都标有商品的体积和商品的价值。
小蓝要满足以下要求挑选商品装入书包中
要求 1:挑选的商品总体积不超过书包的容积;
要求 2:挑选的商品商品总价值最大。
请你帮助小蓝计算出能装入书包的商品的最大价值。
输入描述:
第一行输入两个正整数m和n,m表示书包的容积,n表示商品的数量。两个正整数之间一个英文逗号隔开
第二行输入n个正整数表示商品的体积,正整数之间一个英文逗号隔开
第三行输入n个正整数表示商品的价值,正整数之间一个英文逗号隔开(商品价值的输入顺序对应商品体积输入顺序)
输出描述:
输出装入书包的商品的最大价值
样例输入:
11,3
2,6,4
1,5,2
样例输出:
7
二.思路分析
这是一道算法题,涉及的知识点包括循环、列表、枚举算法和动态规划等。
很显然,这是一个典型的01背包问题,它是计算机科学和操作研究中经典的优化问题之一。
它的名称来源于这样一个情景:你有一个背包和一组物品,每个物品有一定的重量和价值;你需要在不超过背包最大负载的情况下,挑选出某些物品装进背包以使这些物品的总价值最大化。

针对本问题,我们有如下两种解决方案:
-
枚举算法
-
动态规划
我们分别来讨论。
1. 枚举算法
先来说说枚举算法,它是最简单的解决方案,我们可以使用combinations()函数将所有的组合列举出来,并找出总体积小于n的组合,计算出它们的总价值,然后就可以找出最大价值了。
以题目中给出的数据为例,3件商品,一共有7种不同的组合,我们可以使用表格列出所有的组合情况。
只挑选一件商品的组合情况如图所示:
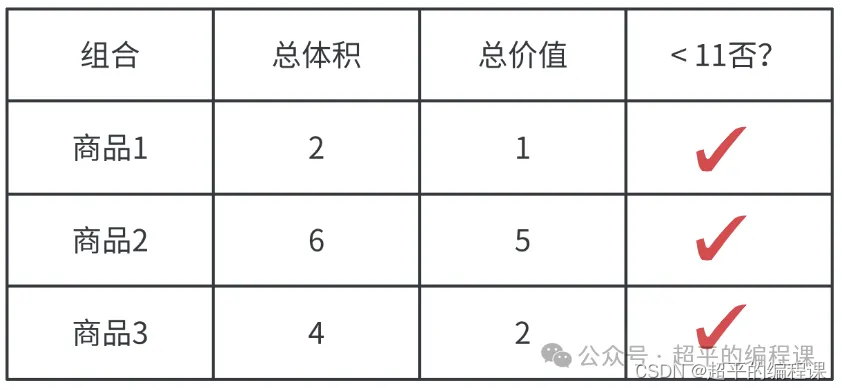
只挑选两件商品的组合情况如图所示:

挑选三件商品的组合情况如图所示:

通过上面的3个表格,可以发现,有6种组合满足条件,其中挑选商品2+商品3组合的总价值7是最高的。
2. 动态规划
使用动态规划算法的要点有如下4个:
-
定义DP数组
-
初始化DP数组
-
状态转移方程
-
遍历顺序
1). 定义DP数组
01背包是一个线性动态规划问题,我们可以定义一个二维列表dp[i][j],表示将前i个物品装入容积为j的书包中,所能得到的最大价值。
以题目中的数据为例,一共有3件商品,总体积为11,对应的二维表格如图所示:
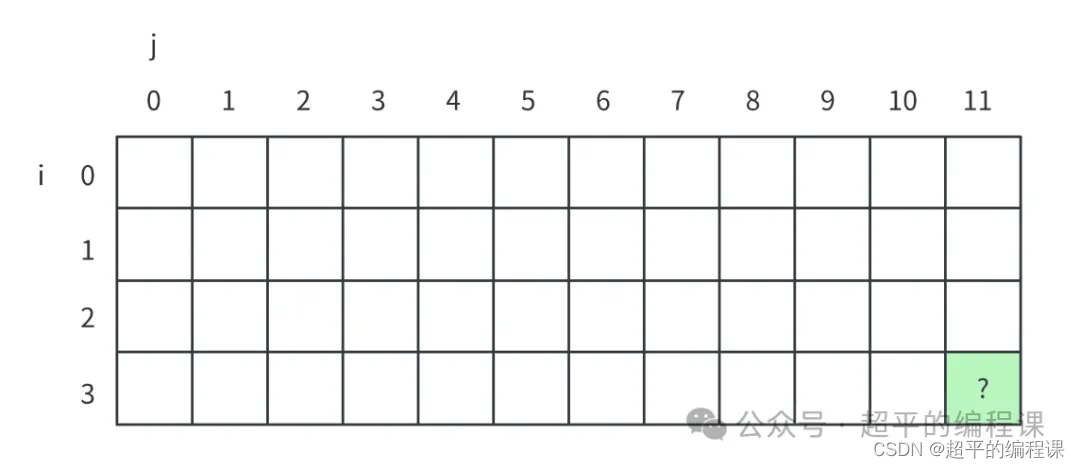
这里的行i表示要挑选的商品,列j表示书包的体积,而处在最右下角落的单元格dp[3][11],就是最终的答案。
需要注意的是,列的最大值是由书包容积m来决定的,并且是以最小整数单位1来递增的。
2). 初始化DP数组
为了方便计算,在上面的二维表格中,专门增加了i = 0的行、j = 0的列,前者表示没有挑选任何商品,后者表示容积为0。
因此,i = 0的行和j = 0的列,其最大价值均为0,如图:
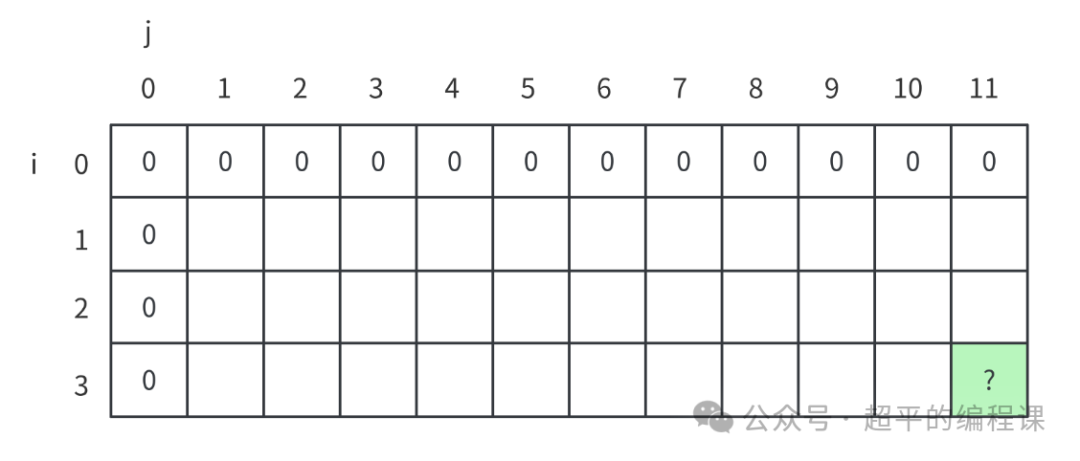
3). 状态转移方程
接下来,就是逐渐填表的过程,填写过程中,始终要牢记dp[i][j]的含义。
先从第一件商品开始,商品1的体积为2,价值为1。
单元格dp[1][1]表示将商品1装入体积为1的书包中的最大价值,很显然,由于1 < 2,说明无法装入,因此dp[1][1] = dp[0][1] = 0。
也就是说,如果无法装入商品1,那么它的值就和正上方的格子相同,如图所示:
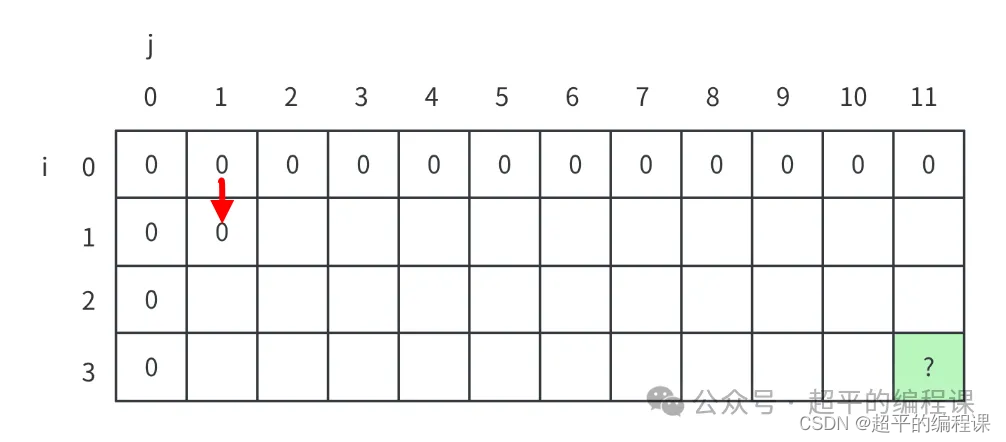
再来看dp[1][2],它表示将商品1装入体积为2的书包中的最大价值,此时2 = 2,可以装入,因此dp[1][2] = 1。
以此类推,可以发现,对于商品1,只要书包体积 >= 2,都可以装入,其最大价值都是1,对应的dp表格如图所示:
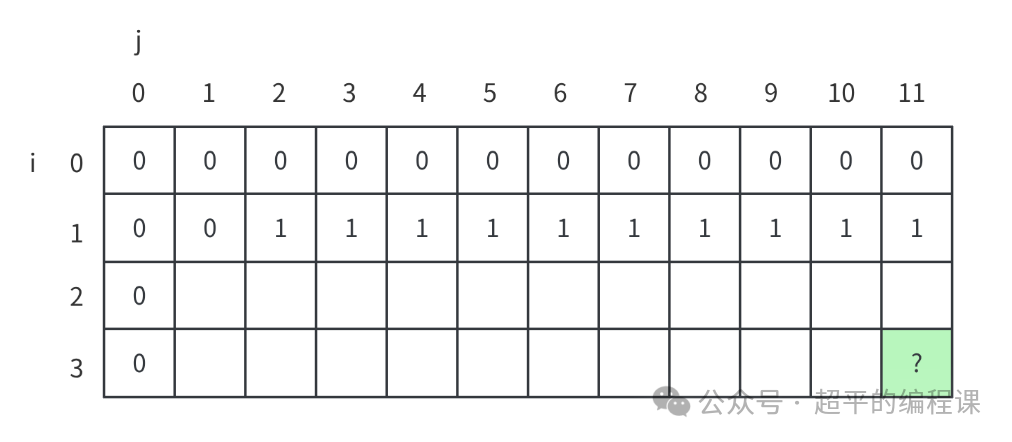
接下来,我们考虑第二件商品,商品2的体积为6,价值为5。
很显然,当书包体积小于6时,肯定是无法装入商品2,所以选择不装入,其值等于正上方的单元格,如图:

dp[2][6]会出现什么情况呢?
由于商品2的体积6刚好等于书包的容积,说明可以装入,此时就面临两种选择:
-
不装入
-
装入
如果不装入,就相当于在书包体积为6的书包中只装入前1个商品,因此dp[2][6] = dp[1][6] = 1。
如果装入,那么先考虑装入商品2的价值5,同时还要考虑装入商品2后,书包的剩余体积在装入前1个商品的最大价值。
换言之,装入商品2,还要考虑是否会把之前装入的商品挤出来,因为容积有限嘛。在这种情况下,dp[2][6] = 5 + dp[1][6-6] = 5 + dp[1][0] = 5。
然后,在上述两种情况下,选择最大值,很显然,5是最大价值,即装入商品2,此时商品1被挤出来了。
这个计算过程,如图所示:
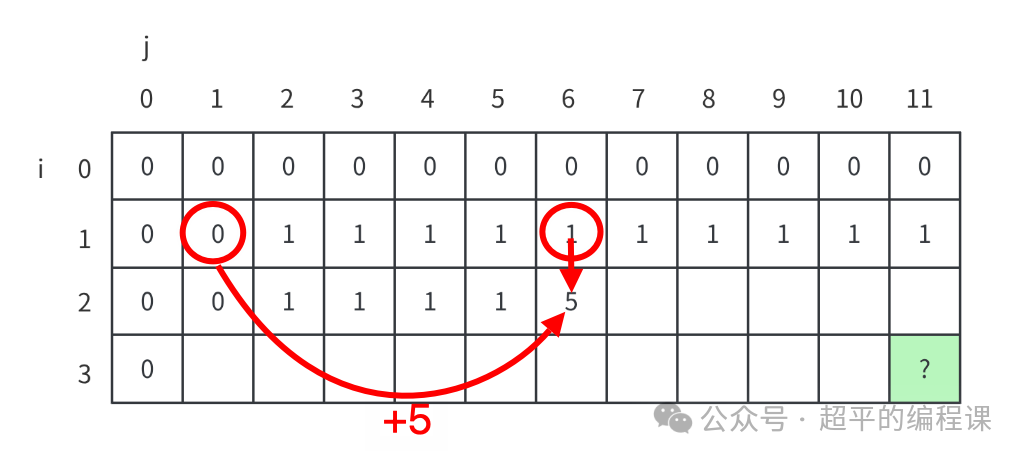
也就是说,我们需要在不装入和装入中选择价值最大的情况。到这里基本上就可以找到规律了,如下:
dp[i][j] = max(dp[i - 1][j],dp[i - 1][j - v[i]] + p[i])其中:v[i]表示当前商品的体积p[i]表示当前商品的价值
根据这个状态转移方程,我们可以填充好整个表格,如图所示:
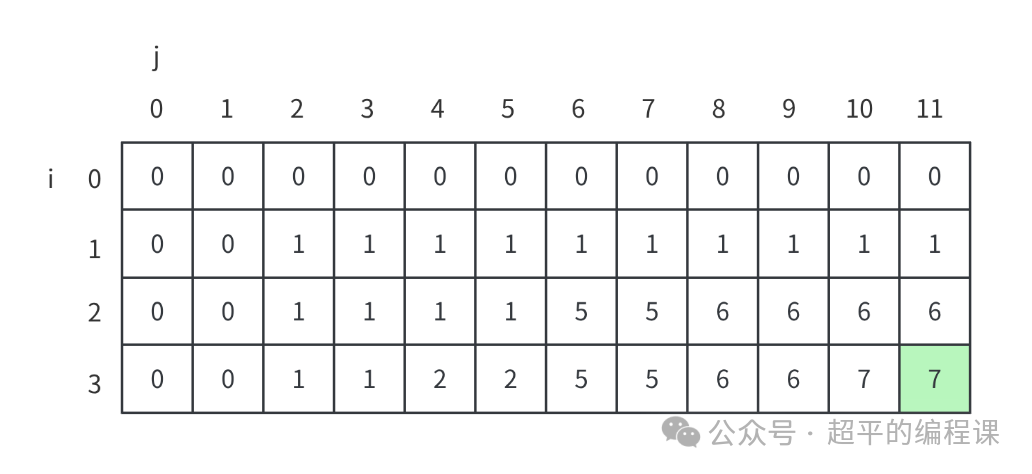
最右下角的dp[3][11] = 7,就是最大价值了。
4). 遍历顺序
通过上面的分析,可以发现,在计算dp[i][j]时,需要考虑正上方和左上方的单元格,所以我们按照从上到下,从左到右的顺序,如图:
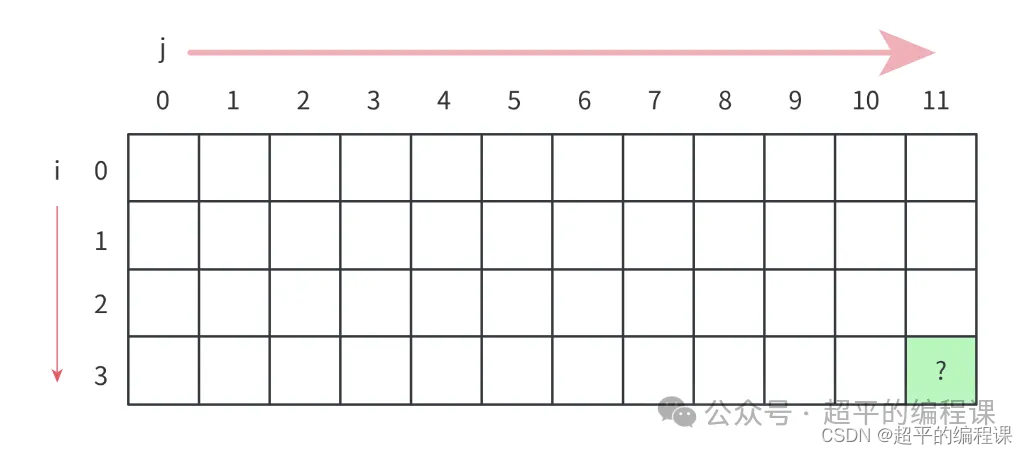
如此一来,咱们的4个核心要素都一一解决了。
思路有了,接下来,我们就进入具体的编程实现环节。
三.编程实现
根据上面的思路分析,我们使用两种方法来编写程序:
-
枚举算法
-
动态规划
1. 递归算法
根据前面的思路分析,我们编写代码如下:
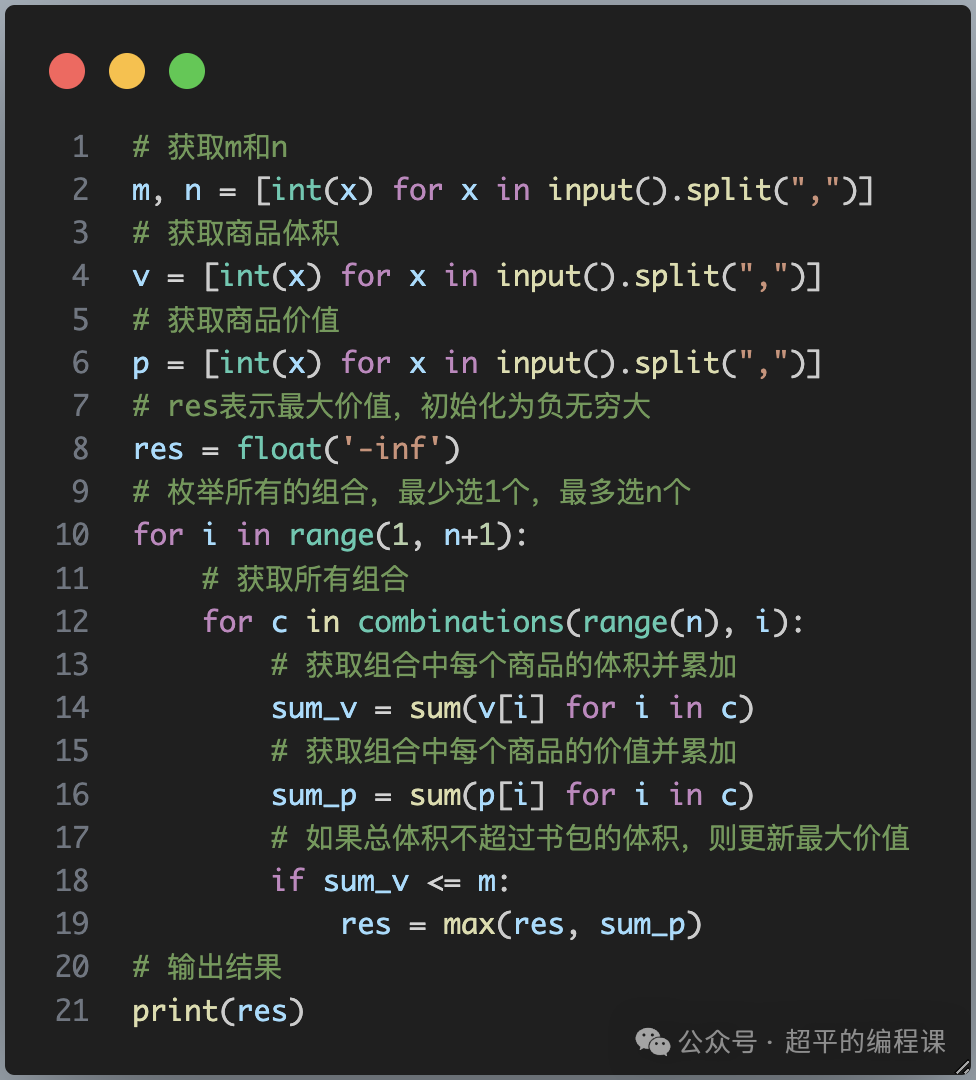
代码不多,说明两点:
1). 在获取m和n的时候,先使用了列表推导式,得到列表,然后使用解包赋值运算对m和n赋值;
2). 在计算体积和和商品和时,使用了列表推导式,得到一个列表,然后直接使用sum()函数求和,代码非常简洁;
2. 动态规划
根据前面的思路分析,编写代码如下:
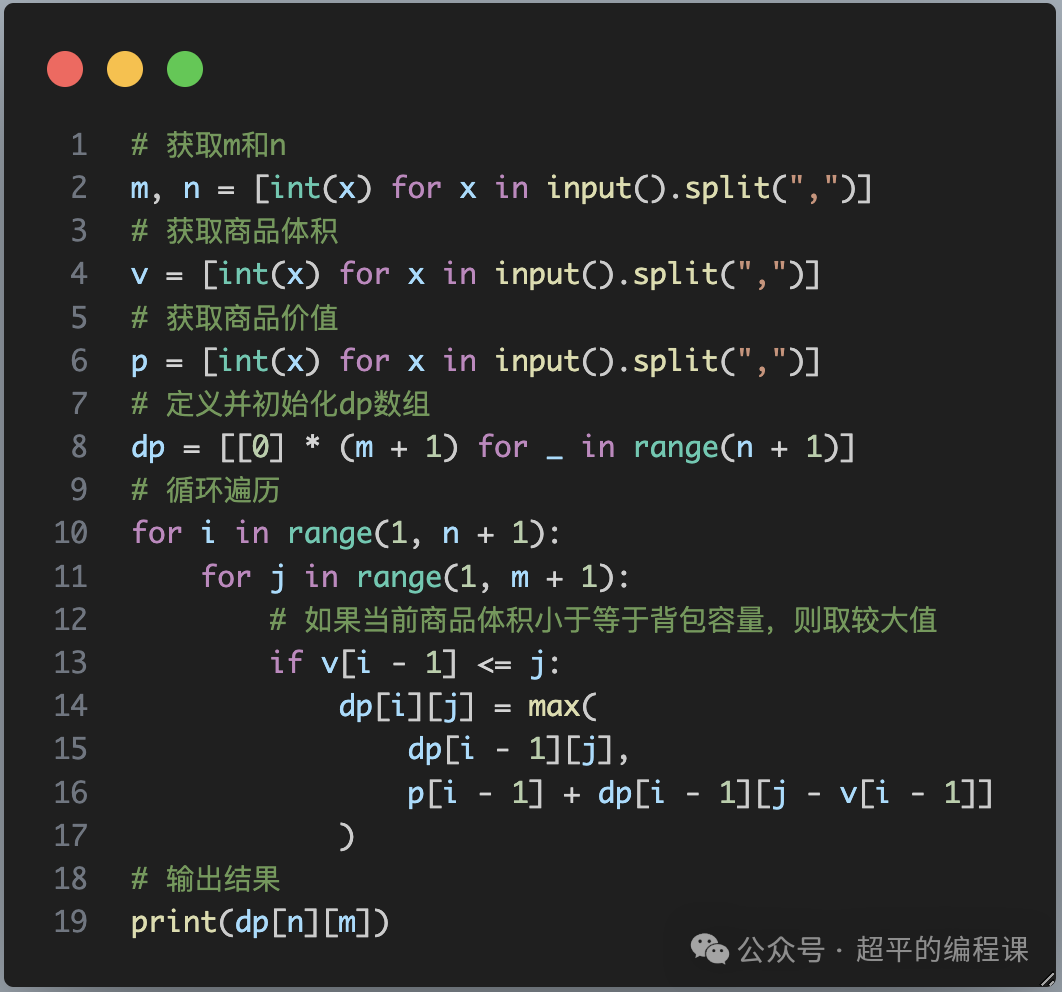
代码其实不多,说明三点:
1). 在定义dp二维数组的时候,结合了快速创建列表和列表推导式的编程技巧,此处的下划线_是一个变量名;
2). dp二维数组增加了i = 0的行和j = 0的列,实际计算是从dp[1][1]开始的;
3). 在获取商品i的体积和价值时,需要将i减去1,因为v和p两个列表的下标都是从0开始的。
至此,整个程序就全部完成了,你可以输入不同的数据来测试效果啦。
四.总结与思考
本题代码在12行左右,涉及到的知识点包括:
-
循环语句;
-
列表操作;
-
枚举算法;
-
动态规划算法;
-
01背包问题;
作为本次测评的最后一题,虽然代码不多,但是难度较大。关键点是熟练掌握动态规划算法的思想和分析方法。
01背包是经典的动态规划问题,具体来说,它属于线性DP,其特点是每个状态通常只与前一个或几个状态相关,因此可以使用一维或二维数组来存储和计算状态。
解决线性DP问题的一般步骤包括定义状态、确定状态转移方程、设定初始条件和确定遍历顺序,然后通过循环计算最优解,从而求解问题。
理解动态规划算法最好的方法就是画出表格,一步一步分析,千万不要纠结于代码本身,一般来说,动态规划的代码都比较简短,写起来也很快。
超平老师给你留一道思考题,本题可以使用递归方法来实现吗,代码如何编写呢?
你还有什么好的想法和创意吗,也非常欢迎和超平老师分享探讨。
如果你觉得文章对你有帮助,别忘了点赞和转发,予人玫瑰,手有余香😄
需要源码的,可以移步至“超平的编程课”gzh。
这篇关于商品最大价值-第13届蓝桥杯选拔赛Python真题精选的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





