VUE3 学习笔记（12）：对比Vuex与Pinia状态管理的基本理解

本文主要是介绍VUE3 学习笔记（12）：对比Vuex与Pinia状态管理的基本理解，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

在组件传值中，当嵌套关系越来越复杂的时候必然会将混乱，是否可以把一些值存在一个公共位置，无须传值直接调用呢？VUEX应运而生，但是从VUE3开始对VUEX的支持就不那么高了，官方推荐使用Pinia。

Vuex配置

ST1:安装vuex

npm install --save vuex

或者

Cnpm install --save vuex

ST2:创建JS文件

目录/src/vuex(创建目录)

目录/src/vuex/index.js

import {createStore} from "vuex";
export default createStore({state:{num:100}
})

入口文件（main.js）

import './assets/main.css'import { createApp } from 'vue'
import App from './App.vue'
import router from './router'
import store from './vuex'const app = createApp(App)app.use(router,store)app.mount('#app')

ST3:使用数据

<template><nav><h3>{{ store.state.num }}</h3></nav><RouterView />
</template>
<script >import store from "@/vuex/index.js";export default {computed: {//第一种获取方法store() {return store}}}</script>

可能因为版本的原因，我使用...mapState(["num"])，然后页面<h3>{{num}}</h3>显示报错，这种方法理论上也是可行的，但没有成功。

新项目中创建Pinia

截止到文章发表日，官方还是推荐放弃vuex,推荐使用Pinia，可以理解Pinia是最新版的VUEX

项目创建选项

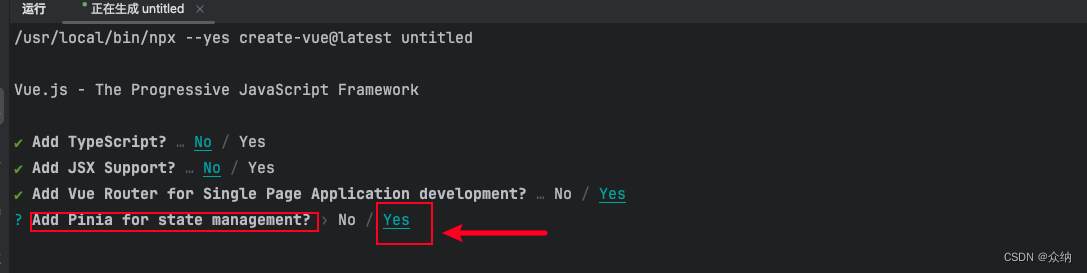
理解Pinia的核心js

自带的是组合式API，我在下面的JS代码中做了注释，请细看

位置：目录/src/stores/counter.js

import { ref, computed } from 'vue'
import { defineStore } from 'pinia'export const useCounterStore= defineStore('counter', () => {//ref 相当于state 相当于data定义const count = ref(5)const name = ref('test')//计算属性 相当于gettersconst doubleCount = computed(() => count.value * 2)//相当于methods 相当于actionfunction increment() {count.value++}function changeName(newName) {name.value = newName
}//最后把它作为一个对象暴露出去return { count,name, doubleCount, increment,changeName }
})

使用与传值

<template><h3>{{ user.doubleCount }}</h3><div><button @click="user.increment">{{ user.name }} count is: {{ user.count }}</button></div><div><button @click="user.changeName('张三')">修改名称</button></div>
</template>
<script setup>
import { RouterLink, RouterView } from 'vue-router'
import HelloWorld from './components/HelloWorld.vue'
import {useCounterStore} from "@/stores/counter.js";
const user = useCounterStore();
</script>