堆栈实现四则运算

本文主要是介绍堆栈实现四则运算，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

要实现四则运算求值，存在一个很明显的问题，就是计算机的计算不会像人类一样按优先级进行计算，因此你需要通过设置两个栈进行计算优先级的设定。一个是数值的栈，一个是字符的栈。

1. 前中后缀表达式的转换

自然表达式转换为前/中/后缀表达式，其实是很简单的。首先将自然表达式按照优先级顺序，构造出与表达式相对应的二叉树，然后对二叉树进行前/中/后缀遍历，即得到前/中/后缀表达式。
举例说明将自然表达式转换成二叉树：
$a×(b+c)-d$
① 根据表达式的优先级顺序，首先计算 $(b+c)$ ，形成二叉树
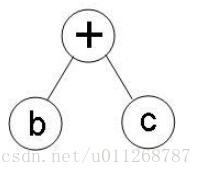
这里写图片描述
②然后是 $a×(b+c)$ ，在写时注意左右的位置关系

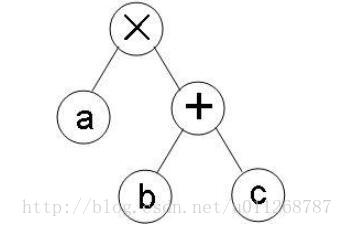
③最后在右边加上 $-d$

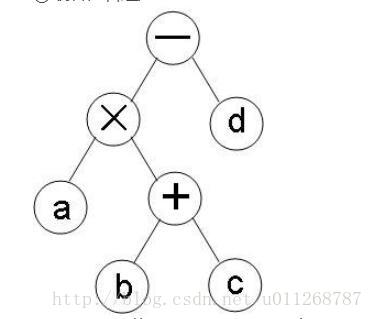
然后最这个构造好的二叉树进行遍历，三种遍历的顺序分别是这样的：
① 前序遍历：根-左-右
② 中序遍历：左-根-右
③ 后序遍历：左-右-根
所以还是以刚才的这个例子，在最终二叉树的基础上可以得出：
前缀表达式： $-*a+bcd$
中缀表达式： $a*b+c-d$

2.中缀表达式转后缀表达式（栈的应用)

中缀表达式 $9+（3-1）*3+10/2$ 转化为后缀表达式为 $9 3 1- 3 * + 10 2 / +$ .
规则：从左到右遍历中缀表达式的每一数字和符号，若是数字就输出，即成为后缀表达式的一部分；若是符号，则判断其与栈顶符号的优先级，是右括号或优先级低于栈顶符号（乘除优先加减）则栈顶元素依次出栈并输出，并将当前符号进栈，一直到最终输出后缀表达式为止。

a.初始化一空栈，用来对符号进出栈使用。b.第一个字符是数字9，输出9，后面是符号“+”，进栈。c.第三个字符是“（”，依然是符号，因其只是左括号，还没有配对，故进栈。d.第四个字符是数字3，输出，总表达式为9 3，接着是“-”，进栈。e.接下来是数字1，输出，总表达式为9 3 1，后面是符号“）”，此时，我们需要去匹配此前的“（”，所以栈顶依次出栈，并输出，直到“（”出栈为止。此时左括号上方只有“-”，因此输出“-”。总的表达式为9 3 1 -。f.接着是数字3，输出，总的表达式为9 3 1 - 3.紧接着是符号“*”，因为此时的栈顶符号为“+”号，优先级低于“*”，因此不输出，“*”进栈。g.之后是符号“+”，此时当前栈顶元素“*”比这个“+”的优先级高，因此栈中元素出栈并输出（没有比“+”更低的优先级，所以全部出栈），总输出表达式为9 3 1 - 3 * +。然后将当前这个符号“+”进栈。h.紧接着数字10，输出，总表达式为9 3 1 - 3 * + 10。后是符号“/”，所以“/”进栈。i.最后一个数字2，输出，总的表达式为9 3 1 - 3 * + 10 2。j.因已经到最后，所以将栈中符号全部出栈并输出。最终输出的后缀表达式结果为9 3 1 - 3 * + 10 2 / +。

3.后缀表达式计算结果（栈的应用）

后缀表达式为： $9 3 1 - 3 * + 10 2 / +$

规则为：从左到右遍历表达式的每个数字和符号，遇到是数字就进栈，遇到是符号，就将处于栈顶两个数字出栈，进行运算，运算结果进栈，一直到最终获得结果。

a.初始化一个空栈。此栈用来对要运算的数字进行进出使用。

b.后缀表达式中前三个是、都是数字，所以9 3 1 进栈。

c.接下来是“-”，所以将栈中的1出栈作为减数，3出栈作为被减数，并运算3-1得到2，再讲2进栈。

d.接着是数字3进栈。

e.后面是“*”，也就意味着栈中3和2出栈，2与3相乘，得到6，并将6进栈。

f.下面是“+”，所以栈中6和9出栈，9和6相加，得到15，将15进栈。

g.接着是10和2两数字进栈。

h.接下来是符号“/”，因此，栈顶的2与10出栈，10与2相除，得到5，将5进栈。

i.最后一个是符号“+”，所以15与5出栈并相加，得到20，讲20进栈。

j.结果是20出栈，栈变为空。

代码：

//下面的代码只是支持一些简单的整数的加减乘除运算，而且不支持浮点数，负数或者数字大于9的数字的运算，只是  
//自己简单的写一个代码，将这个过程进行的简单验证，如果需要解决复杂的计算问题，可以上网查找资料来实现！   
#include<iostream>  
#include<cstdio>  
#include<string>  
#include<stack>  
using namespace std;  stack<char> s;   
stack<int> ss;   int main()  
{  int len1, len2, len, i, j;  string str1, str2;//str1为中缀表达式，str2为后缀表达式   while (1){  //中缀表达式转换为后缀表达式   getline(cin, str1);  len1 = str1.length();  str2.clear();   for (i = 0; i < len1; i++){  if (str1[i] >= '0' && str1[i] <= '9')   str2.push_back(str1[i]);  else{  if (s.size() == 0 || str1[i] == '(')  s.push(str1[i]);  else{  char tmp1 = s.top();  if (str1[i] == ')'){  len = s.size();   while (len){  char tmp = s.top();   s.pop();  if (tmp == '(')  break;  else   str2.push_back(tmp);   len--;   }   }   else{  if (tmp1 == '*' || tmp1 == '/'){  if (str1[i] == '*' || str1[i] == '/')   s.push(str1[i]);  else{  len = s.size();   while (len){  char tmp = s.top();   str2.push_back(tmp);  s.pop();   len--;   }  s.push(str1[i]);    }   }   else{  s.push(str1[i]);   }   }   }    }   }  if (s.size() != 0){  len = s.size();   while (len){  char tmp = s.top();   str2.push_back(tmp);  s.pop();   len--;   }   }   cout << str2 << endl;  //由后缀表达式计算结果   int temp1, temp2, temp3;   len2 = str2.length();  for (i = 0; i < len2; i++){  if (str2[i] >= '0' && str2[i] <= '9'){   int t = str2[i]-48;   ss.push(t);   }   else{  temp1 = ss.top();  ss.pop();  temp2 = ss.top();  ss.pop();   if (str2[i] == '+'){  temp3 = temp2 + temp1;   }  else if (str2[i] == '-'){  temp3 = temp2 - temp1;   }  else if (str2[i] == '*'){  temp3 = temp2 * temp1;   }  else if (str2[i] == '/'){  temp3 = temp2 / temp1;   }  ss.push(temp3);   }  }  cout << ss.top() << endl;   }   system("pause");  
}