【LeetCode刷题】二分查找：寻找旋转排序数组中的最小值、点名

本文主要是介绍【LeetCode刷题】二分查找：寻找旋转排序数组中的最小值、点名，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

【LeetCode刷题】Day 14

题目1：153.寻找旋转排序数组中的最小值
- 思路分析：
- 思路1：二分查找：以A为参照
- 思路2：二分查找，以D为参照
题目2：LCR 173.点名
- 思路分析：
- 思路1：遍历查找
- 思路2：哈希表
- 思路3：异或
- 思路4：求和
- 思路5：二分查找

在这里插入图片描述

题目1：153.寻找旋转排序数组中的最小值

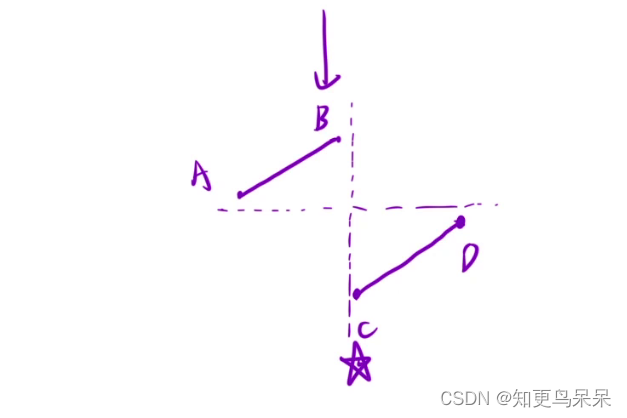
在这里插入图片描述

思路分析：

在这里插入图片描述

O(logN)来做，我们就直接二分查找。所以第一步，去寻找其中的二段性。
这里我们可以有两种方式：以A为参照，以D为参照，来找C点的值。

思路1：二分查找：以A为参照

以A为参照：

1. 二段性：[A-B段都大于等于A][C-D段都小于A]

2. 迭代：C点在left外，所以left=mid+1，C在right内，所以right=mid，没有-1上面就不用+1，mid=left+(right-left)/2

特殊情况：翻转后刚好是原来的升序数组，此时以A为参照会把该数组当成全部A-B段，会不断向外找，直到left<right不成立而结束，该情况需要特殊处理。

代码实现：

class Solution {
public:int findMin(vector<int>& nums) {int left=0,right=nums.size()-1;if(nums[left]<nums[right]) return nums[left];while(left<right){int mid=left+(right-left)/2;if(nums[mid]>=nums[0]) left=mid+1;else right=mid;}return nums[right];}
};

思路2：二分查找，以D为参照

以C为参照：

1. 二段性：[A-B段都大于D][C-D段都小于等于D]

2. 迭代：C点在left外，所以left=mid+1，C在right内，所以right=mid，没有-1上面就不用+1，mid=left+(right-left)/2

无特殊情况：若翻转后刚好是原来的升序数组，会把整个数组当成C-D段，以D为参照，会往下找，就可以找到C，所以无需处理

代码实现：

class Solution {
public:int findMin(vector<int>& nums) {int left=0,right=nums.size()-1; while(left<right){int mid=left+(right-left)/2;if(nums[mid]>nums[nums.size()-1]) left=mid+1;else right=mid;}return nums[right];}
};

LeetCode链接：153.寻找旋转排序数组中的最小值

题目2：LCR 173.点名

在这里插入图片描述

思路分析：

这道题很简单，有很多思路，简单的我就直接讲一下过程就OK。

思路1：遍历查找

遍历数组，寻找后一位减前一位的差为2的数，找到就返回，没找到就返回最后一个数的下一个。

思路2：哈希表

分别将数据导入哈希表，然后查看哪个数的个数为零，返回该值。

思路3：异或

数组records[0]~records[size-1] 与当前数组各个数异或，若结果为x，则返回x；当x等于0时，需要格外处理，有两种情况，缺0或者是最后一个数后面的数。需要特殊处理：比对第一个数是不是0就可以。

思路4：求和

数组records[0]~records[size-1] 的和减去当前数组的和。若结果为x，则返回x；当x等于0时，需要格外处理，与思路3一样。

思路5：二分查找

这道题的二分查找很有趣，需要细节，能发现二段性，这题就相当简单。我们可以发现这个升序数组是从0到n-1，所以我们可以发现这样一个
二段性：[缺失值前面，下标与值相同][缺失值后面，下标与值不同]，我们找到右区间的左值的下标就是缺失的值。
细节处理：当所有数的值和下标相同时，则返回left+1.

代码实现：

class Solution {
public:int takeAttendance(vector<int>& records) {int left=0,right=records.size()-1;while(left<right){int mid=left+(right-left)/2;if(mid==records[mid]) left=mid+1;else right=mid;}//处理细节：如果缺失的是最后一位if(left==records[left]) return left+1;else return left;}
};