本文主要是介绍Codeforces Round 548 (Div. 2) C. Edgy Trees,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
Edgy Trees
You are given a tree (a connected undirected graph without cycles) of n n n vertices. Each of the n − 1 n - 1 n−1 edges of the tree is colored in either black or red.
You are also given an integer k k k. Consider sequences of k k k vertices. Let’s call a sequence [ a 1 , a 2 , … , a k ] [a_1, a_2, \ldots, a_k] [a1,a2,…,ak] good if it satisfies the following criterion:
- We will walk a path (possibly visiting same edge/vertex multiple times) on the tree, starting from a 1 a_1 a1 and ending at a k a_k ak.
- Start at a 1 a_1 a1, then go to a 2 a_2 a2 using the shortest path between a 1 a_1 a1 and a 2 a_2 a2, then go to a 3 a_3 a3 in a similar way, and so on, until you travel the shortest path between a k − 1 a_{k-1} ak−1 and a k a_k ak.
- If you walked over at least one black edge during this process, then the sequence is good.
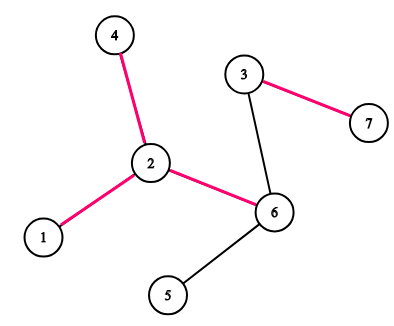
Consider the tree on the picture. If k = 3 k=3 k=3 then the following sequences are good: [ 1 , 4 , 7 ] [1, 4, 7] [1,4,7], [ 5 , 5 , 3 ] [5, 5, 3] [5,5,3] and [ 2 , 3 , 7 ] [2, 3, 7] [2,3,7]. The following sequences are not good: [ 1 , 4 , 6 ] [1, 4, 6] [1,4,6], [ 5 , 5 , 5 ] [5, 5, 5] [5,5,5], [ 3 , 7 , 3 ] [3, 7, 3] [3,7,3].
There are n k n^k nk sequences of vertices, count how many of them are good. Since this number can be quite large, print it modulo 1 0 9 + 7 10^9+7 109+7.
Input
The first line contains two integers n n n and k k k ( 2 ≤ n ≤ 1 0 5 2 \le n \le 10^5 2≤n≤105, 2 ≤ k ≤ 100 2 \le k \le 100 2≤k≤100), the size of the tree and the length of the vertex sequence.
Each of the next n − 1 n - 1 n−1 lines contains three integers u i u_i ui, v i v_i vi and x i x_i xi ( 1 ≤ u i , v i ≤ n 1 \le u_i, v_i \le n 1≤ui,vi≤n, x i ∈ { 0 , 1 } x_i \in \{0, 1\} xi∈{0,1}), where u i u_i ui and v i v_i vi denote the endpoints of the corresponding edge and x i x_i xi is the color of this edge ( 0 0 0 denotes red edge and 1 1 1 denotes black edge).
Output
Print the number of good sequences modulo 1 0 9 + 7 10^9 + 7 109+7.
Example
| i n p u t \tt input input |
|---|
| 4 4 1 2 1 2 3 1 3 4 1 |
| o u t p u t \tt output output |
| 252 |
| i n p u t \tt input input |
|---|
| 4 6 1 2 0 1 3 0 1 4 0 |
| o u t p u t \tt output output |
| 0 |
| i n p u t \tt input input |
|---|
| 3 5 1 2 1 2 3 0 |
| o u t p u t \tt output output |
| 210 |
Note
In the first example, all sequences ( 4 4 4^4 44) of length 4 4 4 except the following are good:
- [ 1 , 1 , 1 , 1 ] [1, 1, 1, 1] [1,1,1,1]
- [ 2 , 2 , 2 , 2 ] [2, 2, 2, 2] [2,2,2,2]
- [ 3 , 3 , 3 , 3 ] [3, 3, 3, 3] [3,3,3,3]
- [ 4 , 4 , 4 , 4 ] [4, 4, 4, 4] [4,4,4,4]
In the second example, all edges are red, hence there aren’t any good sequences.
Tutorial
由于题目要求中有至少走过一条黑边,所以我们可以用正难则反的思想,求出所有坏序列,即一条黑边也没有,最后再用所有序列减去坏序列即为结果
首先我们可以将黑边删除,剩下的都将是红边连接的分块,对于每个分块,它们自身元素的连接均为坏序列,序列个数为 s z k sz^k szk,其中 z s zs zs 为当前分块的节点个数,此时想要建成好序列就需要与其他分块相连,即通过一条黑边
由于所有的序列个数为 n k n^k nk,所以最终答案为 n k − ∑ z s k n^k - \sum zs^k nk−∑zsk,其中 s z sz sz 为当前分块的节点个数
此解法时间复杂度为 O ( α ( n ) ) \mathcal O(\alpha(n)) O(α(n)),即并查集的时间复杂度
Solution
#include <bits/stdc++.h>
using namespace std;#define endl '\n'
#define int long long
const int mod = 1e9 + 7; // 998244353;struct DSU { // 并查集vector<int> pre, siz;DSU() {}DSU(int n) {pre.resize(n + 1);std::iota(pre.begin(), pre.end(), 0);siz.assign(n + 1, 1);}int find(int x) {if (pre[x] == x) {return x;}return pre[x] = find(pre[x]);}bool same(int x, int y) {return find(x) == find(y);}bool merge(int x, int y) {x = find(x);y = find(y);if (x == y) {return false;}siz[x] += siz[y];pre[y] = x;return true;}int size(int x) {return siz[find(x)];}
};int ksm(int x, int y, int mod) {x %= mod;int ans = 1;while (y) {if (y & 1) {ans = (ans * x) % mod;}x = (x * x) % mod;y >>= 1;}return ans;
}signed main() {int n, k;cin >> n >> k;int ans = ksm(n, k, mod);DSU dsu(n);vector<int> memo(n + 1);for (int i = 1; i < n; ++i) {int u, v, x;cin >> u >> v >> x;if (not x) {dsu.merge(u, v);}}for (int i = 1; i <= n; ++i) {if (not memo[dsu.find(i)]) {ans -= ksm(dsu.size(i), k, mod);ans = (ans + mod) % mod;memo[dsu.find(i)] = 1;}}cout << ans << endl;return 0;
}
这篇关于Codeforces Round 548 (Div. 2) C. Edgy Trees的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






