本文主要是介绍Mathematica画图系列 做了该用geogebra做的事情。。,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
群里看到这样一张图,就顺手画了
代码如下:
Manipulate[Block[{r1 = 5, o},Graphics[{Circle[{0, 0}, 5],Circle[(r1 - r2) {Cos[t], Sin[t]}, r2],Gray, l = Table[o = (r1 - r2) {Cos[i], Sin[i]};Line@{o, o + k r2 {Cos[i*r1/r2], Sin[-i*r1/r2]}}, {i, 0, t, Pi/96.}],Black, Thick, Line@l[[;; , 1, 2]]}]], {t, 0, 2 Pi}, {r2, 0.1, 5}, {k, 1, 2}]

需要思路和过程的话继续往下看~
首先,仿照原图那样,画两个圆,至于半径完全是看心情的
Block[{r1 = 5, r2 = 2, t = 0},Graphics[{Circle[{0, 0}, 5],Circle[{(r1 - r2) Cos[t], (r1 - r2) Sin[t]}, r2]}]]
然后,套一层Manipulate让他们动起来
Manipulate[Block[{r1 = 5, r2 = 2},Graphics[{Circle[{0, 0}, 5],Circle[{(r1 - r2) Cos[t], (r1 - r2) Sin[t]}, r2]}]], {t, 0, 2 Pi}]
下一步就开始画线了,这一步发现小圆的圆心坐标多次用到,于是设个变量,减小代码量也可以提高运行效率
Manipulate[Block[{r1 = 5, r2 = 2, o},o = (r1 - r2) {Cos[t], Sin[t]};Graphics[{Circle[{0, 0}, 5],Circle[o, r2],Line@{o, o + 1.2 r2 {Cos[t*r1/r2], Sin[-t*r1/r2]}}}]], {t, 0, 2 Pi}]
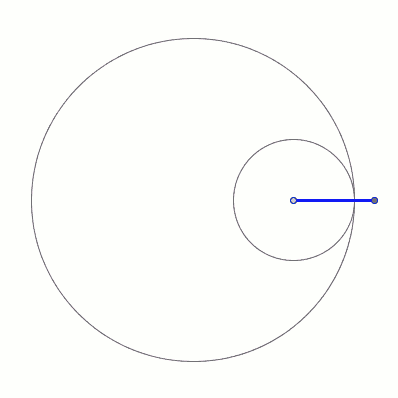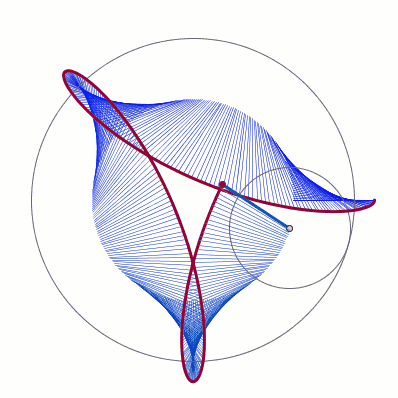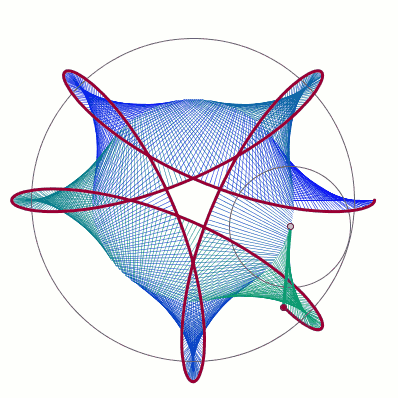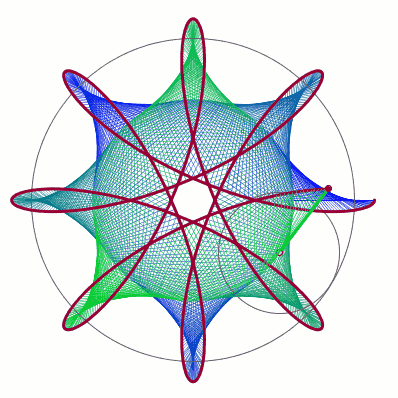
下一步,把线段扫过的区域画出来,用Table生成即可
Manipulate[Block[{r1 = 5, r2 = 2, o},o = (r1 - r2) {Cos[t], Sin[t]};Graphics[{Circle[{0, 0}, 5],Circle[o, r2],Table[o = (r1 - r2) {Cos[i], Sin[i]};Line@{o, o + 1.2 r2 {Cos[i*r1/r2], Sin[-i*r1/r2]}}, {i, 0, t, Pi/96.}]}]], {t, 0, 2 Pi}]
然后,再加上其他可以调节的参数
Manipulate[Block[{r1 = 5, o},Graphics[{Circle[{0, 0}, 5],Circle[(r1 - r2) {Cos[t], Sin[t]}, r2],Table[o = (r1 - r2) {Cos[i], Sin[i]};Line@{o, o + k r2 {Cos[i*r1/r2], Sin[-i*r1/r2]}}, {i, 0, t, Pi/96.}]}]], {t, 0, 2 Pi}, {r2, 0.1, 5}, {k, 1, 2}]
最后,把另一端的轨迹画出来,然后适当更改图形的样式,美(丑?)化一下
就是最后的代码了(和文章开头的略有不同哦,使用函数避免了很多次书写{Cos[t],Sin[t]}这种东西
Manipulate[Block[{r1 = 5, o, c},c[x_] := {Cos[x], Sin[x]};Graphics[{Circle[{0, 0}, 5],Circle[(r1 - r2) c[t], r2],Gray, l = Table[o = (r1 - r2) c[i];Line@{o, o + k r2 c[-i*r1/r2]}, {i, 0, t, Pi/96.}],Black, Thick, Line@l[[;; , 1, 2]]}]], {t, 0, 2 Pi}, {r2, 0.1, 5}, {k, 1, 2}]
这篇关于Mathematica画图系列 做了该用geogebra做的事情。。的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!









