本文主要是介绍软件无线电学习-发射机体系结构,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
本文知识内容摘自《软件无线电原理和应用》
软件无线电主要由发射机和接收机两大部分组成。软件无线电发射机的主要功能是把需发射或传输的用户信息(话音、数据或图像)经基带处理(完成诸如FM、AM、FSK、PSK、MSK、QAM 等调制)和上变频,调制到规定的载频(中心频率)上,再通过功率放大后送至天线,把电信号转换为空间传播的无线电信号,发向空中或经传输介质(如电缆、光缆)送到接收方的接收机前端,由其进行接收解调。其过程如下图所示。

如前所示,任何一个无线电信号均可以表示为:
式中,a(t)和分别表示该信号的幅度调制信息和相位调制信息,
为信号载频(中心频率),而频率调制信息也反映在相位调制信息中,即:
对上述式子进行数字化
其中,为采样间隔,上式子简写为:
式中,为数字角频率,取0-
(实信号),有时不加区分地把
和
都称为角频率,只要记住在信号表达式中的真正含义就是了。为了便于信息调制,通常把上式进行正交分解:
其中和
调制的方式是现求出I(n)和Q(n)然后分别与两个正交本振和
相乘并求和,即可得到调制信号s(n)
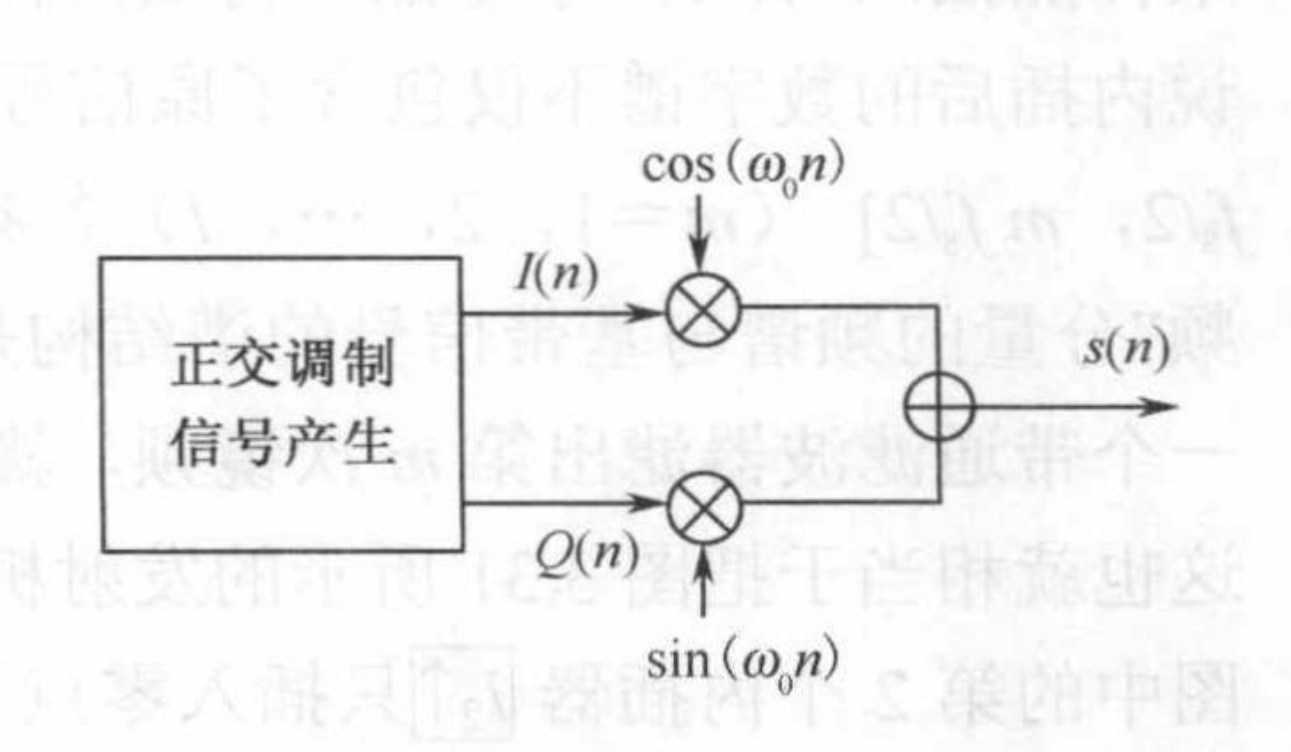
matlab仿真程序。
clc;
clear;
% 设置参数
fs = 5e9; % 采样率 5GHz
fc = 50e6; % 基带频率
fm = 100e6; % NCO信号频率t = 0:1/fs:1e-3; % 时间序列,1微秒% 基带信号
i = cos(2*pi*fc*t);%余弦波
q = -sin(2*pi*fc*t);%正弦波% nco本振信号
i_nco = cos(2*pi*fm*t);
q_nco = sin(2*pi*fm*t);% iq调制
iq = i.*i_nco + q.*q_nco;% 绘制频域波形% 计算频谱
N = length(t);
f = (-fs/2:fs/N:fs/2-fs/N); % 频率向量
I = fftshift(fft(i));
Q = fftshift(fft(q));
I_NCO = fftshift(fft(i_nco));
Q_NCO = fftshift(fft(q_nco));
IQ= fftshift(fft(iq));
figure(1);
subplot(4,1,1);
plot(f, abs(I)/N,'b');
title('基带I频谱');
xlabel('频率 (GHz)');
ylabel('幅度');subplot(4,1,2);
plot(f, abs(Q)/N,'b');
title('基带Q频谱');
xlabel('频率 (GHz)');
ylabel('幅度');subplot(4,1,3);
plot(f, abs(I_NCO)/N,'g');
title('i_nco本振信号频谱');
xlabel('频率 (GHz)');
ylabel('幅度');subplot(4,1,4);
plot(f, abs(Q_NCO)/N,'r');
title('q_nco本振信号频谱');
xlabel('频率 (GHz)');
ylabel('幅度');figure(2);
plot(f, abs(IQ)/N,'b');
title('iq调制频谱');
xlabel('频率 (GHz)');
ylabel('幅度');
设置采样率为5ghz,基带信号为50mhz,nco本振为100mhz,第一步先求出基带信号的IQ信号,在求出正交本振cos和sin。相乘后相加。
实验现象如下如所示。
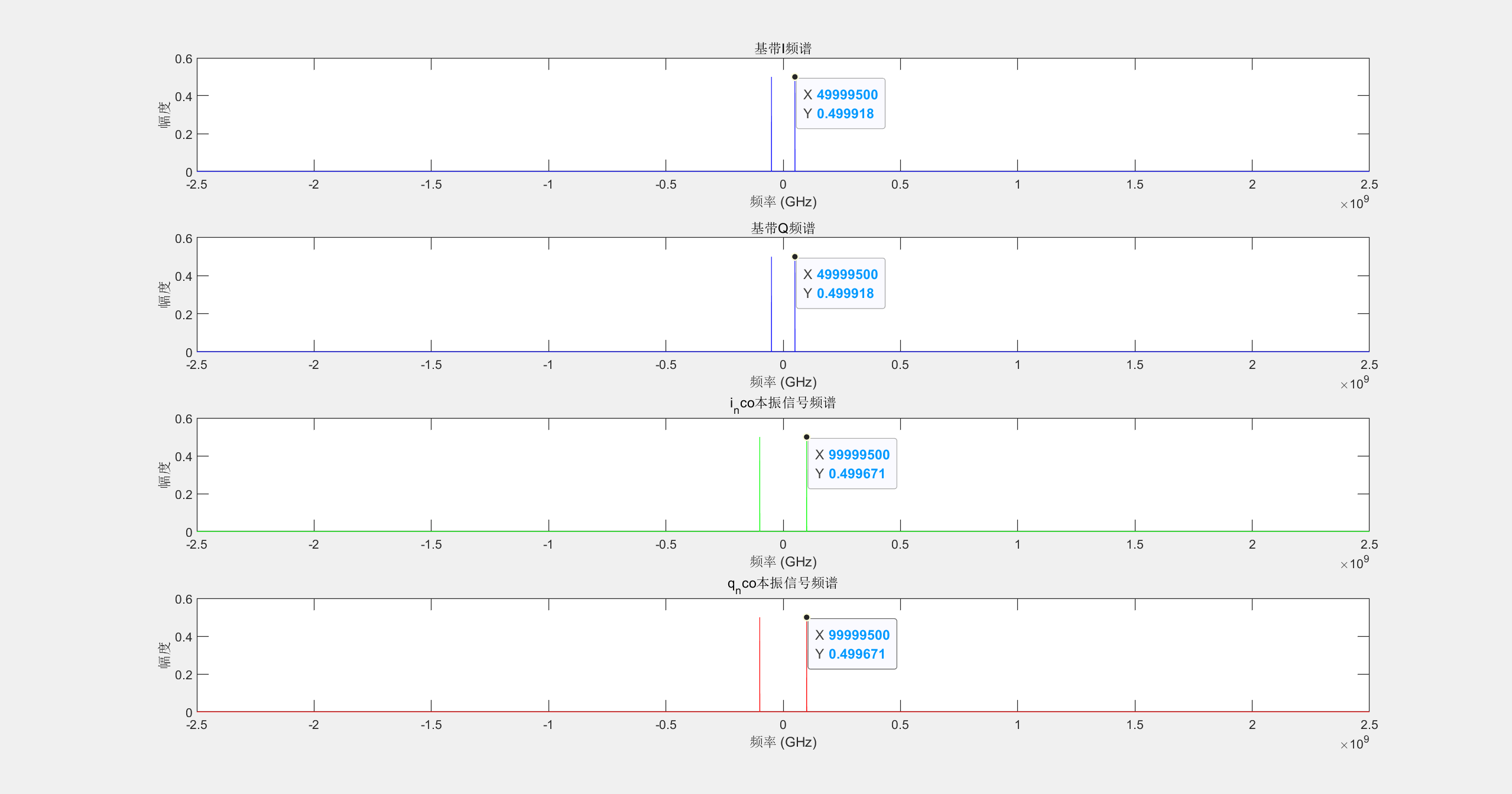
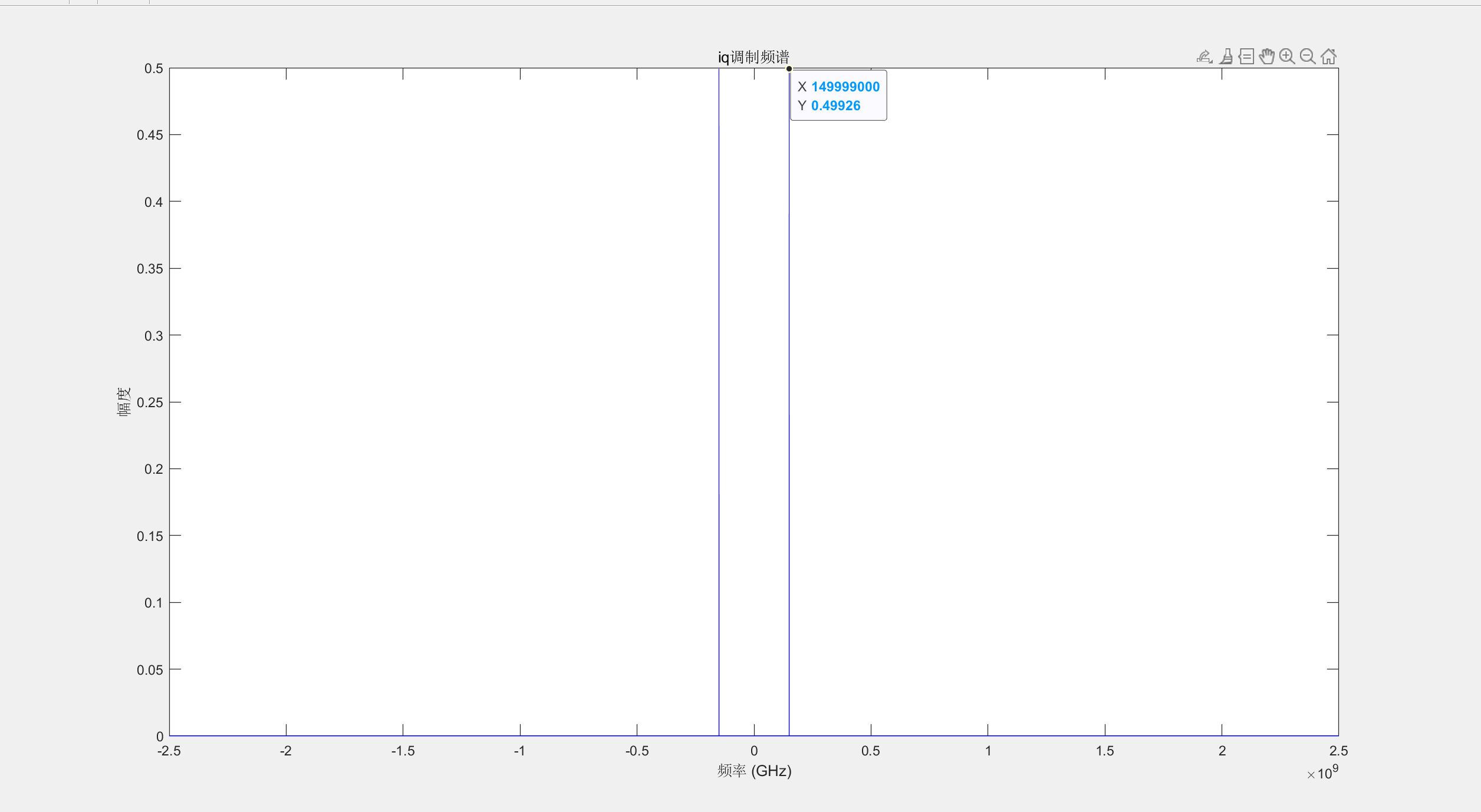
这篇关于软件无线电学习-发射机体系结构的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







