本文主要是介绍【NOIP2013模拟】Freda的传呼机 题解+代码,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
这题又有点像码农题!!
Description
为了 随时 与 rainbow快速交流, Freda制造了 两部传呼机 。Freda和 rainbow所在的地方有N座房屋、M条双向 光缆 。每条光缆连接两座房屋, 传呼机发出的信号只能沿着光缆传递,并且 传呼机的信号 从光缆的其中一端传递到另需要花费 t单位时间 。现在 Freda要 进行 Q次试验, 每次选取两座房屋,并想知道 传呼机的信号在这两座房屋之间传递 至少需 要多长时间。 Freda 和 rainbow简直弱爆了有木有T_TT_T ,请你帮他们吧……
N座房屋 通过光缆 一定是连通的, 并且这 M条光缆有以下三类连接情况:
A:光缆不形成环 ,也就是光缆仅 有 N-1条。
B:光缆只 形成一个环,也就是光缆 仅有 N条。
C:每条光缆仅在一个环中。
Input
第一行 包含三个用空格隔开的整数, N、M和 Q。
接下来 M行每三个整数 x、y、t,表示 房屋 x和 y之间有一条传递时为 t的光缆 。
最后 Q行每两个整数 x、y,表示 Freda想知道 在 x和 y之间传呼最少需要多长时间。
Output
输出 Q行,每一个整数表示 Freda每次试验的结果 。
Sample Input
输入1:
5 4 2
1 2 1
1 3 1
2 4 1
2 5 1
3 5
2 1
输入2:
5 5 2
1 2 1
2 1 1
1 3 1
2 4 1
2 5 1
3 5
2 1
输入3:
9 10 2
1 2 1
1 4 1
3 4 1
2 3 1
3 7 1
7 8 2
7 9 2
1 5 3
1 6 4
5 6 1
1 9
5 7
Sample Output
输出1:
3
1
输出2:
3
1
输出3:
5
6
Data Constraint
送分数据占10%,2<=N<=1000,N-1<=M<=1200。
A类数据占30%,M=N-1。
B类数据占50%,M=N。
C类数据占10%,M>N。
对于100%的数据,2<=N<=10000,N-1<=M<=12000,Q=10000,1<=x,y<=N,1<=t<=32768。
Solution
这道题可以分为四个部分讨论
P.S 如果你想AC,不用看前三部分。
第一部分:10分送分:spfa直接过
第二部分:A类数据即一颗树:用倍增LCA轻松过掉。
第三部分:B类数据即环套树
在打完第二部分分以后,一定要思考一下,这类数据是可以转换为第二类的。整整50分啊!
首先,找到这唯一的一个环,接着在这个环上随便删掉一条边,那么就变成了第二部分。可以按照第二部分一样求解。但是,也许走这条多出来的边能更短,那么何乐而不为呢?如何为呢?可以记录下这条被删掉的边的左右端点,分别使询问的点到达这两个端点,再加上这条边的长度,就是一定会走这条边的长度,取min即可。
这样就可以90分了!
但是为了最后十分
第四部分:C类数据仙人掌。
有许许多多的环,可以按照第三部分的思路,不过稍加改变。
有个叫做环顶的东西。看下面这张图:
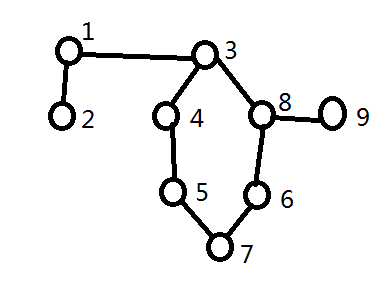
根节点是1,那么环顶就是3。可能有多个环公用一个环顶。(见最后面的数据)
怎么处理呢?
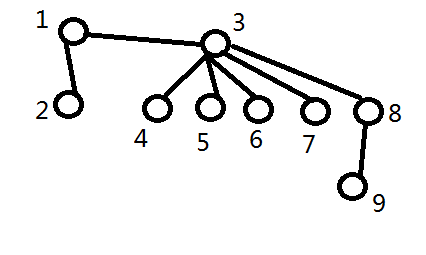
变成这样
将环中的所有点连向环顶,边的权值为它往左或往右最近的走到环顶的距离。其余的边找连,这样就转化为第一种状态了!是不是感觉可以过了?NO!
仔细思考会发现一个问题,同一个环中的点的距离不一定是走到环顶最优,有可能换个方向走更快,怎么办?把一个点到环顶的两种路,两个距离记录下来。设为f1和f2那么X和Y之间的最短路为min{ f1[x]+f2[y],f1[y]+f2[x], abs(f1[x]-f2[x])}
那么对于输入的x和y倍增到同一个环里面,然后按上面做就好了
在求环的过程中可以用Tarjan思想
完美解决
在给出代码之前,给一个数据,这个数据很全面,我就靠调这个数据调对了
输入:
13 16 4
1 2 1
2 4 1
1 3 1
3 4 4
3 12 1
12 13 1
13 3 3
3 10 1
3 11 1
10 11 1
4 6 3
4 5 1
5 6 1
6 8 1
8 7 1
8 9 1
12 13
9 13
11 4
13 11
输出:
1
9
4
3
#include<cstdio>
#include<cmath>
#include<cstring>
#include<algorithm>
#define fo(i,a,b) for(int i=a;i<=b;i++)
#define fd(i,a,b) for(int i=a;i>=b;i--)
#define N 12100
using namespace std;
int deep[N],fa[N],hzj[N],last[N*10],next[N*10],to[N*10],n,data[N*10],f[N][14],g[N][14],las2[N*10],nex2[N*10],t2[N*10],dat2[N*10],tot=1,totot=1,ttt=0,tt=0,m,ans,a[N][3],s[N][2],sy[N][4],ss=0,yj,lb[N][3],dfn[N*10],jy;
bool bz[N*10];
void putin(int x,int y,int z)
{
next[++tot]=last[x];last[x]=tot;to[tot]=y;data[tot]=z;
next[++tot]=last[y];last[y]=tot;to[tot]=x;data[tot]=z;
}
void link(int x,int y,int z)
{
nex2[++totot]=las2[x];las2[x]=totot;t2[totot]=y;dat2[totot]=z;
nex2[++totot]=las2[y];las2[y]=totot;t2[totot]=x;dat2[totot]=z;
}
void zh(int x,int y,int fa)
{
dfn[x]=++ttt;
for(int i=last[x];i;i=next[i])
{
int k=to[i];
if (k==fa && i==(y^1)) continue;
if (dfn[k]<dfn[x] && dfn[k]!=0)
{
int jy=data[i];tt++;
for(int l=ss;s[l][0]!=k;l--) jy+=s[l][1];
sy[x][0]=tt;sy[x][1]=k;sy[x][2]=data[i];sy[x][3]=jy-data[i];link(k,x,min(sy[x][2],sy[x][3]));
for(int l=ss-1;s[l][0]!=k;l--)
{
int z=s[l][0];
sy[z][0]=tt;sy[z][1]=k;sy[z][2]=sy[s[l+1][0]][2]+s[l+1][1];sy[z][3]=jy-sy[z][2];
link(k,z,min(sy[z][2],sy[z][3]));
}
continue;
}
if (dfn[to[i]]!=0) continue;
s[++ss][0]=k;s[ss][1]=data[i];zh(k,i,x);
}
ss--;
}
void dfs3(int x)
{
for(int i=las2[x];i;i=nex2[i])
{
if (t2[i]==fa[x]) continue;
fa[t2[i]]=x;hzj[t2[i]]=dat2[i];deep[t2[i]]=deep[x]+1;dfs3(t2[i]);
}
}
int lca(int x,int y)
{
int an=0;
fd(i,13,0) if (deep[f[x][i]]>=deep[y]) an+=g[x][i],x=f[x][i];
fd(i,13,0) if (deep[f[y][i]]>=deep[x]) an+=g[y][i],y=f[y][i];
fd(i,13,0) if (f[x][i]!=f[y][i]) {an=an+g[x][i]+g[y][i];x=f[x][i];y=f[y][i];}
if (x==y) return an;
if (x!=y && sy[x][0]==sy[y][0] && sy[x][0]!=0) an+=min(sy[x][2]+sy[y][3],min(sy[x][3]+sy[y][2],abs(sy[x][2]-sy[y][2])));
else an+=g[x][0]+g[y][0];
return an;
}int main()
{
int nm;
scanf("%d%d%d",&n,&m,&nm);
fo(i,1,m)
{
int x,y,z;scanf("%d%d%d",&x,&y,&z);
putin(x,y,z);lb[i][1]=x;lb[i][2]=y;lb[i][0]=z;
}
fo(i,1,nm) scanf("%d%d",&a[i][1],&a[i][2]);
ss=1;s[1][0]=1;s[1][1]=0;zh(1,-1,0);
fo(i,1,m)
{
int x=lb[i][1],y=lb[i][2],z=lb[i][0];
if ((sy[x][0]!=sy[y][0]|| sy[x][0]==0 || sy[x][0]==0) && sy[x][1]!=y && sy[y][1]!=x) link(x,y,z);
}
deep[1]=1;dfs3(1);
fo(i,1,n) f[i][0]=fa[i],g[i][0]=hzj[i];
fo(j,1,13)
fo(i,1,n)
{
f[i][j]=f[f[i][j-1]][j-1];
if (f[i][j]) g[i][j]=g[i][j-1]+g[f[i][j-1]][j-1];
}
fo(i,1,nm)
{
int x=a[i][1],y=a[i][2];
ans=lca(x,y);
printf("%d\n",ans);
}
}这篇关于【NOIP2013模拟】Freda的传呼机 题解+代码的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






