本文主要是介绍电桥的原理，及非线性误差，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
目录
误差计算
三种电桥对比
总结
误差计算
电桥电路如下：
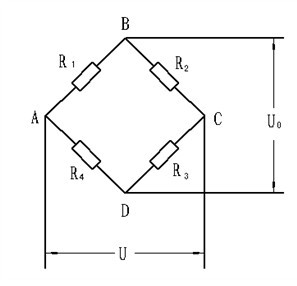
计算如下：
从上式可以看出当有激励电压时（即U≠0时），
=0的条件是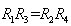
，四个电阻相等的时候是等臂电阻。当四个电阻的阻值发生变化,如桥臂上面是四个应变片，测量重力等。其输出电压的公式如下：
对上式由于
并且略去高阶项。展开公式线性化后得出如下
公式1
上面的式子是线性表达，存在非线性误差
非线性误差的计算如下：
公式2
三种电桥对比
电桥，也分为单臂电桥，半桥电路，全桥电路。
单臂电桥，如，只有R1为应变片
根据公式1，只有R1发生变化，所以有
同时根据公式2得出，单臂电桥的非线性误差为
单臂电桥电路存在非线性误差。
半桥电路 ，如R1 和R2 为应变片（相邻的桥臂），一个受力阻值变大，另外一个变小。阻值变化相同
根据公式1 可得
同时根据公式2得出，非线性误差为
从上面可得出，半桥比单臂灵敏度高2倍，且没有非线性误差。
同理全桥电路，接入四个应变片，R`和R3 阻值变化方向相同，R2和R4阻值变化方向相同，变化的大小均相同。
得出输出为
非线性误差为0.
总结
全桥，灵敏度最高，消除了非线性误差，还具有温度补偿功能。(温度变化四个电阻变化值相同，相对电桥依旧处于平衡)
这篇关于电桥的原理，及非线性误差的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
