4.4 给定的点是否在三角形之内

本文主要是介绍4.4 给定的点是否在三角形之内，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1. 前言

本文的一些图片, 资料 截取自编程之美

2. 问题描述

3. 问题分析

假设给定的三角形为ABC, 给定的点为D, 使用S(ABC) 表示ABC三个点构成的三角形的面积
解法一 : 连接AD, BD, CD, 然后求解S(ABC); S(DBC), S(ADC), S(ABD), 如果S(ABC) == S(DBC) + S(ADC) + S(ABD), 则说明给定的点D是在三角形ABC内部, 否则后者的面积是会大于ABC的面积的

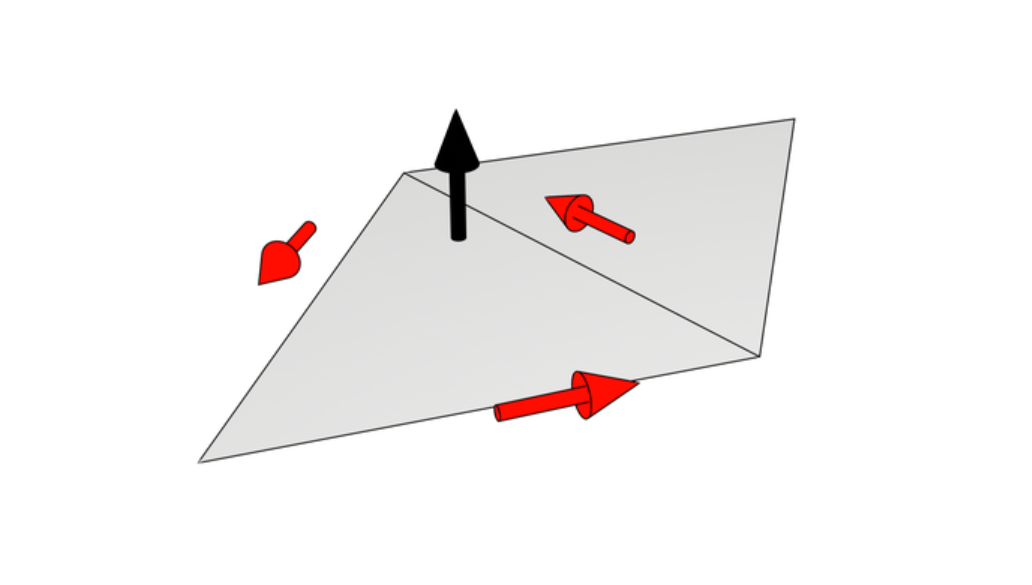
解法二 : 逆时针遍历ABC的三个边, AB, BC, CA, 如果相对于这三个边, D**均**在左边, 则说明D在三角形ABC的内部

可能上面的描述比较抽象, 特别是第二种解法, 下面是一些图解
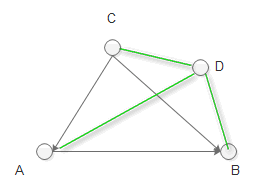
解法一 :
1 D在ABC内部

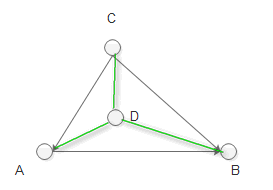
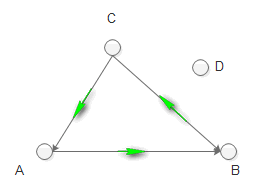
2 D在ABC外部

解法二 :
1 D在ABC内部

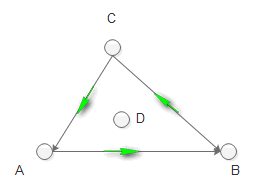
2 D在ABC外部

4. 代码

/*** file name : Test13IsPointInTriangle.java* created at : 9:34:57 AM May 30, 2015* created by 970655147*/package com.hx.test04;public class Test13IsPointInTriangle {// 判断给定的点是否在三角形内部public static void main(String []args) {Point point = new Point(0, 6);Triangle tri = new Triangle(new Point(0, 0), new Point(5, 0), new Point(0, 7) );isPointInTriangle01(point, tri);isPointInTriangle02(point, tri);}// 思路 : 将tri的三个顶点和point连接起来, 然后判断(abd + acd + bcd) 是否大于abc// 如果大于   则说明d在abc之外, 否则说明d在abc之内public static void isPointInTriangle01(Point point, Triangle tri) {double offset = 0.001;Triangle abd = new Triangle(tri.vertex01, tri.vertex02, point);Triangle acd = new Triangle(tri.vertex01, tri.vertex03, point);Triangle bcd = new Triangle(tri.vertex02, tri.vertex03, point);if(abd.getArea() + acd.getArea() + bcd.getArea() > (tri.getArea() + offset) ) {Log.log(false);} else {Log.log(true);}}// 从d开始逆时针旋转   可以发现  点d在边ab, bc, ca的左边   于是便有了下面的方法// 如果点d 在ab, bc, ca的左边   则说明点d存在于该三角形内// 否则  点d在三角形内public static void isPointInTriangle02(Point point, Triangle tri) {if(crossProduct(tri.vertex01, tri.vertex02, point) >= 0.0d && crossProduct(tri.vertex02, tri.vertex03, point) >= 0.0d && crossProduct(tri.vertex03, tri.vertex01, point) >= 0.0d) {Log.log(true);} else {Log.log(false);}}// 表示向量 ab x ad// 如果ab x ad > 0,  则说明d在ab的左边// 如果ab x ad < 0,  则说明d在ab的右边// 如果ab x ad == 0,  则说明d在ab的上private static double crossProduct(Point a, Point b, Point d) {return (b.x - a.x) * (d.y - a.y) - (d.x - a.x) * (b.y - a.y);}// 三角形static class Triangle {// 三个顶点  三个边长Point vertex01, vertex02, vertex03;double edge12, edge23, edge31;// 初始化public Triangle() {}public Triangle(Point vertex01, Point vertex02, Point vertex03) {this.vertex01 = vertex01;this.vertex02 = vertex02;this.vertex03 = vertex03;edge12 = calcEdge(vertex01, vertex02);edge23 = calcEdge(vertex02, vertex03);edge31 = calcEdge(vertex03, vertex01);}// 给定两个顶点  计算他们之间的距离private double calcEdge(Point vertex01, Point vertex02) {return Math.sqrt(Math.pow((vertex01.x - vertex02.x ), 2) + Math.pow((vertex01.y - vertex02.y ), 2) );}// 利用海伦公式求面积public double getArea() {double p = (edge12 + edge23 + edge31) / 2;return Math.sqrt((p - edge12) * (p - edge23) * (p - edge31) * p );}}}

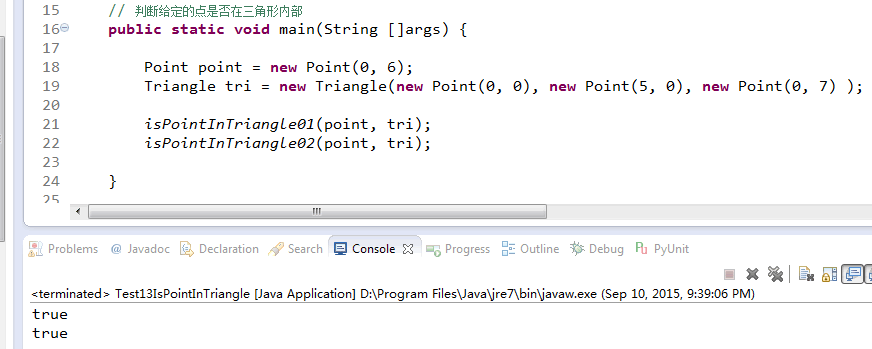
5. 运行结果

6. 总结

这个问题不仅让我了解到了这两种方法, 还有一个收获就是, 了解到了海伦公式, 以及勾股定理的证明

注 : 因为作者的水平有限，必然可能出现一些bug, 所以请大家指出！

这篇关于4.4 给定的点是否在三角形之内的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---