11 是否存在子树 二叉树镜像

本文主要是介绍11 是否存在子树 二叉树镜像，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

前言

本博文部分图片, 思路来自于剑指offer 或者编程珠玑

问题描述

&

思路

对于第一个问题, 判断给定的树[subRoot]是否是给定的树的子树[root]
思路一 : 基于递归, 首先判断给定的两个结点是否为null
     如果两个结点都不为空
        首先判断两个结点的数据是否一致, 如果是 则判断两个子树是否相同, 如果相同 返回true
        否则 递归判断root的左子树中是否存在subRoot匹配的子树, 如果存在 返回true
        否则 递归判断root的右子树中是否存在subRoot匹配的子树, 如果存在 返回true
        如果均没有找到匹配的子树, 返回false
    如果subRoot结点为空 返回true [对于 这两种情况的处理, 只是 我这里是这样处理]
    如果root结点为空 返回false

对于第二个问题, 获取给定树的镜像, 初一看是否是感觉挺神奇的, 书中给出了思路一, 思路二 是使用一个容器来维护需要交换的结点, 进行交换

思路一 : 首先将给定的结点左右子树互换, 然后递归处理左右子树

思路二 : 利用一个容器来维护需要交换的结点, 然后获取容器中的对象, 进行结点的交换

参考代码

/*** file name : Test04isSubTreeExists.java* created at : 8:51:10 PM Jun 6, 2015* created by 970655147*/package com.hx.test05;public class Test04isSubTreeExists {// 1. 判断一棵树中是否含有[存在] 另一颗数的结构// 2. 获取一棵树的镜像public static void main(String []args) {String data = "58 34 12 # # 42 # # 78 68 69 # # # 99 # #";BinTree tree = BinTree.createABinTree(data);String subData = "34 11 # # 42 # #";
//      String subData = "78 68 # # 99 # # #";BinTree subTree = BinTree.createABinTree(subData);boolean isSubTreeExist = isSubTreeExists(tree.root(), subTree.root() );Log.log(isSubTreeExist);getMirrorOfTree(tree.root() );
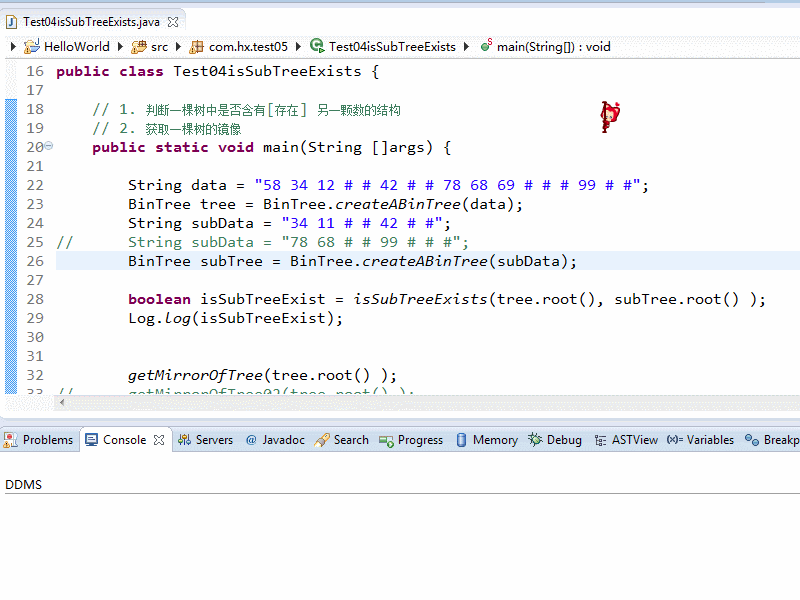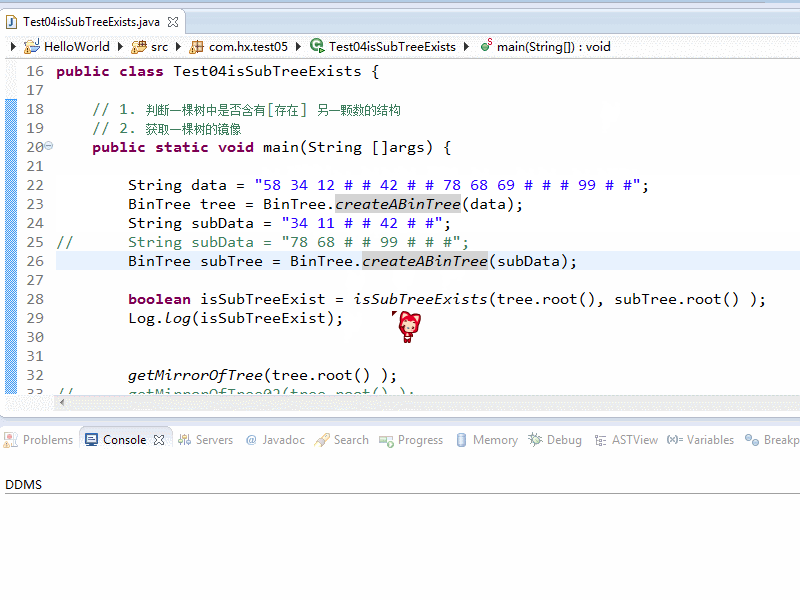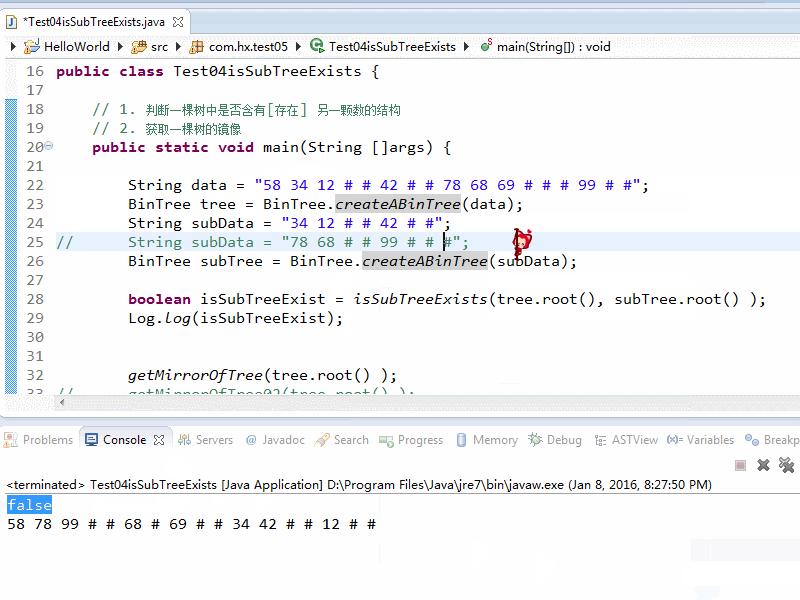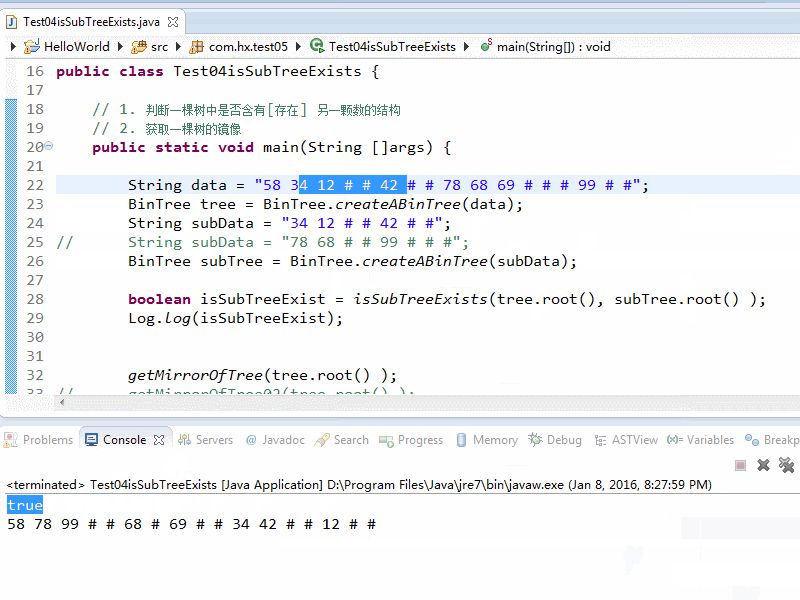
//      getMirrorOfTree02(tree.root() );Log.log(tree);}// 判断node所在的树  是否存在和subRoot结构一样的子树// 思路 : 如果node节点和subRoot节点都不为空  则比较两个结点的数据, 如果两个结点的数据相同   则判断node中是否存在和subRoot结构一致的子树// 否则  如果node的左子树不为null   递归比较左子树// 否则  如果node的右子树不为null   递归比较右子树// 如果以上三种情况[node结点和subRoot结点数据相同, 递归的左子树, 右子树]任意   一个存在相同的结构, 返回true// 否则如果  subRoot结点为null 返回true// 否则如果  node结点为null    返回false// 不可能到达这里// 否则如果  node结点和subRoot结点均为null  返回truepublic static boolean isSubTreeExists(Node node, Node subRoot) {if(!BinTree.isNodeNull(node) && !BinTree.isNodeNull(subRoot)) {boolean isSubTreeExist = false;if(subRoot.getData().equals(node.getData()) ) {isSubTreeExist = isSubTree(node, subRoot);if(isSubTreeExist) {return true;}} if(!BinTree.isNodeNull(node.getLeft()) ) {isSubTreeExist = isSubTreeExists(node.getLeft(), subRoot );if(isSubTreeExist) {return true;}}if(!BinTree.isNodeNull(node.getRight()) ) {isSubTreeExist = isSubTreeExists(node.getRight(), subRoot );    }return isSubTreeExist;} else if(BinTree.isNodeNull(subRoot)) {return true;} else if(BinTree.isNodeNull(node)) {return false;// can't get there...}else {return true;}}// 获取node结点为根节点的树的镜像   递归实现public static void getMirrorOfTree(Node node) {Node tmp = node.getRight();node.setRight(node.getLeft() );node.setLeft(tmp );if(!BinTree.isNodeNull(node.getLeft()) ) {getMirrorOfTree(node.getLeft() );}if(!BinTree.isNodeNull(node.getRight()) ) {getMirrorOfTree(node.getRight() );}}// 获取node结点为根节点的树的镜像   仿递归实现public static void getMirrorOfTree02(Node node) {Deque<Node> nodes = new LinkedList<Node>();nodes.push(node);while(nodes.size() > 0) {Node top = nodes.pop();Node tmp = top.getRight();top.setRight(top.getLeft() );top.setLeft(tmp );if(!BinTree.isNodeNull(top.getLeft()) ) {nodes.push(top.getLeft() );}if(!BinTree.isNodeNull(top.getRight()) ) {nodes.push(top.getRight() );}}}// 判断node结点是否和subRoot结点结构一致[subRoot结点是node结点所在的树的子集]// 先判断左子树  如果左子树不相同  直接返回false[视为node中不可能存在subRoot的结构 // 在判断右子树  如果左右子树  均相同   则视为存在subRoot的结构   返回trueprivate static boolean isSubTree(Node node, Node subRoot) {boolean isLeftEqual = false, isRightEqual = false;if(!BinTree.isNodeNull(node.getLeft())  && !BinTree.isNodeNull(subRoot.getLeft())  ) {isLeftEqual = node.getLeft().getData().equals(subRoot.getLeft().getData() ) ;if(isLeftEqual) {isLeftEqual = isSubTree(node.getLeft(), subRoot.getLeft() );}} else if(BinTree.isNodeNull(subRoot.getLeft()) ) {isLeftEqual = true;} else if(BinTree.isNodeNull(node.getLeft()) ) {isLeftEqual = false;}if(!isLeftEqual) {return false;}if(!BinTree.isNodeNull(node.getRight()) && !BinTree.isNodeNull(subRoot.getRight())  ) {isRightEqual = node.getRight().getData().equals(subRoot.getRight().getData() );if(isRightEqual) {isRightEqual = isSubTree(node.getRight(), subRoot.getRight() );}} else if(BinTree.isNodeNull(subRoot.getRight()) ) {isRightEqual = true;} else if(BinTree.isNodeNull(node.getRight()) ) {isRightEqual = false;}return (isLeftEqual && isRightEqual);}}

效果截图

总结

关于树的算法, 很多东西都涉及到了递归

注 : 因为作者的水平有限，必然可能出现一些bug, 所以请大家指出！

这篇关于11 是否存在子树 二叉树镜像的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---