本文主要是介绍【链表】Leetcode 82. 删除排序链表中的重复元素 II【中等】,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
删除排序链表中的重复元素 II
- 给定一个已排序的链表的头 head , 删除原始链表中所有重复数字的节点,只留下不同的数字 。返回 已排序的链表 。
示例 1:
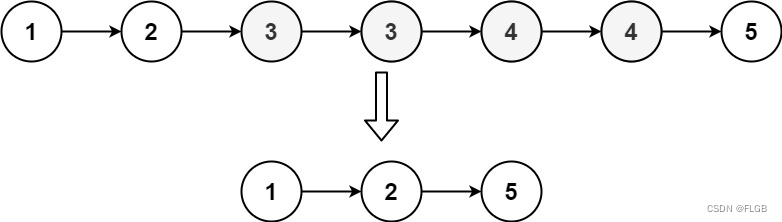
输入:head = [1,2,3,3,4,4,5]
输出:[1,2,5]
解题思路
由于链表是已排序的,所以重复的节点会相邻出现。可以使用双指针法来解决这个问题,一个指针用于遍历链表,另一个指针用于跟踪上一个未重复的节点。
- 遍历链表:使用两个指针pre和current。pre用于指向上一个未重复的节点,current用于遍历链表。
- 删除重复节点:如果current和current.next的值相等,则继续向前遍历直到遇到不同的值为止。将pre.next指向当前遇到的第一个不同值节点。
- 移动指针:如果current和current.next的值不同,pre移动到current位置,current继续向前遍历。
- 返回结果:返回哨兵节点的下一个节点。
Java实现
public class DeleteDuplicates {public static class ListNode {int val;ListNode next;ListNode(int x) { val = x; }}public ListNode deleteDuplicates(ListNode head) {// 创建哨兵节点ListNode dummy = new ListNode(0);dummy.next = head;ListNode pre = dummy;ListNode current = head;while (current != null) {// 跳过当前节点后面所有的重复节点while (current.next != null && current.val == current.next.val) {current = current.next;}// 如果pre的下一个节点是current,说明当前节点没有重复if (pre.next == current) {pre = pre.next;} else {// 如果pre的下一个节点不是current,说明有重复节点,跳过所有重复节点pre.next = current.next;}current = current.next;}return dummy.next;}public static void main(String[] args) {DeleteDuplicates deleteDuplicates = new DeleteDuplicates();// 创建示例链表 1->2->3->3->4->4->5ListNode head = new ListNode(1);head.next = new ListNode(2);head.next.next = new ListNode(3);head.next.next.next = new ListNode(3);head.next.next.next.next = new ListNode(4);head.next.next.next.next.next = new ListNode(4);head.next.next.next.next.next.next = new ListNode(5);// 删除重复节点ListNode newHead = deleteDuplicates.deleteDuplicates(head);printList(newHead); // 输出: 1->2->5}// 辅助方法:打印链表public static void printList(ListNode head) {ListNode current = head;while (current != null) {System.out.print(current.val);if (current.next != null) {System.out.print("->");}current = current.next;}System.out.println();}
}
时间空间复杂度
- 时间复杂度:O(n),其中 n 是链表的节点数。需遍历链表一次。
- 空间复杂度:O(1),只使用了几个额外的指针。
这篇关于【链表】Leetcode 82. 删除排序链表中的重复元素 II【中等】的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





