Oracle实践｜内置函数之数学型函数

本文主要是介绍Oracle实践｜内置函数之数学型函数，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

📫 作者简介：「六月暴雪飞梨花」，专注于研究Java，就职于科技型公司后端工程师
🏆 近期荣誉：华为云云享专家、阿里云专家博主、腾讯云优秀创作者、ACDU成员
🔥 三连支持：欢迎 ❤️关注、👍点赞、👉收藏三连，支持一下博主~

序言

背景说明

Oracle 数据库提供了丰富的内置函数，涵盖数值处理、字符串操作、日期和时间处理、逻辑判断、集合处理、数据分析、数据类型转换等多个方面。下面就随着我一起来学习下这个内置函数吧，有解释不到之处，还望批评指正。
Oracle 数据库提供了一系列数学类型的函数，主要有数值处理部分和数学符号判断函数，用于数学方面的数值计算和简单的数值转换。

示例环境

本篇示例是基于Oracle DB 19c EE （19.17.0.0.0）版本操作，所操作的环境依旧是oracle提供的在线测试环境。如果有不同之处，请指出。

1 数学数值处理

在非统计计算、金融相关行业，这些内置函数使用频率较少，只需要了解即可，不做强制掌握。

绝对值–ABS

【定义】

ABS(number)：返回数字的绝对值（任何数的绝对值都是非负数）。

【示例】
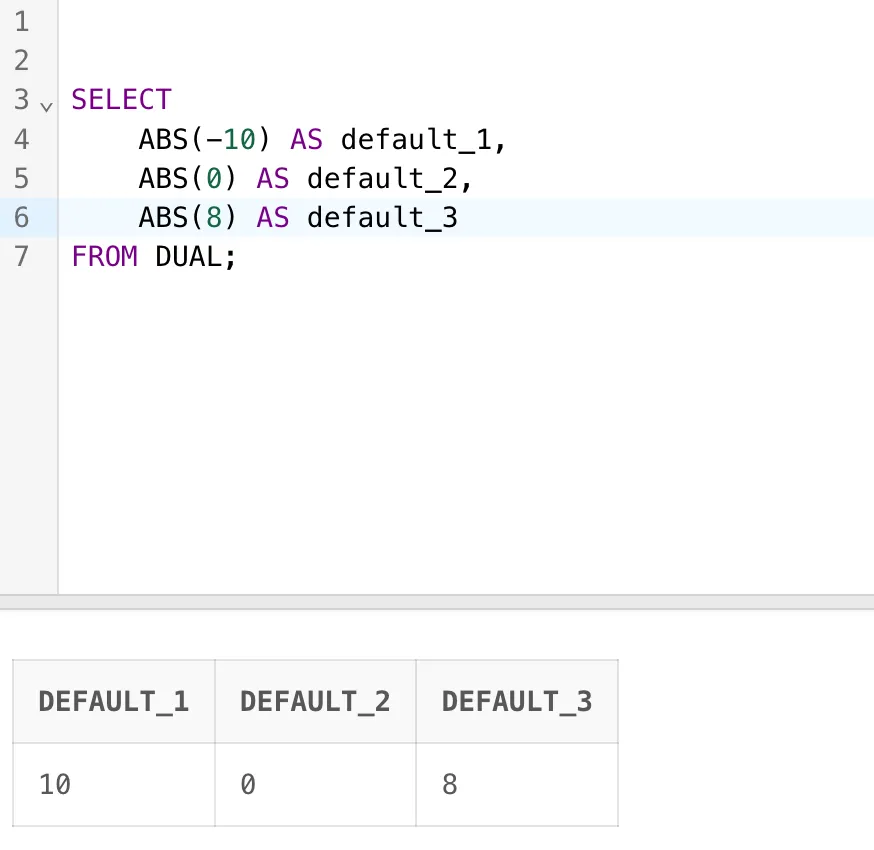
分别获取 -10 的绝对值，0 的绝对值，8 的绝对值，

SELECT ABS(-10) AS default_1,ABS(0) AS default_2,ABS(8) AS default_3
FROM DUAL;

取余–MOD

【定义】

MOD(n1, n2)：返回n1除以n2的余数。

【示例】
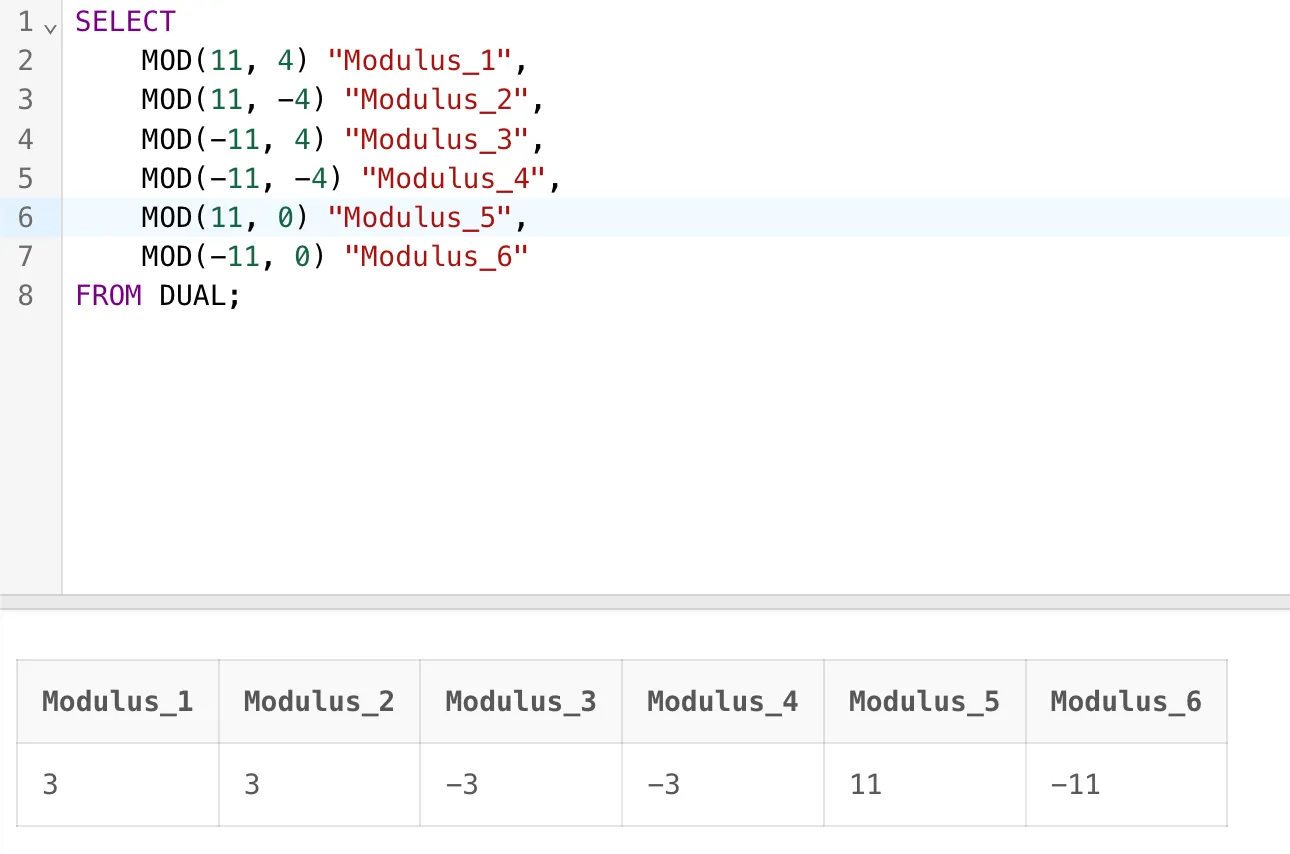
如果n2为0，则返回n1，例如示例中的Modulus_5、Modulus_6此函数同我们数学上的取模还有些不一样。
如果n2不为0，返回值为数学中的取模后的数值，状态为n1的状态（当n1为正数时返回正数状态，当n1为负数状态时，返回值为负数状态）。

SELECT MOD(11, 4) "Modulus_1",MOD(11, -4) "Modulus_2",MOD(-11, 4) "Modulus_3",MOD(-11, -4) "Modulus_4",MOD(11, 0) "Modulus_5",MOD(-11, 0) "Modulus_6"
FROM DUAL;

注意⚠️：代码部分参考官方的数据值。此时有可能有疑问，如果 0 对 0 取模会发生什么呢？其实，对照上述的定义，思考下答案就不言而喻了。

数值截取–TRUNC

下面这几个函数比较常用，尤其是在金融计算方面。
【定义】

TRUNC(number[, decimal_places])：截去数字的小数部分，可选地保留指定小数位数。

注意⚠️：这个函数还有一个日期类型的参数，请参考上一篇「日期与时间的函数」。

【示例】
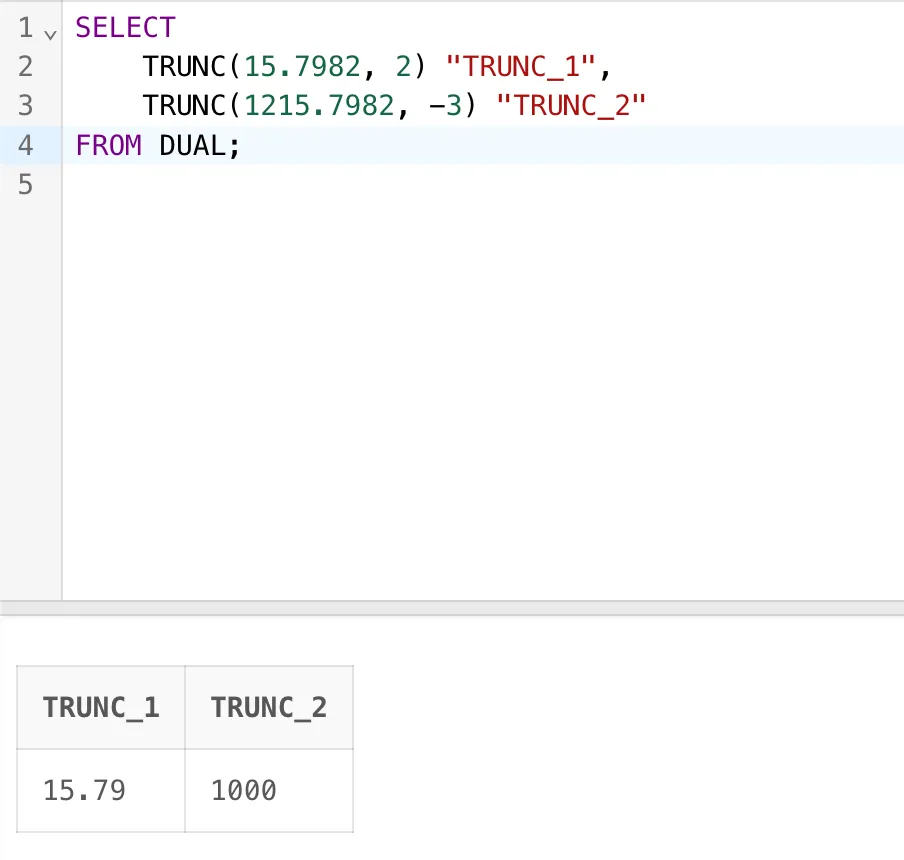
当给定一个数值后，如果 decimal_places 为正整数，那么就是保留小数的位数，例如15.7982, 其中decimal_places = 2，那么就是执行完后的结果为15.79。
当给定一个数值后，如果 decimal_places 为负整数，那么就是去掉小数部分后，从蒸熟部分开始从右向左置为几位0（截取不足部分补充 0 ），例如 1215.7982 ，其中decimal_places = -3，那么就是执行完后的结果为1000。

SELECT TRUNC(15.7982, 2) "TRUNC_1",TRUNC(1215.7982, -3) "TRUNC_2" 
FROM DUAL;

随机数–ROUND

【定义】

ROUND(number[, decimal_places])：四舍五入数字到指定小数位数。这个函数已经使用的比较频繁了，这里不在赘述，有点类似上面的函数，其实了解参数的含义，那么就是实践了。

向上/下取整–CEIL/FLOOR

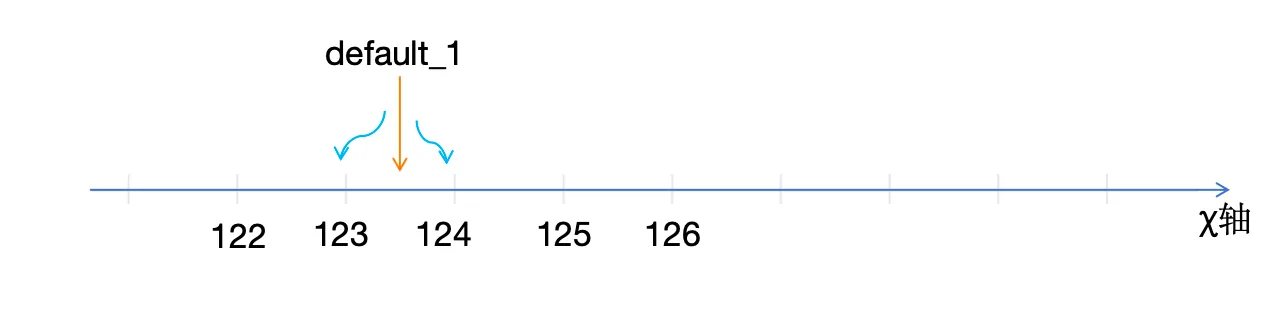
这个函数的用途是不是很熟悉，以前在饭馆（作者老家都是饭馆，饭店，一般不会写餐馆）吃饭结账时，我们的账单是一个很好的例子，例如结帐时123.5元，那么一般会收取123元。
【定义】

CEIL(number)：返回大于或等于number的最小整数（向上取整），例如CEIL(123.45) = 124。

FLOOR(number)：返回小于或等于给number最大整数（向下取整），例如FLOOR(123.45) = 123。

【示例】

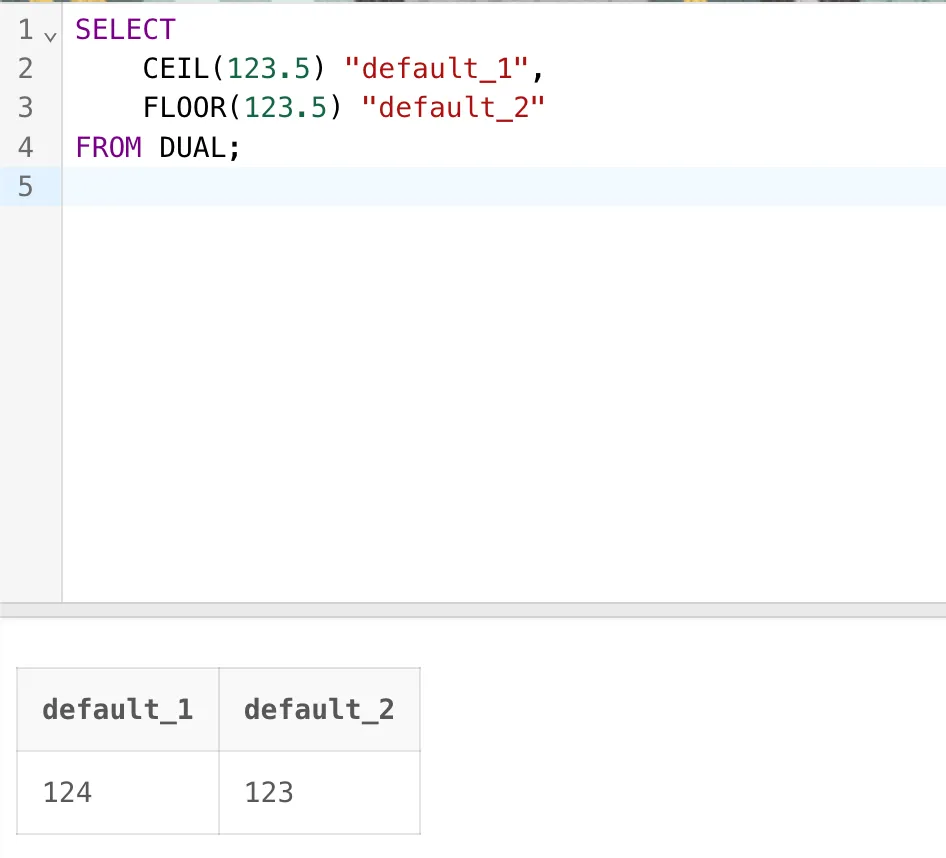
SELECT CEIL(123.5) "default_1",FLOOR(123.5) "default_2" 
FROM DUAL;

数学运算

不常用的一些函数，一般的科学类的使用的频率比较高。
【定义】

POWER(base, exponent)：返回base的exponent次幂，例如2的3次幂方等于8，在数学上公式为 2^3 = 8。

SQRT(number)：返回number的平方根，例如4的平方根为2，在数学上公式表示为 √4 = 2。

LN(number), LOG(number[, base])：自然对数和基于特定基数的对数（不常用的就不写了，可以参考下官方指导文档）。

2 数学符号判断

【定义】
SIGN(number)：返回数字的符号，常用的就是判断一个数字的状态（1代表正数，0代表零，-1代表负数）。
【示例】

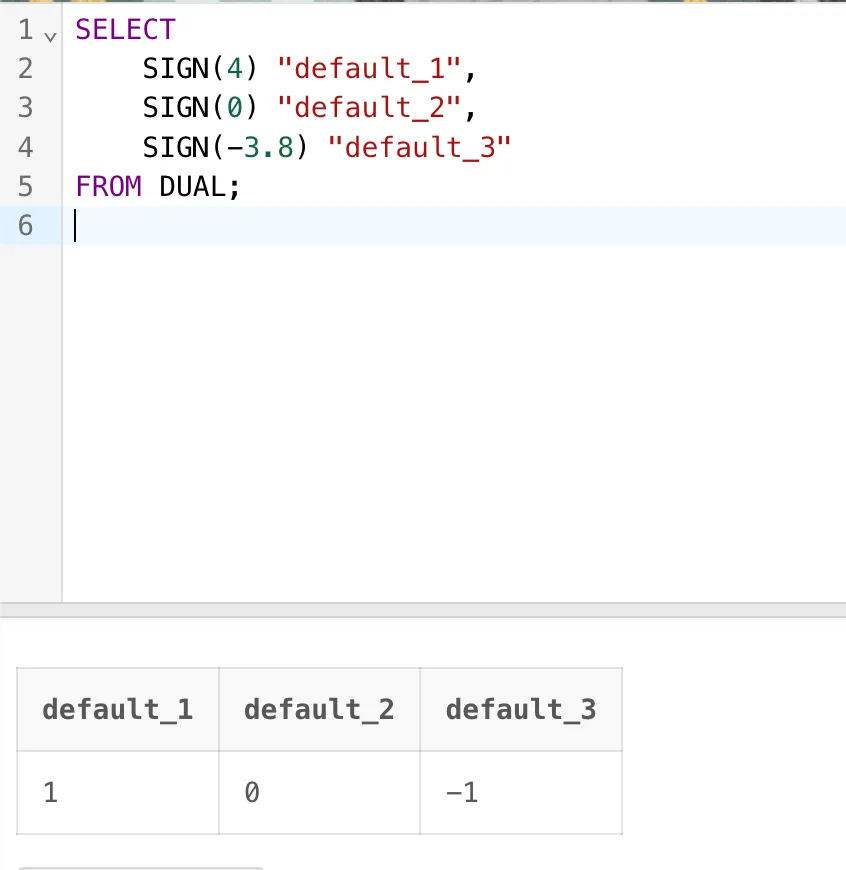
SELECT SIGN(4) "default_1",SIGN(0) "default_2", SIGN(-3.8) "default_3" 
FROM DUAL;

总结

在数学函数或者统计函数上，常用的一半都是在SELECT中做计算或数值转换，不过我们一般在使用子句中使用转换参数值再来使用列查询去做匹配，这样子做的好处是会走索引，如果使用在SELECT上，会隐式转换为临时字段，此时会增加查询时间，消耗性能。

---

欢迎关注博主 「六月暴雪飞梨花」 或加入【六月暴雪飞梨花社区】一起学习和分享Linux、C、C++、Python、Matlab，机器人运动控制、多机器人协作，智能优化算法，滤波估计、多传感器信息融合，机器学习，人工智能等相关领域的知识和技术。

这篇关于Oracle实践｜内置函数之数学型函数的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---