2022年CSP-J入门级第一轮初赛真题

本文主要是介绍2022年CSP-J入门级第一轮初赛真题，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

一、单项选择题（共15题，每题2分，共计30分；每题有且仅有一个正确选项）

第 1 题 在内存储器中每个存储单元都被赋予一个唯一的序号，称为（）。

• A. 地址
• B. 序号
• C. 下标
• D. 编号

第 2 题 编译器的主要功能是（ ）。

• A. 将源程序翻译成机器指令代码
• B. 将源程序重新组合
• C. 将低级语言翻译成高级语言
• D. 将一种高级语言翻译成另一种高级语言

第 3 题 设 x=true,y=true,z=false，以下逻辑运算表达式值为真的是（ ）。

• A. (y∨z)∧x∧z
• B. x∧(z∨y) ∧z
• C. (x∧y) ∧z
• D. (x∧y)∨(z∨x)

第 4 题 现有一张分辨率为 2048×1024 像素的 32 位真彩色图像。请问要存储这张图像，需要多大的存储空间？（ ）。

• A. 16MB
• B. 4MB
• C. 8MB
• D. 2MB

第 5 题 冒泡排序算法的伪代码如下：
输入：数组L, n ≥ k。输出：按非递减顺序排序的 L。

输入：数组L, n ≥ k。输出：按非递减顺序排序的 L。
算法 BubbleSort：
1. FLAG ← n //标记被交换的最后元素位置
2. while FLAG > 1 do
3.     k ← FLAG -1
4.     FLAG ← 1
5.     for j=1 to k do
6.         if L(j) > L(j+1) then do
7.              L(j)  ↔ L(j+1)
8.              FLAG ← j

对 n 个数用以上冒泡排序算法进行排序，最少需要比较多少次?（ ）。

• A. (2^n)
• B. (n−2)
• C. (n−1)
• D. n

第 6 题 设 (A) 是 (n) 个实数的数组，考虑下面的递归算法：

XYZ (A[1..n])  
1.  if n=1 then return A[1]  
2.  else temp ← XYZ (A[1..n-1])  
3.  if temp < A[n]  
4.  then return temp  
5.  else return A[n]  

请问算法 XYZ 的输出是什么？（）。

• A. A 数组的平均
• B. A 数组的最小值
• C. A 数组的中值
• D. A 数组的最大值

第 7 题 链表不具有的特点是（）。

• A. 可随机访问任一元素
• B. 不必事先估计存储空间
• C. 插入删除不需要移动元素
• D. 所需空间与线性表长度成正比

第 8 题 有 10 个顶点的无向图至少应该有（ ）条边才能确保是一个连通图。

• A. 9
• B. 10
• C. 11
• D. 12

第 9 题 二进制数 1011 转换成十进制数是（ ）。

• A. 11
• B. 10
• C. 13
• D. 12

第 10 题 5 个小朋友并排站成一列，其中有两个小朋友是双胞胎，如果要求这两个双胞胎必须相邻，则有（ ）种不同排列方法?

• A. 48
• B. 36
• C. 24
• D. 72

第 11 题 下图中所使用的数据结构是（ )。

• A. 栈
• B. 队列
• C. 二叉树
• D. 哈希表

第 12 题 独根树的高度为 1。具有 61 个结点的完全二叉树的高度为（ ）。

• A. 7
• B. 8
• C. 5
• D. 6

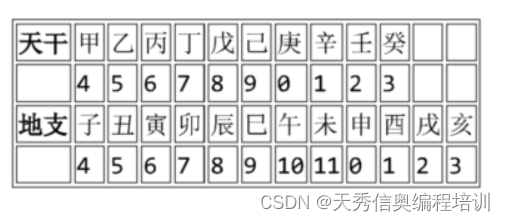
第 13 题 干支纪年法是中国传统的纪年方法，由 10 个天干和 12 个地支组合成 60 个天干地支。由公历年份可以根据以下公式和表格换算出对应的天干地支。

• 天干 =（公历年份）除以 10所得余数
• 地支 =（公历年份）除以 12 所得余数
  
  例如，今年是 2020 年，2020 除以 10 余数为 0，查表为"庚”；2020 除以 12，余数为 4，查表为“子” 所以今年是庚子年。
  请问 1949 年的天干地支是（ ）
• A. 己酉
• B. 己亥
• C. 己丑
• D. 己卯

第 14 题 10 个三好学生名额分配到 7 个班级，每个班级至少有一个名额，一共有（ ）种不同的分配方案。

• A. 84
• B. 72
• C. 56
• D. 504

第 15 题 有五副不同颜色的手套（共 10 只手套，每副手套左右手各 1 只），一次性从中取 6 只手套，请问恰好能配成两副手套的不同取法有（ ）种。

• A. 120
• B. 180
• C. 150
• D. 30

二、阅读程序

（程序输入不超过数组或字符串定义的范围；判断题正确填 √，错误填 ×。除特殊说明外，判断题 1.5 分，选择题 3 分，共计 40 分）

1

#include <cstdlib>
#include <iostream>
using namespace std;char encoder[26] = {'C','S','P',0};
char decoder[26];string st;int main()  {int k = 0;for (int i = 0; i < 26; ++i)if (encoder[i] != 0) ++k;for (char x ='A'; x <= 'Z'; ++x) {bool flag = true;for (int i = 0; i < 26; ++i)if (encoder[i] ==x) {flag = false;break;}if (flag) {encoder[k]= x;++k;}}for (int i = 0; i < 26; ++i)decoder[encoder[i]- 'A'] = i + 'A';cin >> st;for (int i = 0; i < st.length( ); ++i)st[i] = decoder[st[i] -'A'];cout << st;return 0;
}

判断题

1.输入的字符串应当只由大写字母组成，否则在访问数组时可能越界。（ ）

2.若输入的字符串不是空串，则输入的字符串与输出的字符串一定不一样。（）

3.将第 12 行的 i < 26 改为 i < 16，程序运行结果不会改变。（ ）

4.将第 26 行的 i < 26 改为 i < 16，程序运行结果不会改变。（ ）

单选题

5） 若输出的字符串为 ABCABCABCA，则下列说法正确的是（ ）。

• A. 输入的字符串中既有 S 又有 P
• B. 输入的字符串中既有 S 又有 B
• C. 输入的字符串中既有 A 又有 P
• D. 输入的字符串中既有 A 又有 B

6）若输出的字符串为 CSPCSPCSPCSP，则下列说法正确的是（ ）。

• A. 输入的字符串中既有 P 又有 K
• B. 输入的字符串中既有 J 又有 R
• C. 输入的字符串中既有 J 又有 K
• D. 输入的字符串中既有 P 又有 R

了解了，下面是根据您的要求使用“>”符号进行格式化的输出示例：

2

#include <iostream>
using namespace std;long long n, ans;
int k, len;
long long d[1000000];int main() {cin >> n >> k;d[0] = 0;len = 1;ans = 0;for (long long i = 0; i < n; ++i) {++d[0];for (int j = 0; j + 1 < len; ++j) {if (d[j] == k) {d[j] = 0;d[j + 1] += 1;++ans;}}if (d[len - 1] == k) {d[len - 1] = 0;d[len] = 1;++len;++ans;}}cout << ans << endl;return 0;
}

假设输入的 ( n ) 是不超过 ( 2^(62) ) 的正整数，( k ) 都是不超过 10000 的正整数，完成下面的判断题和单选题：

判断题

第 1 题 若 ( k=1 )，则输出 ( ans ) 时，( len=n )。（ ）

第 2 题 若 ( k>1 )，则输出 ( ans ) 时，( len ) 一定小于 ( n )。（ ）

第 3 题 若 ( k>1 )，则输出 ( ans ) 时，( len ) 一定大于 ( n )。（ ）

单选题

第 4 题 若输入的 ( n ) 等于 10^(15)，输入的 ( k ) 为 1，则输出等于（ ）。

第 5 题 若输入的 ( n ) 等于 205,891,132,094,649（即 30），输入的 ( k ) 为 33，则输出等于（ ）。

第 6 题 若输入的 ( n ) 等于 100,010,002,000,090，输入的 ( k ) 为 10，则输出等于（ ）。

• A. 11,112,222,444,543
• B. 11,122,222,444,453
• C. 11,122,222,444,543
• D. 11,112,222,444,453

3

#include <algorithm>
#include <iostream>
using namespace std;                     int n;                                   
int d[50][2];                            
int ans;                                 void dfs(int n, int sum) {               if (n == 1) {                            ans = max(sum, ans);           return;                                   }                                        for (int i = 1; i < n; ++i) {            int a = d[i - 1][0], b = d[i - 1][1];  int x = d[i][0], y = d[i][1];            d[i - 1][0] = a + x;                     d[i - 1][1] = b + y;                     for (int j = i; j < n - 1; ++j)            d[j][0] = d[j + 1][0], d[j][1] = d[j + 1][1];int s = a + x + abs(b - y);              dfs(n - 1, sum + s);                    for (int j = n - 1; j > i; --j)          d[j][0] = d[j - 1][0], d[j][1] = d[j - 1][1];d[i - 1][0] = a, d[i - 1][1] = b;        d[i][0] = x, d[i][1] = y;                }                                        
}                                        int main() {                             cin >> n;                                for (int i = 0; i < n; ++i)              cin >> d[i][0];for (int i = 0; i < n; ++i)cin >> d[i][1];ans = 0;dfs(n, 0);cout << ans << endl;return 0;
}

假设输入的 n 是不超过 50 的正整数，( d[i][0] )、( d[i][1] ) 都是不超过 10000 的正整数，完成下面的判断题和单选题：

判断题

第 1 题 若输入n 为 0，此程序可能会死循环或发生运行错误。（ ）

第 2 题 若输入 ( n ) 为 20，接下来的输入全为 0，则输出为 0。（ ）

第 3 题 输出的数一定不小于输入的 ( d[i][0] ) 和 ( d[i][1] ) 的任意一个。（ ）

单选题

第 4 题 若输入的 ( n ) 为 20，接下来的输入是 20 个 9 和 20 个 0，则输出为（ ）。

• A. 1890
• B. 1881
• C. 1908
• D. 1917

第 5 题 若输入的 ( n ) 为 30，接下来的输入是 30 个 0 和 30 个 5，则输出为（ ）。

• A. 2000
• B. 2010
• C. 2030
• D. 2020

第 6 题 （4 分）若输入的 ( n ) 为 15，接下来的输入是 15 到 1，以及 15 到 1，则输出为（ ）。

• A. 2440
• B. 2220
• C. 2240
• D. 2420

三、完善程序（单选题，每小题3分，共计30分）

1.

（质因数分解）给出正整数 ( n )，请输出将 ( n ) 质因数分解的结果，结果从小到大输出。

例如：输入 ( n = 120 )，程序应该输出 2 2 2 3 5，表示： ( 120 = 2 * 2 * 2 * 3 * 5 )。输入保证 ( 2 ≤ n ≤ 10^9 )。

提示：先从小到大枚举变量 ( i )，然后用 ( i ) 不停试除 ( n ) 来寻找所有的质因子。

试补全程序。

#include <cstdio>
using namespace std;
int n, i;int main() {scanf("%d", &n);for(i = ①; ② <= n; i++){③{printf("%d ", i);n = n / i;}}if(④)printf("%d ", ⑤);return 0;
}

选择题

第 1 题 ①处应填（ ）

• A. 1
• B. n-1
• C. 2
• D. 0

第 2 题 ②处应填（ ）

• A. n/i
• B. n/(i*i)
• C. i*i
• D. iii

第 3 题 ③处应填（ ）

• A. if(n%i==0)
• B. if(i*i<=n)
• C. while(n%i==0)
• D. while(i*i<=n)

第 4 题 ④处应填（ ）

• A. n>1
• B. n<=1
• C. i<n/i
• D. i+i<=n

第 5 题 ⑤处应填（ ）

• A. 2
• B. n/i
• C. n
• D. i

2

（最小区间覆盖）给出n个区间，第 i 个区间的左右端点是 ([a_i, b_i])。现在要在这些区间中选出若干个，使得区间 ([0, m]) 被所选区间的并覆盖（即每一个 (0 ≤ i ≤ m) 都在某个所选的区间中）。保证答案存在，求所选区间个数的最小值。

输入第一行包含两个整数 ( n ) 和 ( m ) （(1 ≤ n ≤ 5000), (1 ≤ m ≤ 10^9)）

接下来 ( n ) 行，每行两个整数 ( a_i, b_i ) (0 ≤ a_i, b_i ≤ m)。

提示：使用贪心法解决这个问题。先用 (O(n^2)) 的时间复杂度排序，然后贪心选择这些区间。

试补全程序。

#include <iostream>using namespace std;const int MAXN = 5000;
int n, m;
struct segment { int a, b; } A[MAXN];void sort() // 排序
{for (int i = 0; i < n; i++)for (int j = 1; j < n; j++)if (①){segment t = A[j];②}
}int main()
{cin >> n >> m;for (int i = 0; i < n; i++)cin >> A[i].a >> A[i].b;sort();int p = 1;for (int i = 1; i < n; i++)if (③)A[p++] = A[i];n = p;int ans =0, r = 0;int q = 0;while (r < m){while (④)q++;⑤;ans++;}cout << ans << endl;return 0;
}

选择题

第 1 题 ①处应填（ ）

• A. A[j].b > A[j-1].b
• B. A[j].a < A[j-1].a
• C. A[j].a > A[j-1].a
• D. A[j].b < A[j-1].b

第 2 题 ②处应填（ ）

• A. A[j+1] = A[j]; A[j] = t;
• B. A[j-1] = A[j]; A[j] = t;
• C. A[j] = A[j+1]; A[j+1] = t;
• D. A[j] = A[j-1]; A[j-1] = t;

第 3 题 ③处应填（ ）

• A. A[i].b > A[p-1].b
• B. A[i].b < A[i-1].b
• C. A[i].b > A[i-1].b
• D. A[i].b < A[p-1].b

第 4 题 ④处应填（ ）

• A. q+1 < n && A[q+1].a <= r
• B. q+1 < n && A[q+1].b <= r
• C. q < n && A[q].a <= r
• D. q < n && A[q].b <= r

第 5 题 ⑤处应填（ ）

• A. r = max(r, A[q+1].b)
• B. r = max(r, A[q].b)
• C. r = max(r, A[q+1].a)
• D. q++

这篇关于2022年CSP-J入门级第一轮初赛真题的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---