457专题
【优化算法】蜉蝣优化算法(MA)【含Matlab源码 457期】
⛄一、获取代码方式 获取代码方式1: 完整代码已上传我的资源:【优化算法】蜉蝣优化算法(MA)【含Matlab源码 457期】 点击上面蓝色字体,直接付费下载,即可。 获取代码方式2: 付费专栏Matlab优化求解(初级版) 备注: 点击上面蓝色字体付费专栏Matlab优化求解(初级版),扫描上面二维码,付费29.9元订阅海神之光博客付费专栏Matlab优化求解(初级版),凭支付凭证,私信博
《457数据结构》大纲---不知道是不是真的,也不知道是那一年的
《457数据结构》 一、适用于报考的专业 二、题目类型:简答题、选择题 、算法设计题 三、参考教材:《数据结构(C语言版)》 编者:严蔚敏 清华大学出版社 四、基本内容: 1.数据结构的基本概念、算法的时间复杂度和空间复杂度的定义和表示方法。 2.线性表、栈、队列的逻辑结构、存储结构及其相关算法。
Marketing Plan Pro 出现Runtime Error '457'
保存和下载了一些Example plan之后, 俺的Windows XP home又出现了 每次打开marketing Plan Pro都 运行时间错误 '457' 发现需要删掉一个注册表键值或文件夹或键名来解决这个问题. Windows Registry Editor Version 5.00 [-HKEY_CURRENT_USER/Software/Palo A
leetcode:457. 环形数组是否存在循环
环形数组是否存在循环 存在一个不含 0 的 环形 数组 nums ,每个 nums[i] 都表示位于下标 i 的角色应该向前或向后移动的下标个数: 如果 nums[i] 是正数,向前(下标递增方向)移动 |nums[i]| 步 如果 nums[i] 是负数,向后(下标递减方向)移动 |nums[i]| 步 因为数组是 环形 的,所以可以假设从最后一个元素向前移动一步会到达第一个元素,而第一个元素
leetcode:457. 环形数组是否存在循环
环形数组是否存在循环 存在一个不含 0 的 环形 数组 nums ,每个 nums[i] 都表示位于下标 i 的角色应该向前或向后移动的下标个数: 如果 nums[i] 是正数,向前(下标递增方向)移动 |nums[i]| 步 如果 nums[i] 是负数,向后(下标递减方向)移动 |nums[i]| 步 因为数组是 环形 的,所以可以假设从最后一个元素向前移动一步会到达第一个元素,而第一个元素
Python周刊457期
Python周刊 欢迎阅读《 Python周刊》第457期。 写在前面:翻译不易,欢迎阅读;水平有限,万望海涵。部分链接可能需要特殊的上网方式(😓)。欢迎关注微信公众号“Python小灶,和我一起每天学习Python新知识” 文章、教程和讲座 如何使用吉他编码 学习如何使用吉他而不是键盘进行编程。使用一些自定义的Python代码和其他一些插件,该指导者创建了一些将原始吉他信号转换为按键的
OCP-1Z0-053-V12.02-457题
457.If two windows overlap, which window attribute will determine whether one should be chosen over the other? A. WINDOW_PRIORITY B. PRIORITY C. PRIORITY_LEVEL D. WINDOW_PRIORITY_LEVEL E. OVERLAP
Codeforces Round #457 (Div. 2) B. Jamie and Binary Sequence(二进制,思路,贪心)
描述 Jamie is preparing a Codeforces round. He has got an idea for a problem, but does not know how to solve it. Help him write a solution to the following problem: Find k integers such that the sum
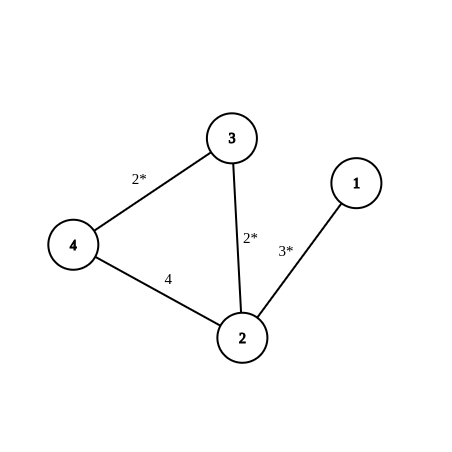
Codeforces Round #457 (Div. 2) C. Jamie and Interesting Graph(构造)
描述 Jamie has recently found undirected weighted graphs with the following properties very interesting: The graph is connected and contains exactly n vertices and m edges. All edge weights are inte