1749专题
SWUN OJ 1749(DP + 线段树)
SWUN 1749 题目链接 思路:lis一样的状态转移方程,不过要利用线段树去维护,每次更新到i,相应的维护i - d之后的区间的最大值,不断转移即可 代码: #include <cstdio>#include <cstring>#include <algorithm>using namespace std;#define lson(x) ((x<<1)+1)#de
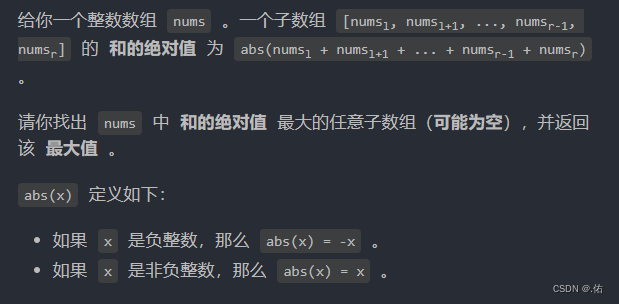
leetcode 1749.任意子数组和的绝对值的最大值
思路:dp 说到绝对值,大家肯定不陌生,但是用在dp上就会使问题变得稍微复杂一些了。 我们在最大子数组和的那道题中知道,在状态转移的时候,我们会舍弃掉为负数的连续部分,重新构建连续的子串。但是,这里不一样,我们并不能轻易舍弃负数的部分,负数也可能让这个子数组和的绝对值变成最大的,例如0,-1000,1,2这个序列就很典型,我们如果按照上一个题那样做,就会使最大值变成3,而不是1000。 这里
【基础教程】基于matlab局部特征检测与提取【1749期】
1 常见手工设计的低级别特征 语音:高斯混合模型和隐马尔可夫模型; Gabor features for : texture classification Local Binary Patterns (LBP) for:人脸识别 face classification. SIFT and HOG features for: 物体识别、行人检测object recognition. 2 局部特征与
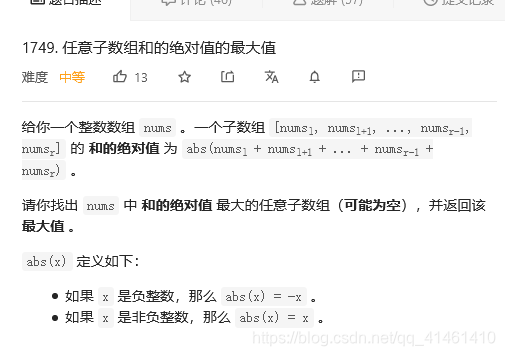
1749 任意子数组和的绝对值的最大值【leetcode每日一题系列】
采用前缀和维护数组,题目中子数组为连续的子序列,即求连续子序列中和的绝对值的最大值: result = 子序列中正数和 - 子序列中负数和 因此,要求result,只需要求子序列的最大正数和减去最小负数和。 定义sum变量表示前缀和,则数组nums的前缀和为: sum = nums[0]+nums[1]+nums[2]+...+nums[n]; 定义max变量表示前缀
Leetcode 1749. Maximum Absolute Sum of Any Subarray
文章作者:Tyan 博客:noahsnail.com | CSDN | 简书 1. Description 2. Solution **解析:**Version 1,分别求连续子数组的最大值与最小值,然后取二者绝对值较大的一个即可。 Version 1 class Solution:def maxAbsoluteSum(self, nums: List[int]) -> in
NOI / 2.1基本算法之枚举 1749:数字方格
描述: 如上图,有3个方格,每个方格里面都有一个整数a1,a2,a3。已知0 <= a1, a2, a3 <= n,而且a1 + a2是2的倍数,a2 + a3是3的倍数, a1 + a2 + a3是5的倍数。你的任务是找到一组a1,a2,a3,使得a1 + a2 + a3最大。 代码如下 #include<stdio.h>main(){int a1,a2,a3,max
LeetCode 1749. 任意子数组和的绝对值的最大值
题目 思路 这道题我在刚开始做时是想的动态规划的做法。考虑到已有和最大子数组的动态规划解法,本题要求绝对值最大的子数组,因此再维护一个以当前元素结尾的子数组和最小的数组,绝对值最大的数一定在和最大和和最小中产生。后来借鉴了其他大神的解法,这道题可以先求出前缀和数组,然后用其中的最大值和最小值相减即可(因为题目是求绝对值最大,因此不用考虑前缀和中减数和被减数的位置关系) class So
1749:数字方格 C
描述 如上图,有3个方格,每个方格里面都有一个整数a1,a2,a3。已知0 <= a1, a2, a3 <= n,而且a1 + a2是2的倍数,a2 + a3是3的倍数, a1 + a2 + a3是5的倍数。你的任务是找到一组a1,a2,a3,使得a1 + a2 + a3最大。 输入 一行,包含一个整数n (0 <= n <= 100)。 输出 一个整数,即a1 + a2 + a3的最大值。