欧拉φ函数的值 　通式：φ(x)=x(1-1/p1)(1-1/p2)(1-1/p3)(1-1/p4)…..(1-1/pn),其中p1, p2……pn为x的所有质因数，x是不为0的整数。φ(1)=1（唯一和1互质的数(小于等于1)就是1本身）。 (注意：每种质因数只一个。比如12=2*2*3  欧拉公式 那么φ（12）=12*（1-1/2）*(1-1/3)=4 若n是质数p的k次幂，φ(n)=p^k

一.题目链接： UVA-1395 二.题目大意： 给定 n 个点，m 条边的无向图. 定义生成树的 “苗条度” == max树边权值 - min树边权值. 求生成树的最小苗条度. 三.分析： 大体思路就是用 Kruskal 算法求解最小生成树. 由于生成树的 “苗条度” == max树边权值 - min树边权值 所以先 sort 一遍边的权值 然后从小到大枚举生成树的最小权值边

2^x mod n = 1 题目链接 2^x mod n = 1 题目大意     找到一个最小的x满足 2x mod n = 1 2^x\ mod\ n\ =\ 1如果没有则输出 2? mod n = 1 2^?\ mod\ n\ =\ 1 题解     我们可以把式子化为 (2∗2x−1) mod n = 1 (2*2^{x-1})\ mod\ n\ =\ 1 首先可以

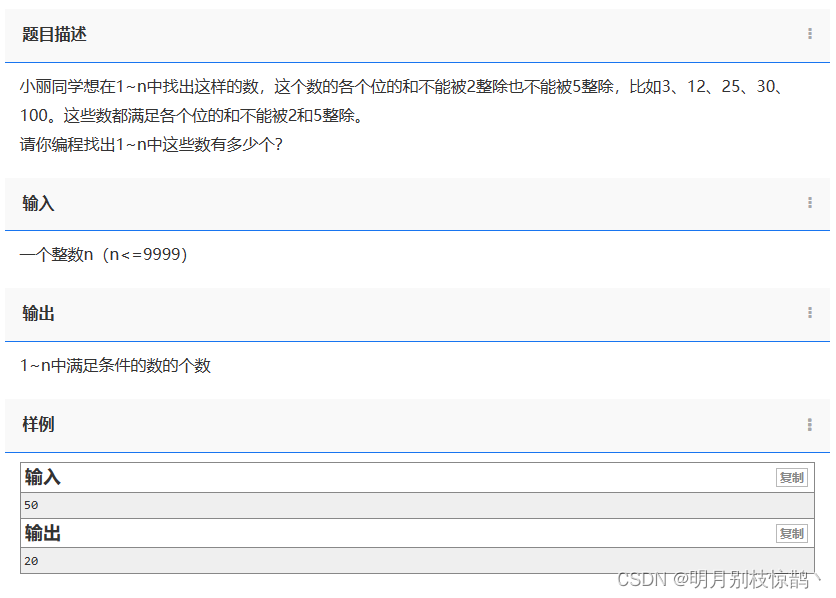
问题 小丽同学想在1~n中找出这样的数，这个数的各个位的和不能被2整除也不能被5整除，比如3、12、25、30、100。这些数都满足各个位的和不能被2和5整除。 请你编程找出1~n中这些数有多少个？ 1.分析问题 已知：1~n的数未知：满足各个数位的和sum不能被2和5整除的数关系：sum % 2 != 0 && sum % 5 != 0 2.定义变量 //二、数据定义 int n,

这个题  思路是比较简单。 但是自己在写的时候  由于 并查集 用的不熟  所以还是导致 超时 没写出来。 就去借鉴了一下别人的并查集用法。 并查集无非就是 将一个 集合 建成一棵树 这个集合 以跟节点为代表元素。 代表这个集合。 在搜的时候  如果判断这两个数是否在一个联通分量上 就直接查一下 是否 有同一个根节点 即可。 那么在这个题 在枚举 左端点 的时候每次

策略 ： 观察可知，1 或者是能被2整除的数都不会求余等于1， 只需要判断一下是不是除1之外的奇数，在依次查找2^x（mod（n）） ?= 1就可以了 难点：如果每次都是在原来的基础上×2 再判断 会超时。这时候，要用一下同余定理就可以了 AC by SWS; 题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=1395 代码： #include

目录 1. 解法一：枚举中点 2. 解法二：树状数组 + 离散化 优化解法一 原题链接：1395. 统计作战单位数 - 力扣（LeetCode） 题目描述： n 名士兵站成一排。每个士兵都有一个 独一无二 的评分 rating 。 每 3 个士兵可以组成一个作战单位，分组规则如下： 从队伍中选出下标分别为 i、j、k 的 3 名士兵，他们的评分分别为 rating[i]、r